2.3: Cram's Rule and Prelog's Rule
- Page ID
- 21833
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A carbonyl carbon is sp2 hybridized. This means that the carbonyl carbon and the three other atoms attached to it would be in one plane. A nucleophile attacking the carbonyl carbon in molecules like 1A in Figure 1.2.1 could attack from either side of this plane with equal ease. Have a close look at the aldehyde shown in Figure 1.2.1.The phenyl group is also flat. Nucleophilic attack on benzaldehyde could take place from either side with equal ease. Since a new asymmetric center is now created by this reaction, both enantiomers could be formed with equal ease, resulting in a racemic mixture.
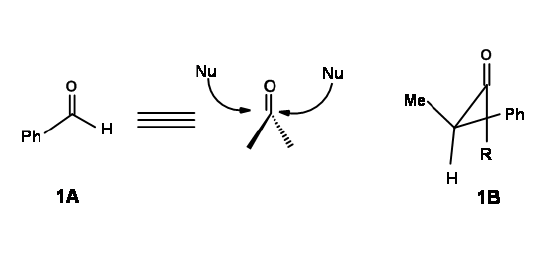
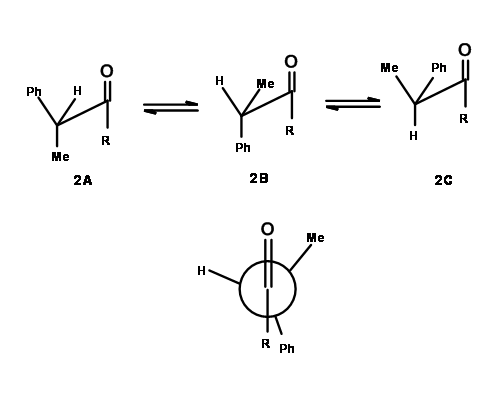
In complex organic molecules, this seldom happens. When the \(\alpha\) - carbon is asymmetric (see 1B), the nucleophile would experience more steric hindrance from one side, leading to unequal synthesis of the two enantiomers. This fact was first recognized by D. Cram in 1952. After analyzing several published reactions, he put forth an explanation based on one proposed conformation. He set forth to first define a Reactive conformation, as the least energy conformation in which the chemical reaction takes place. Thus, for 1B there could be several conformations, out of which chemical reactions prefer to proceed via the conformation having the least steric strain (Fig 1.2.2).
Studies in Stereochemistry. X. The Rule of "Steric Control of Asymmetric Induction" in the Syntheses of Acyclic Systems Donald J. Cram, Fathy Ahmed Abd Elhafez, J.Am. Chem. Soc. 74, 5828(1952).
Cram's Rule
- The existing asymmetric center would have a Small, Medium and Large group, denoted S,M and L respectively.
- In the reactive conformation, the carbonyl group would orient itself in such a way that it will rest between the Small group and the Medium group.
- The attacking nucleophile would prefer to attack from the side of the small group, resulting in the predominant formation of one diastereomer in the product.
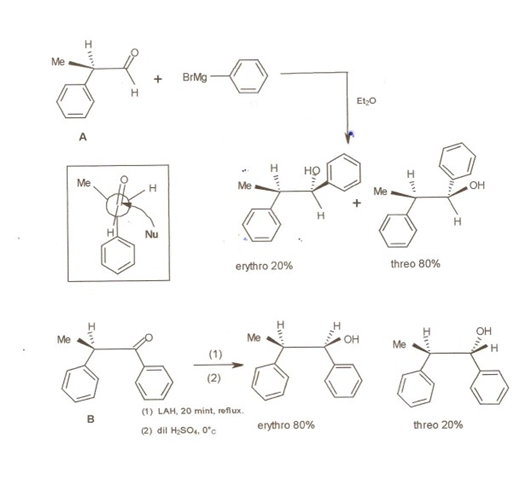
This is now known as Cram's Rule. When the starting material is a pure enantiomer, the product mixture would show predominance of one enantiomer. He supported his argument with a set of his own experiments shown in Figure 1.2.3
The predominance of one diastereomer in such reactions could be explained on the basis of Cram's Rules. This rule proved to be effective in predicting the major product in most of the asymmetric syntheses. However, several exceptions were soon observed. They were explained on the basis of further conformational arguments.
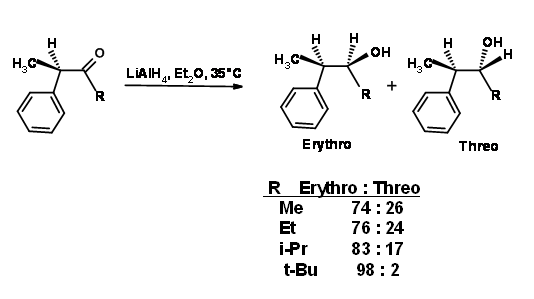
Felkin pointed out that the reactive conformations of Cram had severe eclipsing strain between R group on carbonyl center and L group on the  - carbon (see 2B in Figure 1.2.2). He progressively increased the bulk of the R group and observed that the diastereomeric excess could swing from erythro 74% to threo 96% as the bulk increased (Fig 1.2.4).
- carbon (see 2B in Figure 1.2.2). He progressively increased the bulk of the R group and observed that the diastereomeric excess could swing from erythro 74% to threo 96% as the bulk increased (Fig 1.2.4).
Torsional strain involving partial bonds. The stereochemistry of the lithium aluminium hydride reduction of some simple open-chain ketones. Marc Cherest, Hugh Felkin and Nicole Prudent Tetrahedron Letters, 9, 2199 (1968).
He proposed a staggered conformation, wherein the nucleophile approached the carbonyl carbon from the least hindered side. The major difference in these two approaches is depicted in Figure 1.2.5.
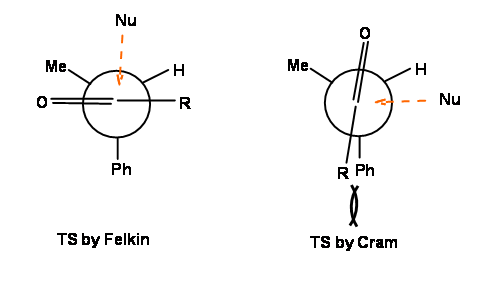
Figure 1.2.5
The flaw in the Felkin's model is that it is not true for aldehydes, where R=H. An improvement over Felkin's model was the Felkin-Nguyen (Felkin-Anh) model, which suggested that the nucleophile would attack the sp2 center of the carbonyl at 950 to 1050 angle relative to the carbonyl bond axis, favoring an attack from the least hindered direction (Figure 1.2.6). This differed from the earlier models that suggested a perpendicular attack.
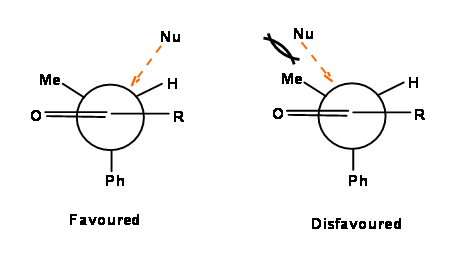
Figure 1.2.6
What happens when the  - carbon bears atoms like 'O','N' or 'S'? The first thought would be that the nucleophile would prefer the side opposite to the electronegative group. This would lead to a Felkin-Anh transition state. This would be true only when the reagent does not have additional complexing site. For example, in sodium borohydride the sodium ion cannot from a bivalent complex. On the other hand, zinc borohydride could form a divalent chelation complex between the carbonyl oxygen and the electronegative atom. This is called Cram-chelation complex, which leads to a Cram-chelate product. The three arguments discussed so far are shown in Figure 1.2.7.
- carbon bears atoms like 'O','N' or 'S'? The first thought would be that the nucleophile would prefer the side opposite to the electronegative group. This would lead to a Felkin-Anh transition state. This would be true only when the reagent does not have additional complexing site. For example, in sodium borohydride the sodium ion cannot from a bivalent complex. On the other hand, zinc borohydride could form a divalent chelation complex between the carbonyl oxygen and the electronegative atom. This is called Cram-chelation complex, which leads to a Cram-chelate product. The three arguments discussed so far are shown in Figure 1.2.7.
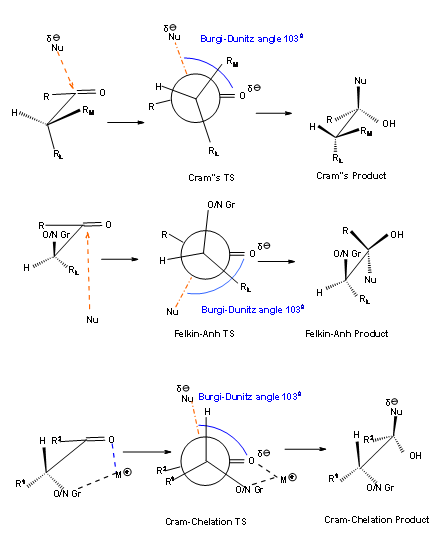
Figure 1.2.7
Two examples are shown in Figure 1.2.8 to depict that Cram's chelation control could lead to a reversal in selectivity. Notwithstanding these refinements to the original Crams's Rule, the fact remains that this line of extending conformational arguments to reactive conformations suggested by Cram has resulted in greater understanding of nucleophilic additions to aldehydes and ketones.
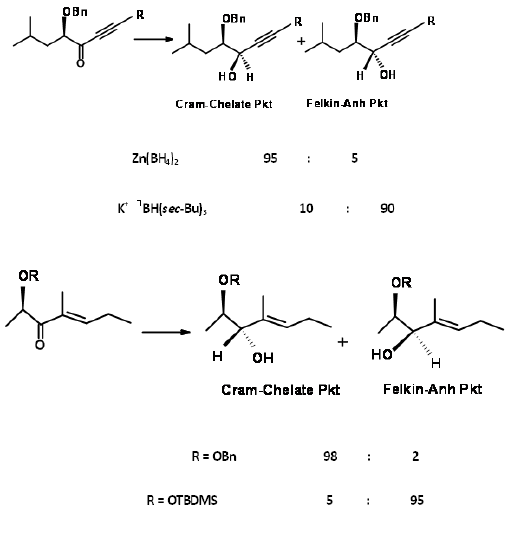
Figure 1.2.8
Prelog's Rule
An extension of Cram's idea of reactive conformation to chiral esters of \(\alpha\)-ketoesters(pyruvates) is the Prelog's Rule reported in 19533. It generally relates to Grignard addition to chiral pyruvates made using chiral alcohols (Fig 1.2.9).
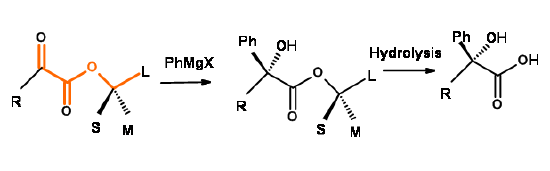
Figure 1.2.9
The rule has been applied for asymmetric synthesis of \(\alpha\)-hydroxyacids and for assigning the configuration of secondary and tertiary alcohols. The anti configurational arrangement of the two \(\alpha\)-carbonyl moieties could be rationalized. The negative end of these dipoles would prefer to be as far removed as possible. The two lone pairs would sit on ether oxygen like the 'Rabit Ears'. The keto-carbonyl would orient between the two ears. This will place the bonds shown in red in the same plane as thr keto-carbonyl group. The attack from the side of the small (S) group is an extension of Cram's Rules. The asymmetric induction could be at times poor due to the large distance between the reaction center and the asymmetric center inducing asymmetry at the developing chiral center.
References
- Prelog V, Helv. Chim. Acta, 36, 308(1953)


