2.1: Baldwin’s Rule for Ring Closure Reactions
- Page ID
- 21826
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)J.E. Baldwin proposed a set of rules for ring closure reactions. He suggested that the rules are applicable to reactive intermediates as well and supported his views with several examples from literature and special experiment designed to test the validity of the rules.
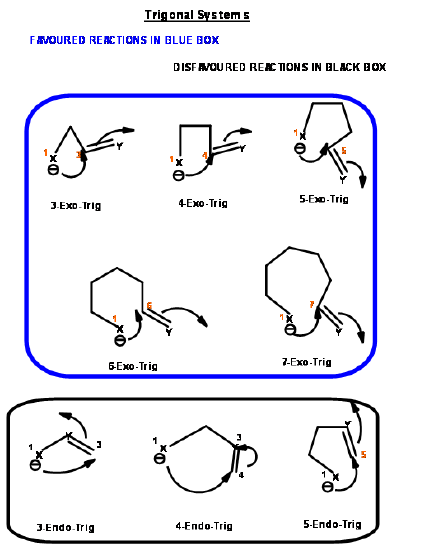
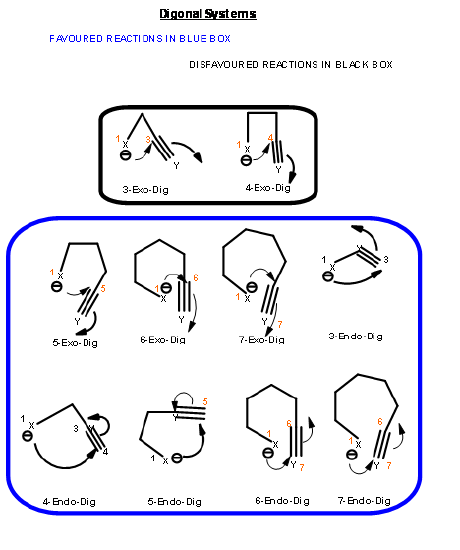
The ring closure reaction of a reactive intermediate could be one of the three types. An attack could be on a triple bond center (called Digonal center, Dig-), a double bond center (called Trigonal center, Trig-) or at a single bond center (called Tetrahedral center, Tet-). The attacking species could be a carbanion, a carbonium ion or a free radical. The attack could be endo- or exo-. With respect to the newly developing ring in the transition state, when the pair of electrons in the displaced bond is exo- to the developing ring, the transition state is described as exo- attack. When they form part of the newly developing ring (or transition state) the system is described as endo- attack (Fig 2.2.1).
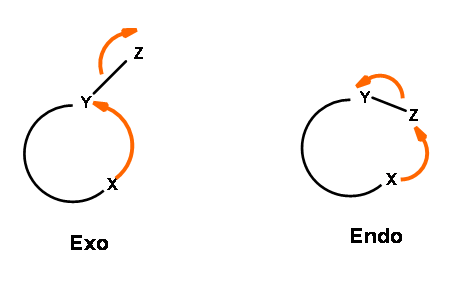
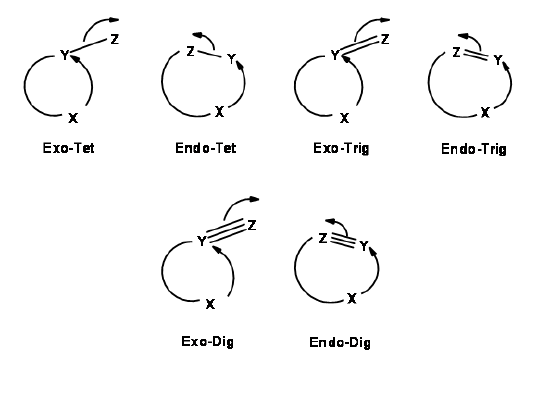
For each pair of reactive center, there could be two modes of attack – endo- or exo- as shown for the attack of an anion (Fig 2.2.2).
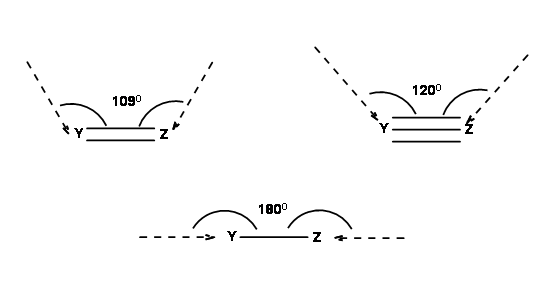
Reactions take place only when the orbitals concerned overlap efficiently. For this purpose, Baldwin suggested the following geometry (Fig 2.2.3). In a ring formation reaction, the optimal geometry could be achieved only when the length of the chain (a tether of atoms) connecting the reactive centers have a minimum optimal length.
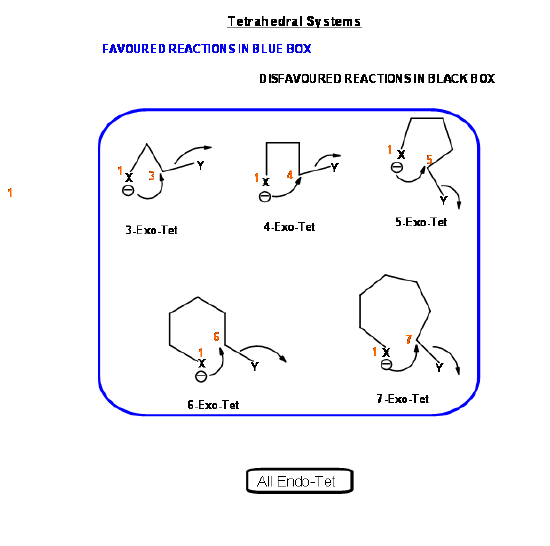
Based on this criterion, Baldwin suggested the following rules. The number (3 to 7) in the nomenclature refers to the number of atoms in the chain that leads to the proposed cyclic transition state.
Baldwins Rules
- All Exo-Tet reactions are favored reactions
- All Endo-Tet are disfavored reactions
- All Exo-Trig reactions are favored reactions
- 3 to 5-Endo-Trig reactions are disfavored reactions
- 6 and 7-Endo-Trig reactions are favored reactions
- 3 to 7-Endo-Dig reactions are favored reactions
- 3 to 4-Exo-Dig reactions are disfavored reaction
- 5 to 7-Exo-Dig are favored reactions
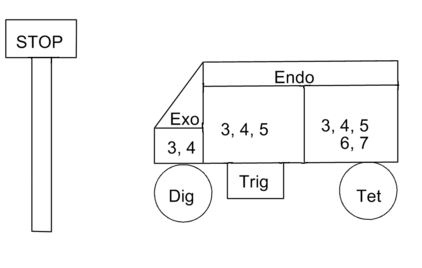
These complex rules are simple to apply, but difficult to remember without a suitable ‘memory aid’. E. Juaristi 2 (in his web page http://www.relaq.mx/RLQ/EusebioJuaristi_vitae.htm) suggests the following mnemonics for all the Disfavored Reactions (the Stop sign). A modified version is presented here (Fig 2.2.4). Note that the numbers are progressively increasing. The STOP sign and the wagon would probably be easier to remember.
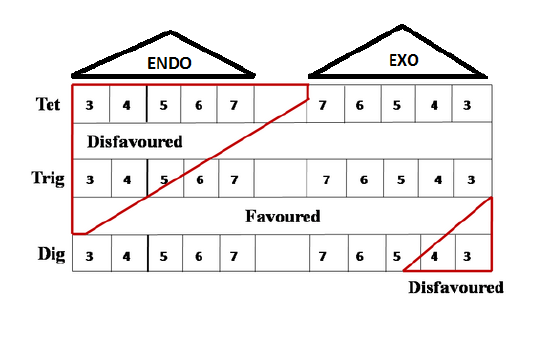
An alternate summary of the Baldwin’s Rules is provided by Clayden et. al., in their inimitable text book. This table is now easy to remember (Fig 2.2.5). You have to remember 5-Endo-trig and 4-Exo-Dig as key points for Disfavored reactions.
Baldwin cited several examples in support of these rules. Scientists soon attempted to validate the proposed rules. Steric and electronic factors appear to modify these conclusions. In most of the studies, the rules were generally applicable. Let us look at the following interesting study (Fig 2.2.6). A 6-endo-Tet reaction should be disfavored. Such reactions do not form a ring, but appear to pass through a cyclic transition state leading to the cleavage of a sigma bond, while a new sigma bond is formed.
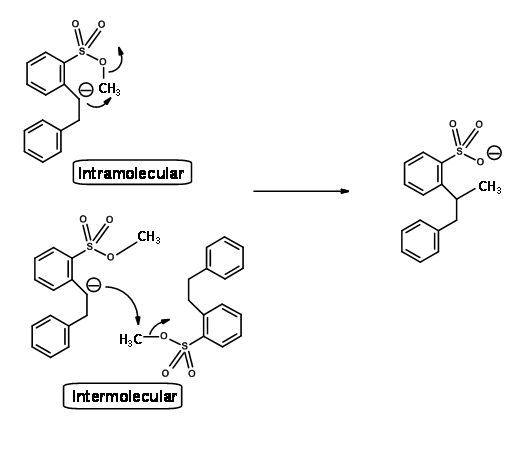
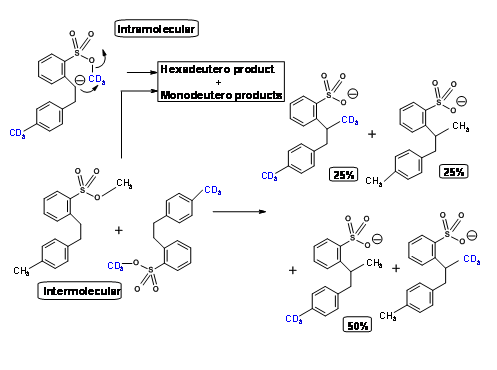
Using an ingenious double labeling experiment shown below, Eschenmoser clearly established that this reaction is intermolecular (Fig 2.2.7). He took an equimolar mixture of hexadeutero- and normal starting materials and conducted the reaction. If the reaction were only intramolecular, the product would be both hexadeutero- and no deutero- products only. The actual product distribution was as shown in Figure 2.2.7, which is in keeping with intermolecular mechanism only.
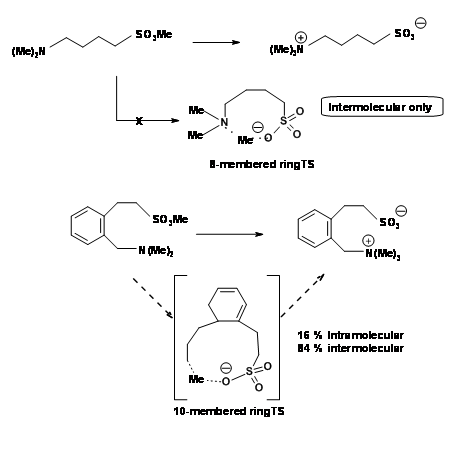
The constraint in such cases lies obviously in the length of the chain bearing the reactive groups. The angle of attack of 1800 is not attainable in a six-membered ring. King et al.,showed that as the length of the chain (tether) increased, intramolecular reaction became more feasible as shown in Figure 2.2.8. An intramolecular reaction became feasible only when the teather allowed a ten-membered ring transition state.
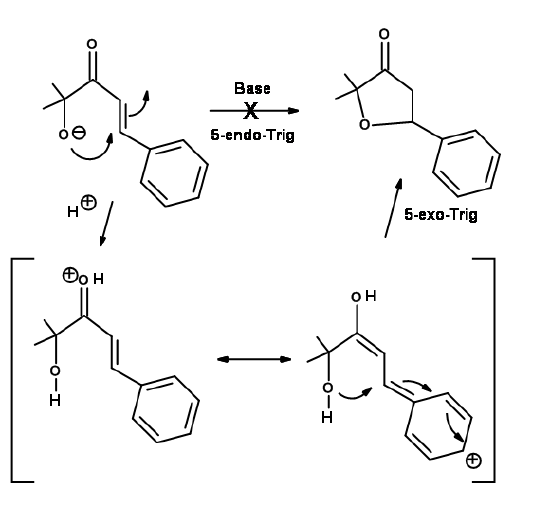
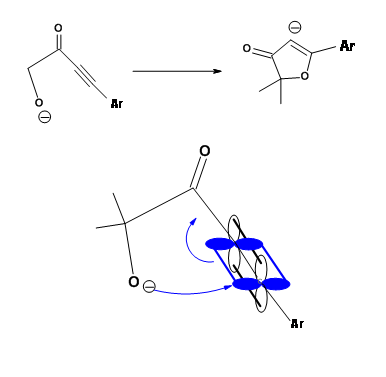
Another Disfavored cyclization is 5-Endo-Trig. The following Michael-type cyclization is of considerable interest (Fig 2.2.9). The base catalyzed intramolecular addition does not proceed as expected. However, the acid catalyzed reaction proceeds. A close look at an alternate mechanism suggests that a 5-Exo-Trig path becomes available under acid catalyzed conditions .
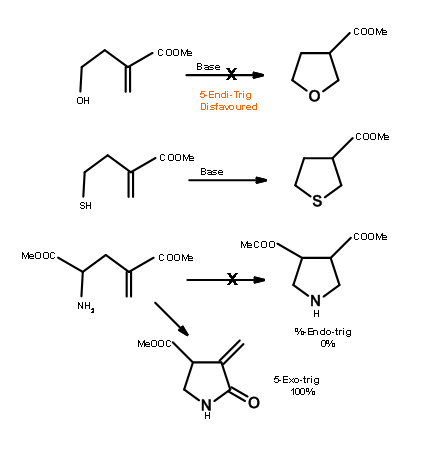
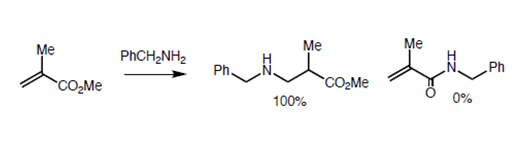
Baldwin sites three closely related reactions (Fig 2.2.10) to support his rules. The oxygen analogue failed to cyclize as anticipated for 5-Endo-Trig reactions. However, the thiol analogue cyclized readily to give the thiophene ring. This is attributed to the fact that the larger atom requires entirely different bond angles not envisaged in Baldwin’s Rules. The nitrogen analogue investigated preferred an alternate path. Why does the nitrogen prefer amidation and not Michael-type cyclization? Could it be due to an unreactive olefin? This question was answered through an intermolecular ‘control reaction’ shown in Fig 2.2.11. The amine moiety preferred a Michael-type addition to amidation.
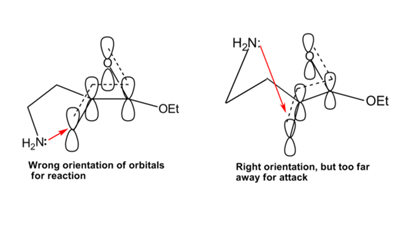
This lack of cyclization was therefore attributed to the fact that the lone pair cannot attack the pi-orbitals due to wrong orientation in one conformation and the distances involved in the other conformation (see Figure 2.2.12).
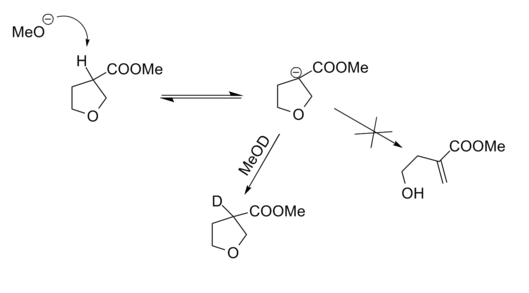
Applicability of Baldwin’s 5-Endo-Trig restriction was verified through a carefully planned retro-reaction (Fig 2.2.13). The Deuterium labeling experiment proved the fact that anion formation was effective. Lack of cleavage reaction proved that the above conclusions (5-Endo-Trig restriction) are valid in reverse reactions as well.
The fact that 5-Exo-Trig is favored is seen in several reactions. The fact that 6-Endo-Trig reactions are favored is also well documented (Fig 2.2.14).
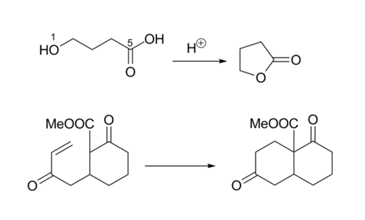
The 5-Endo-Dig cyclization looks awkward on paper (Fig 2.2.15). But the reaction proceeds to completion. A close look at the orbitals concerned explains the reaction. The orientation of one of the pi-orbitals is just right for the reaction to occur. Compare this with the orientation shown in Figure 2.2.12.
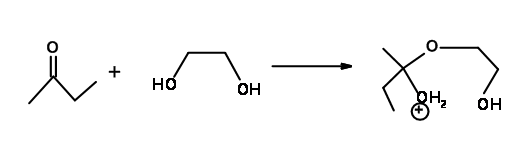
How about the acetal formation reaction of ketones with ethylene glycol (Fig 2.2.16)? Is this a case of failure of Baldwin’s Rules as in several carbonium ion reactions?
These rules are generally applicable. However, there are several exceptions as well. A proper approach would be to use these ‘thumb rules’ as a guideline while planning synthetic schemes and not use them as inviolable rules. The following points may be kept in mind while applying these rules.
1. The rules suggest only the ‘favored paths’. This expression ‘favored / disfavored’ should not be read as ‘allowed / disallowed’. Under suitable conditions, the alternate high-energy path may be opened, either partially or exclusively.
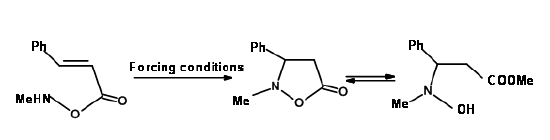
2. When a large atom from the Second Group of the periodic table is involved, the angle requirements of these atoms may vary. In such cases, the rules may not be applicable. See Fig 2.2.10 for one such example.
3. Special modified Baldwin’s Rules have been evolved for enolate anions.
References
- J.E. Baldwin, J. Chem. Soc., Chem. Commun.,734 (1976). J.E. Baldwin, J. Cutting, W. Dupond, L. Kruse, L. Silberman, R.C. Thomas, J. Chem. Soc., Chem. Commun.,736 (1976). J.E. Baldwin, R.C. Thomas, L. Kruse, L. Silberman, J. Org. Chem., 42, 3846 (1977). J.E. Baldwin, L. Kruse, J. Chem. Soc., Chem. Commun., 233 (1977). J.E. Baldwin, M.J. Lusch, Tetrahedron, 38, 2939 (1982). C.D.Johnson, Acc. Chem. Res., 26, 476 (1993).
- Eusebio Juaristi and Gabriel Cuevas, Rev. Soc. Quím. Méx, 36, 48 (1992)
- Organic Chemistry by Clayden, Greeves, Warren and Wothers: Page 1144.
- Eschenmoser. Helv. Chim.. Acta., 53, 2059 (1970)
- King et. al., Chem. Commun., 175 (1982); Tetrahedron Lett., 23, 4465 (1982). and Peter Beak, Acc. Chem. Rec., 25, 215 (1992).


