4.2: Theory

Objectives

After completing this section, you should be able to

• identify (by wavelength, wavenumber, or both) the region of the electromagnetic spectrum which is used in infrared (IR) spectroscopy.
• discuss, in general terms, the effect that the absorption of infrared radiation can have on a molecule.

Infrared (IR) spectroscopy is one of the most common and widely used spectroscopic techniques employed mainly by inorganic and organic chemists due to its usefulness in determining structures of compounds and identifying them. Chemical compounds have different chemical properties due to the presence of different functional groups.

Introduction

Absorbing groups in the infrared region absorb within a certain wavelength region. The absorption peaks within this region are usually sharper when compared with absorption peaks from the ultraviolet and visible regions. In this way, IR spectroscopy can be very sensitive to determination of functional groups within a sample since different functional group absorbs different particular frequency of IR radiation. Also, each molecule has a characteristic spectrum often referred to as the fingerprint. A molecule can be identified by comparing its absorption peak to a data bank of spectra, which will be discussed in detail in other sections. IR spectroscopy is very useful in the identification and structure analysis of a variety of substances, including both organic and inorganic compounds. It can also be used for both qualitative and quantitative analysis of complex mixtures of similar compounds.

The use of infrared spectroscopy began in the 1950's by Wilbur Kaye. He had designed a machine that tested the near-infrared spectrum and provided the theory to describe the results. Karl Norris started using IR Spectroscopy in the analytical world in the 1960's and as a result IR Spectroscopy became an accepted technique. There have been many advances in the field of IR Spectroscopy, the most notable was the application of Fourier Transformations to this technique thus creating an IR method that had higher resolution and a decrease in noise. The year this method became accepted in the field was in the late 1960's.

Absorption Spectroscopy

There are three main processes by which a molecule can absorb radiation and each of these routes involves an increase of energy that is proportional to the light absorbed. The first route occurs when absorption of radiation leads to a higher rotational energy level in a rotational transition. The second route is a vibrational transition which occurs on absorption of quantized energy. This leads to an increased vibrational energy level. The third route involves electrons of molecules being raised to a higher electron energy, which is the electronic transition. It’s important to state that the energy is quantized and absorption of radiation causes a molecule to move to a higher internal energy level. This is achieved by the alternating electric field of the radiation interacting with the molecule and causing a change in the movement of the molecule. There are multiple possibilities for the different possible energy levels for the various types of transitions.

The energy levels can be rated in the following order: electronic > vibrational > rotational. Each of these transitions differs by an order of magnitude. Rotational transitions occur at lower energies (longer wavelengths) and this energy is insufficient and cannot cause vibrational and electronic transitions but vibrational (near infra-red) and electronic transitions (ultraviolet region of the electromagnetic spectrum) require higher energies.

Figure 1: Energy levels for a molecule. Possible transitions that occur: (A): Pure rotational Transitions, (B) rotational-Vibrational Transitions, (C) Rotational-Vibrational-Electronic Transitions

The energy of IR radiation is weaker than that of visible and ultraviolet radiation, and so the type of radiation produced is different. Absorption of IR radiation is typical of molecular species that have a small energy difference between the rotational and vibrational states. A criterion for IR absorption is a net change in dipole moment in a molecule as it vibrates or rotates. Using the molecule HBr as an example, the charge distribution between hydrogen and bromine is not evenly distributed since bromine is more electronegative than hydrogen and has a higher electron density. \(HBr\) thus has a large dipole moment and is thus polar. The dipole moment is determined by the magnitude of the charge difference and the distance between the two centers of charge. As the molecule vibrates, there is a fluctuation in its dipole moment; this causes a field that interacts with the electric field associated with radiation. If there is a match in frequency of the radiation and the natural vibration of the molecule, absorption occurs and this alters the amplitude of the molecular vibration. This also occurs when the rotation of asymmetric molecules around their centers results in a dipole moment change, which permits interaction with the radiation field.

Diatomic Molecular Vibration

The absorption of IR radiation by a molecule can be likened to two atoms attached to each other by a massless spring. Considering simple diatomic molecules, only one vibration is possible. The Hook's law potential on the other hand is based on an ideal spring

\[\begin{align} F &= -kx \label{1} \\[4pt] &= -\dfrac{dV(x)}{dx} \label{2} \end{align}\]

this results in one dimensional space

\[ V(r) = \dfrac{1}{2} k(r-r_{eq})^2 \label{3}\]

One thing that the Morse and Harmonic oscillator have in common is the small displacements (\(x=r-r_{eq}\)) from the equilibrium. Solving the Schrödinger equation for the harmonic oscillator potential results in the energy levels results in

\[ E_v = \left(v+\dfrac{1}{2}\right)hv_e \label{4}\]

with \(v=0,1,2,3,...,\,infinity\)

\[ v_e = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{\mu}} \label{5}\]

When calculating the energy of a diatomic molecule, factors such as anharmonicity (has a similar curve with the harmonic oscillator at low potential energies but deviates at higher energies) are considered. The energy spacing in the harmonic oscillator is equal but not so with the anharmonic oscillator. The anharmonic oscillator is a deviation from the harmonic oscillator. Other considered terms include; centrifugal stretching, vibrational and rotational interactions have to be taken into account. The energy can be expressed mathematically as

\[ E_v = \underset{\text{Harmonic Oscillator}}{\left(v+\dfrac{1}{2}\right)hv_e} - \underset{\text{anharmonicity}}{\left(v+\dfrac{1}{2}\right)^2 X_e hv_e} + \underset{\text{Rigid Rotor}}{B_e J (J+1)} - \underset{\text{centrifugal stretching}}{D_e J^2 (J+1)^2} -\alpha_e \underset{\text{rovibrational coupling}}{\left(v+\dfrac{1}{2}\right) J(J+1)} \label{6}\]

The first and third terms represent the harmonicity and rigid rotor behavior of a diatomic molecule such as HCl. The second term represents anharmonicity and the fourth term represents centrifugal stretching. The fifth term represents the interaction between the vibration and rotational interaction of the molecule.

Polyatomic Molecular Vibration

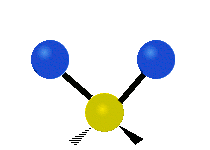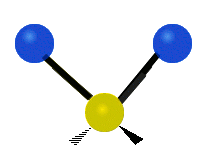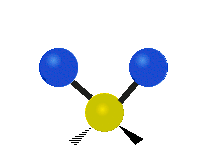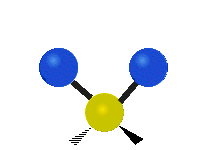
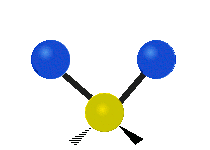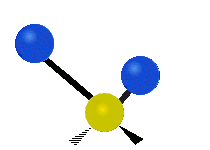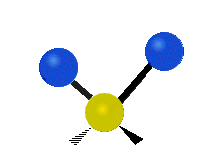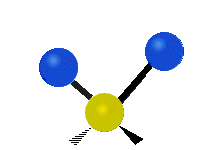
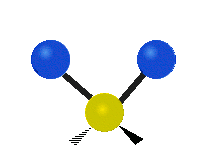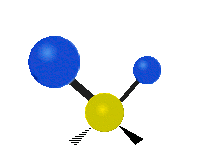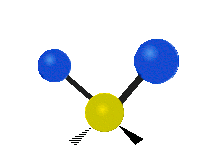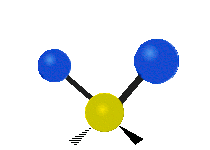
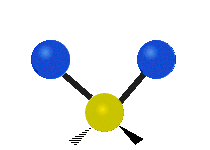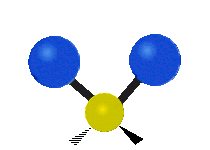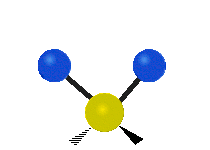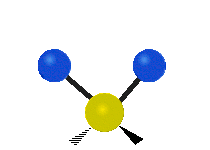
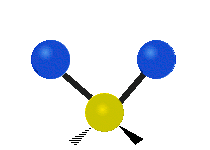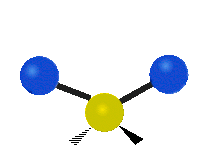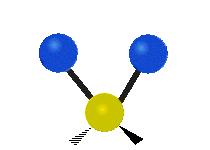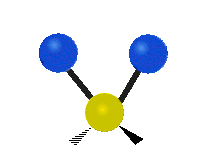
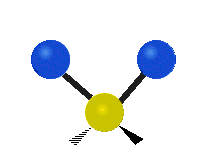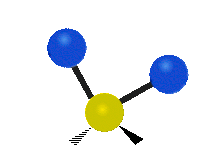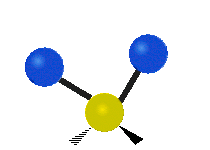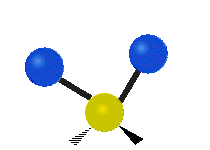
The bond of a molecule experiences various types of vibrations and rotations. This causes the atom not to be stationary and to fluctuate continuously. Vibrational motions are defined by stretching and bending modes. These movements are easily defined for diatomic or triatomic molecules. This is not the case for large molecules due to several vibrational motions and interactions that will be experienced. When there is a continuous change in the interatomic distance along the axis of the bond between two atoms, this process is known as a stretching vibration. A change in the angle occurring between two bonds is known as a bending vibration. Four bending vibrations exist namely, wagging, twisting, rocking and scissoring. A CH₂ group is used as an example to illustrate stretching and bending vibrations below.

Symmetric Stretch Asymmetric Stretch Twisting

Wagging Scissoring Rocking

Types of Vibrational Modes. To ensure that no center of mass motion occurs, the center atom (yellow ball) will also move. Figure from Wikipedia

As stated earlier, molecular vibrations consist of stretching and bending modes. A molecule consisting of (N) number of atoms has a total of 3N degrees of freedom, corresponding to the Cartesian coordinates of each atom in the molecule. In a non-linear molecule, 3 of these degrees of freedom are rotational, 3 are translational and the remainder is fundamental vibrations. In a linear molecule, there are 3 translational degrees of freedom and 2 are rotational. This is because in a linear molecule, all of the atoms lie on a single straight line and hence rotation about the bond axis is not possible. Mathematically the normal modes for a linear and non linear can be expressed as

Linear Molecules: (3N - 5) degrees of freedom

Non-Linear molecules: (3N - 6) degrees of freedom

Example 1: Vibrations of Water

Diagram of Stretching and Bending Modes for H₂O.

Solution

H₂O molecule is a non-linear molecule due to the uneven distribution of the electron density. O₂ is more electronegative than H₂ and carries a negative charge, while H has a partial positive charge. The total degrees of freedom for H₂O will be 3(3)-6 = 9-6 = 3 degrees of freedom which correspond to the following stretching and bending vibrations. The vibrational modes are illustrated below:

The vibrational modes of H₂O

Example Vibrations of \(CO_2\)

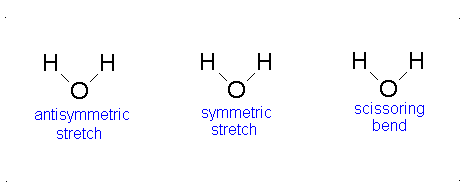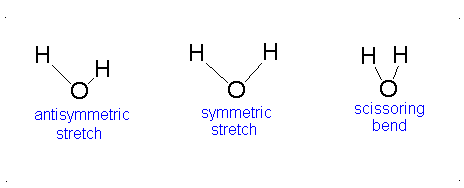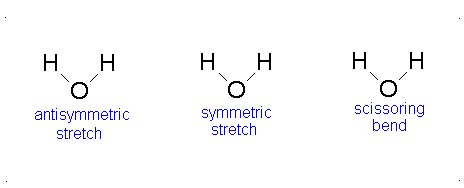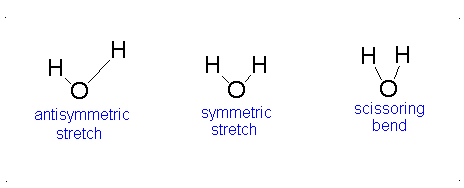
Diagram of Stretching and Bending Modes for CO₂.

Solution

CO₂ is a linear molecule and thus has the formula (3N-5). It has 4 modes of vibration (3(3)-5). CO₂ has 2 stretching modes, symmetric and asymmetric. The CO₂ symmetric stretch is not IR active because there is no change in dipole moment because the net dipole moments are in opposite directions and as a result, they cancel each other. In the asymmetric stretch, O atom moves away from the C atom and generates a net change in dipole moments and hence absorbs IR radiation at 2350 cm^-1. The other IR absorption occurs at 666 cm^-1. CO₂ symmetry with \(D_{\infty h}\) CO₂ has a total of four of stretching and bending modes but only two are seen. Two of its bands are degenerate and one of the vibration modes is symmetric hence it does not cause a dipole moment change because the polar directions cancel each other. The vibrational modes are illustrated below:

The vibrational modes of CO₂

Selection Rules of IR

In order for vibrational transitions to occur, they are normally governed by some rules referred to as selection rules.

1. An interaction must occur between the oscillating field of the electromagnetic radiation and the vibrational molecule for a transition to occur. This can be expressed mathematically as

\(\left(\dfrac{d\mu}{dr}\right)_{r_{eq}} \not= 0 \label{30}\)

\(\triangle v = +1\) and \(\triangle J = +1 \label{31}\)

2. This holds for a harmonic oscillator because the vibrational levels are equally spaced and that accounts for the single peak observed in any given molecular vibration. For gases J changes +1 for the R branch and -1 for the P branch.\(\triangle J = 0\) is a forbidden transition and hence a q branch for a diatomic will not be present. For any anharmonic oscillator, the selection rule is not followed and it follows that the change in energy becomes smaller. This results in weaker transitions called overtones, then \(\triangle v = +2\) (first overtone) can occur, as well as the 2^nd overtone \(\triangle v = +3\). The frequencies of the 1^st and 2^nd overtones provides information about the potential surface and about two to three times that of the fundamental frequency.
3. For a diatomic, since \(\mu\) is known, measurement of u_e provides a value for k, the force constant.

\(k = \left(\dfrac{d^2 V(r)}{dr^2}\right)_{r_{eq}} \label{32}\)

where k is the force constant and indicates the strength of a bond.

Influence Factors of IR

• Isotope Effects: It's been observed that the effect on k when an atom is replaced by an isotope is negligible but it does have an effect on \(\nu\) due to changes in the new mass. This is because the reduced mass has an effect on the rotational and vibrational behavior.
• Solvent Effects: The polarity of solvent will have an influence on the IR spectra of organic compounds due to the interactions between solvent and compounds, which is called solvent effects. If we place a compound, which contains n, pi and pi* orbitals, into a polar solvent, the solvent will stabilizes these three orbitals in different extent. The stabilization effects of polar solvent on n orbital is the largest one, the next larger one is pi* orbital, and the effects on pi orbital is the smallest one. The spectra of n→pi* transition will shift to blue side, which means it will move to shorter wavelengths and higher energies since the polar solvent causes the energy difference between n orbital and pi* orbital to become bigger. The spectra of pi→pi* transition will shift to red side, which means it will move to longer wavelengths and lower energies since the polar solvent causes the energy difference between n orbital and pi* orbital to become smaller.

In summary, some bonds absorb infrared light more strongly than others, and some bonds do not absorb at all. In order for a vibrational mode to absorb infrared light, it must result in a periodic change in the dipole moment of the molecule. Such vibrations are said to be infrared active. In general, the greater the polarity of the bond, the stronger its IR absorption. The carbonyl bond is very polar, and absorbs very strongly. The carbon-carbon triple bond in most alkynes, in contrast, is much less polar, and thus a stretching vibration does not result in a large change in the overall dipole moment of the molecule. Alkyne groups absorb rather weakly compared to carbonyls. Some kinds of vibrations are infrared inactive. The stretching vibrations of completely symmetrical double and triple bonds, for example, do not result in a change in dipole moment, and therefore do not result in any absorption of light (but other bonds and vibrational modes in these molecules do absorb IR light).

Exercise \(\PageIndex{1}\)

Which of the three main processes a molecule can absorb radiation leads to IR absorptions? What 

Answer

Absorption of IR radiation is typical of molecular species that have a small energy difference between the rotational and vibrational states.

Exercise \(\PageIndex{2}\)

What is key for a molecule to be IR active?

Answer

A criterion for IR absorption is a net change in dipole moment in a molecule as it vibrates or rotates.

Exercise \(\PageIndex{3}\)

Define a stretching vibration.

Answer

In a stretching vibration, the distance between two atoms increases and decreases in a rhythmic manner, but the atoms remain aligned along the bond axis. 

Exercise \(\PageIndex{4}\)

Define a bending vibration.

Answer

In a bending vibration, the positions of the atoms change relative to the bond axis. 

Exercise \(\PageIndex{5}\)

What are the vibrational modes of the methylene group, CH₂?

Answer

The stretching and bending vibrations of methylene chloride are: 

• symmetric stretching
• asymmetric stretching
• wagging
• twisting
• rocking
• scissoring

Exercise \(\PageIndex{6}\)

The intensity of C=O stretching is stronger than that of C=C stretching. The C=O also appears at a higher wavenumber than a C=C. Explain it. 

Answer

The carbonyl bond is very polar, and absorbs very strongly. The carbon-carbon double bond in most alkenes, in contrast, is much less polar, and thus a stretching vibration does not result in a large change in the overall dipole moment of the molecule. Alkene groups absorb rather weakly compared to carbonyls.

A C=O bond is stronger than a C=C bond. Stronger bonds lead to a higher frequency absorbed due to Hooke's Law.  

References

1. D. A. Skoog, F. J. Holler, S. R. Crouch. Principles of Instrumental Analysis, 6th ed. Belmont, CA. Thomson Higher Education. 2007
2. G. D. Christain. Analytical Chemistry, 5th ed. New York. John Wiley & Sons, INC. 1994
3. R. S. Drago. Physical Methods, 2nd ed. Mexico.Saunders College Publishing.1992
4. S.M. Blinder. Introduction to Quantum Mechanics. Academic Press. 2004
5. D. C. Harris, M. D. Bertolucci. Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic Spectroscopy. New York. Dover Publications, INC