19.10: Asymmetric Synthesis

If one could prepare 2-hydroxypropanenitrile from ethanal and hydrogen cyanide in the absence of any chiral reagent and produce an excess of one enantiomer over the other, this would constitute an absolute asymmetric synthesis - that is, creation of preferential chirality (optical activity) in a symmetrical environment from symmetrical reagents:

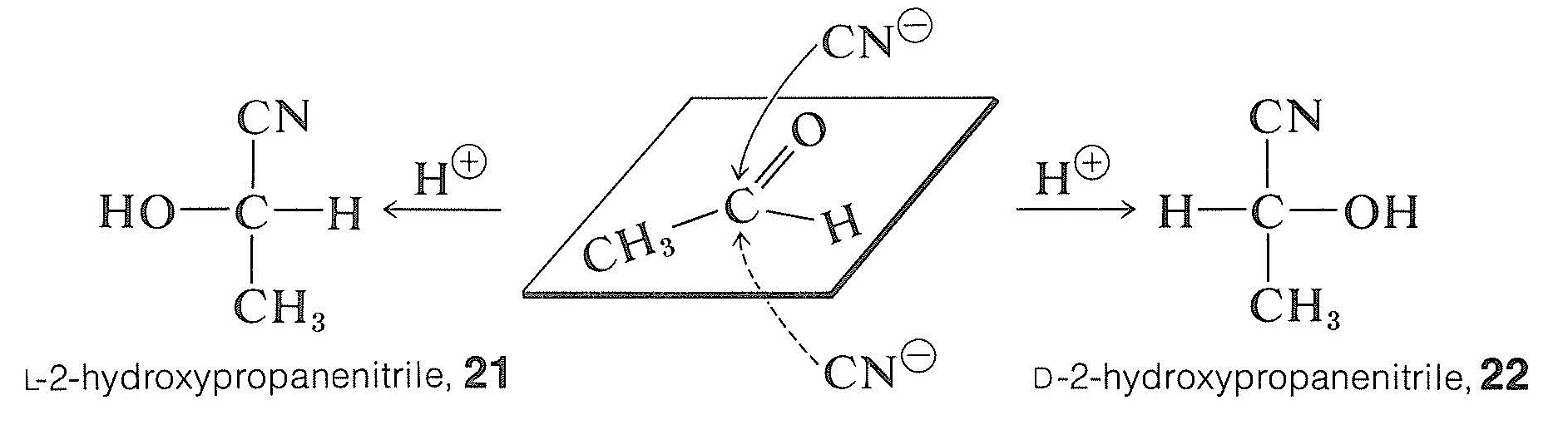
This obviously is unlikely for the given example because there is no reason for cyanide ion to have anything other than an exactly equal chance of attacking above or below the plane of the ethanal molecule, producing equal numbers of molecules of the enantiomers, \(21\) and \(22\). However, when a chiral center is created through reaction with a dissymmetric (chiral) reagent, we should not expect an exactly 1:1 mixture of the two possible isomers. For example, in an aldol-type addition (Section 18-8E) of a chiral ester to a prochiral ketone the two configurations at the new chiral center in the products \(23\) and \(24\) are not equally favored. That is to say, asymmetric synthesis is achieved by the influence of one chiral center \(\left( \ce{R}^* \right)\) on the development of the second:

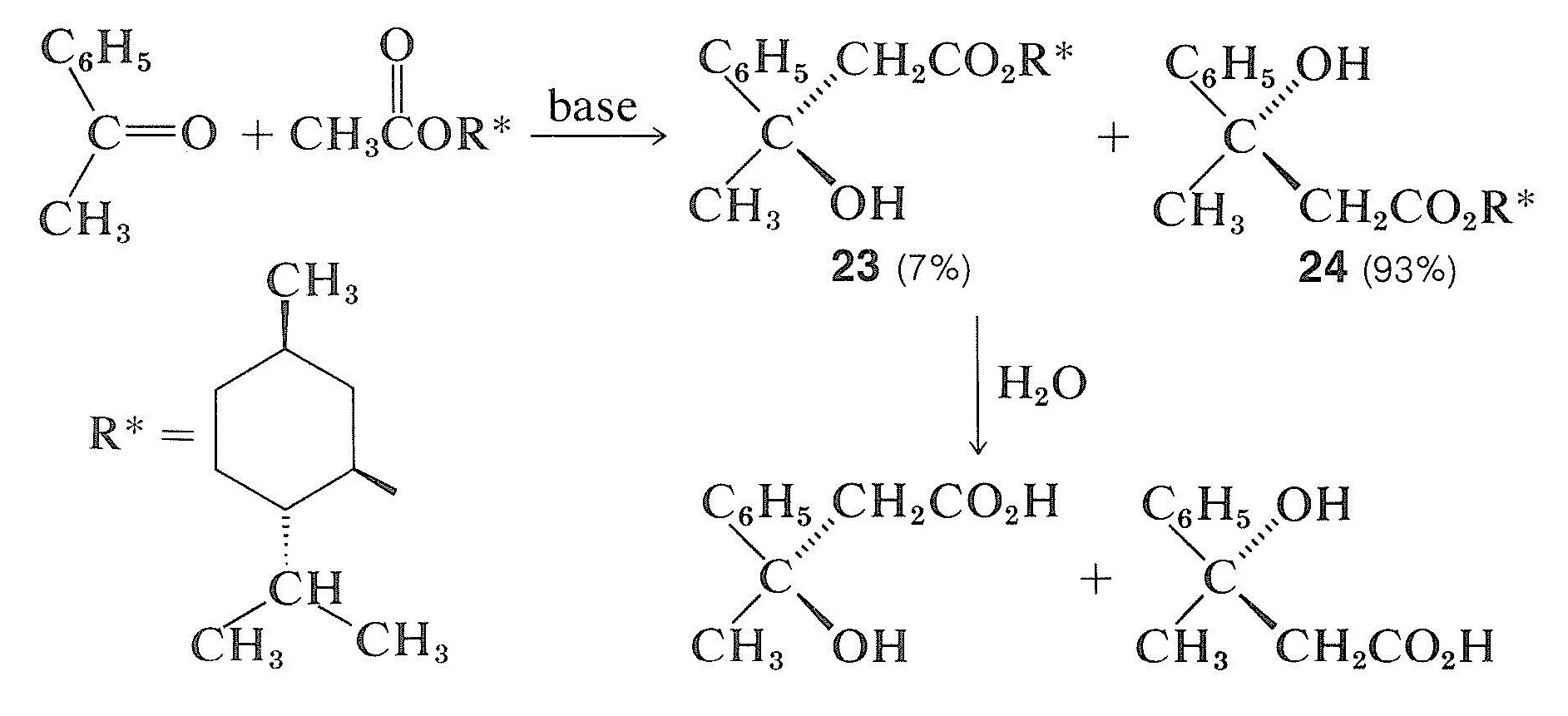
You will notice that the reaction products \(23\) and \(24\) are diastereomers, not enantiomers. Asymmetric synthesis can be achieved only when the possible transition states for reaction are diastereomeric because they then will have different energies and will lead to products at different rates. The larger the energy difference between diastereomeric transition states, the more stereochemical preference there will be for one chirality over the other.

The degree of stereochemical control displayed by the first chiral center usually depends on how close it is to the second - the more widely separated they are, the less steric control there is. Another factor is the degree of electronic control. If all the groups are very much the same electrically and sterically, not much stereochemical control is to be expected. Even when the chiral centers are close neighbors, asymmetric induction is seldom \(100\%\) efficient in simple molecules. In biochemical systems, however, asymmetric synthesis is highly efficient.

The stereospecificity of living organisms is imperative to their efficiency. The reason is that it is just not possible for an organism to be so constructed as to be able to deal with all of the theoretically possible isomers of molecules with many asymmetric centers. Thus a protein molecule not uncommonly has 100 or more different asymmetric centers; such a molecule would have \(2^{100}\) or \(10^{30}\) possible optical isomers. A vessel with a capacity on the order of \(10^7\) liters would be required to hold all of the possible stereoisomeric molecules of this structure if no two were identical. An organism so constituted as to be able to deal specifically with each one of these isomers would be very large indeed.

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."