19.9: Optical Rotatory Dispersion and Circular Dichroism
- Page ID
- 22781
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Optical rotations usually are measured at just one wavelength, namely \(589.3 \: \text{nm}\), simply because sodium-vapor lamps provide an especially convenient source of monochromatic light. Measurements at other wavelengths are less easily made without specialized instruments, with which relatively few laboratories are currently equipped. Nevertheless, much information has been obtained about structure, conformation, and configuration of organic compounds from measurements of optical rotation as a function of wavelength (i.e., optical rotatory dispersion).
Like other phenomena involving interactions between electromagnetic radiation and organic molecules, as in infrared, ultraviolet, and nmr spectroscopy, optical rotatory dispersion curves often are quite sensitive to small changes in structure. As an example, the rotatory dispersion curves for enantiomers of cis- and trans-10-methyl-2-decalones, \(16\) and \(17\), are reproduced in Figure 19-7:
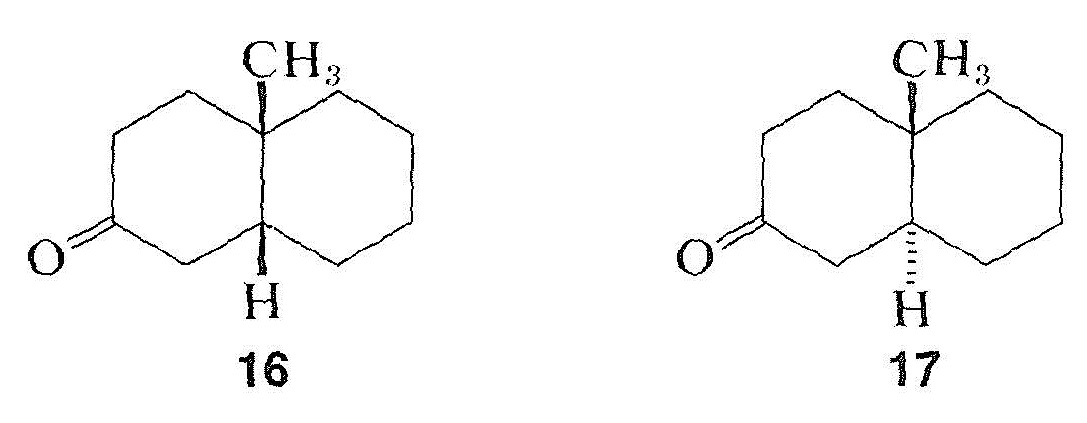
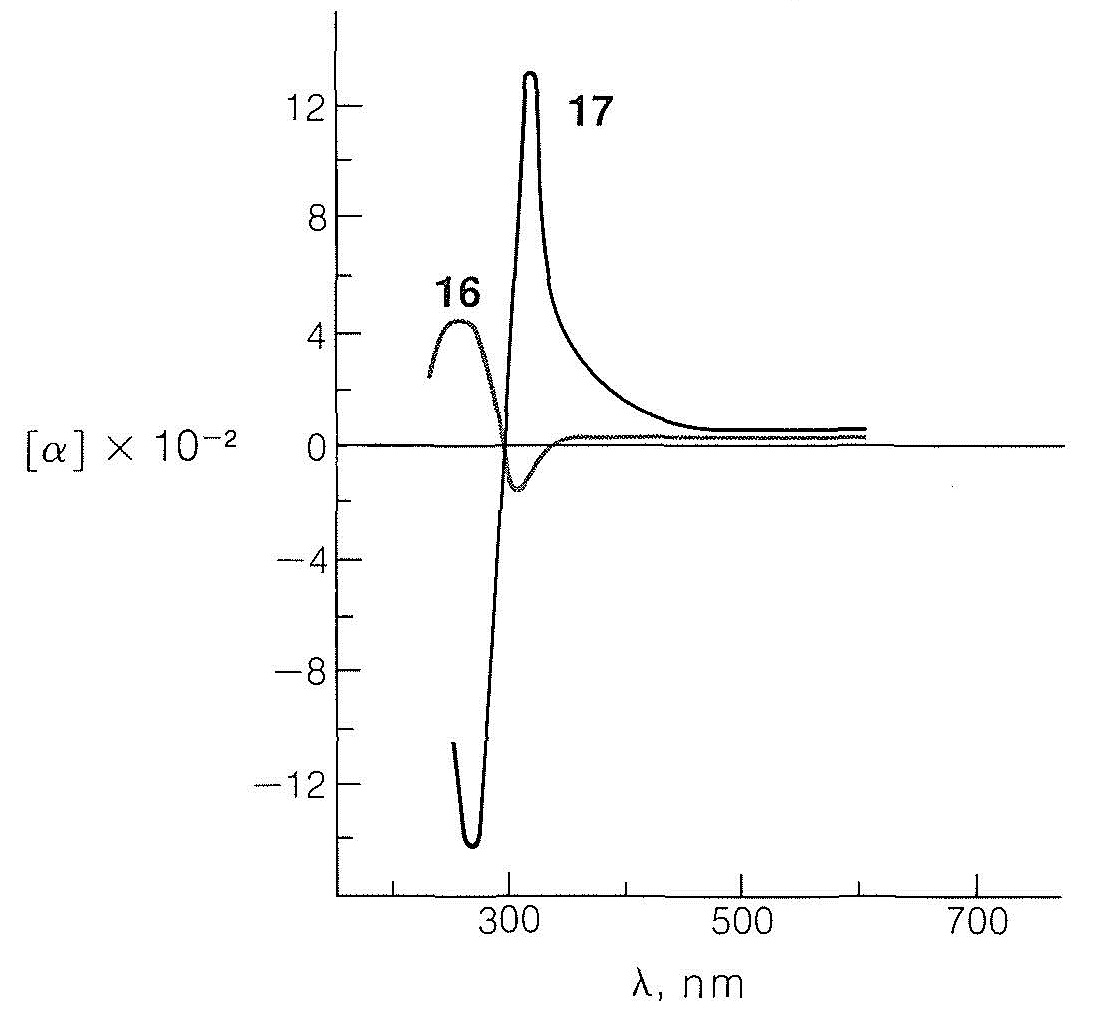
Only a small positive rotation is observed for the particular enantiomers at the wavelength of the sodium line \(\left( 589.3 \: \text{nm} \right)\) compared to the large, both positive and negative, rotations found at wavelengths between \(270 \: \text{nm}\) and \(400 \: \text{nm}\). If we measure the rotations as a function of wavelength and if, as we approach shorter wavelengths, the rotation rises to a maximum before changing sign, as it does with the trans isomer, \(17\), then the compound is said to exhibit a positive Cotton effect. The opposite behavior, as with the cis isomer, \(16\), is called a negative Cotton effect. The wavelength at the center point for the very rapid change in rotation for \(17\) is \(300 \: \text{nm}\) and corresponds to the \(n \rightarrow \pi^*\) absorption maximum of the carbonyl group in the ultraviolet absorption curve of the same compound. Thus excitation of the carbonyl group by absorption of ultraviolet light and strong rotatory dispersion of polarized light are associated phenomena. In fact, when a substance exhibits a Cotton effect, not only does it transmit clockwise and counterclockwise circularly polarized light with unequal velocities (Section 19-1), it also absorbs the two forms of light unequally.
This means that the molar extinction coefficients of the two enantiomers (\(\epsilon_l\) and \(\epsilon_r\)) are unequal in circularly polarized light. These differences in absorption (\(\epsilon_l\) and \(\epsilon_r\)) can be measured as a function of wavelength, and the curves obtained are called circular dichroism curves. They have positive or negative signs (Cotton effect) just as for optical rotatory dispersion curves.
Most of the research on optical rotatory dispersion to date has been with optically active ketones because the carbonyl chromophore conveniently has a weak absorption band in the \(300 \: \text{nm}\) region. Compounds with chromophores that absorb light strongly in the ultraviolet usually are unsatisfactory for rotatory dispersion measurements because insufficient incident light is transmitted to permit measurement of optical rotation. Weak absorption bands below about \(210 \: \text{nm}\) have not been exploited because of experimental difficulties in making the necessary measurements.
Many rotatory dispersion curves have been obtained for optically active ketones derived from steroids and triterpenes, which are monocyclic, bicyclic, and open-chain compounds. Enough data have been accumulated so that the various shapes and magnitudes of the curves are recognized as characteristic of particular structural features. A good illustration is provided by the rotatory dispersion curves for the cis- and trans-8-methylhydrindan-5-ones, \(18\) and \(19\), which are shown in Figure 19-8:
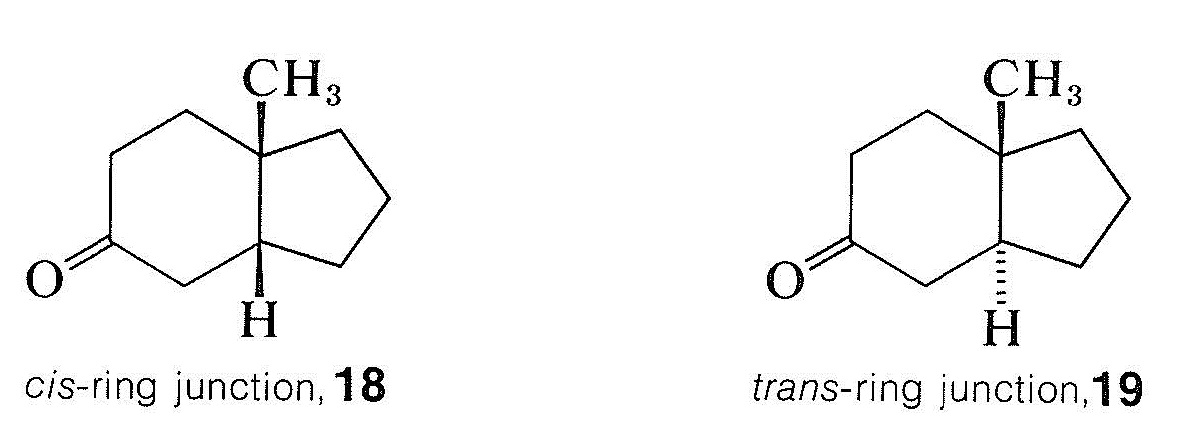
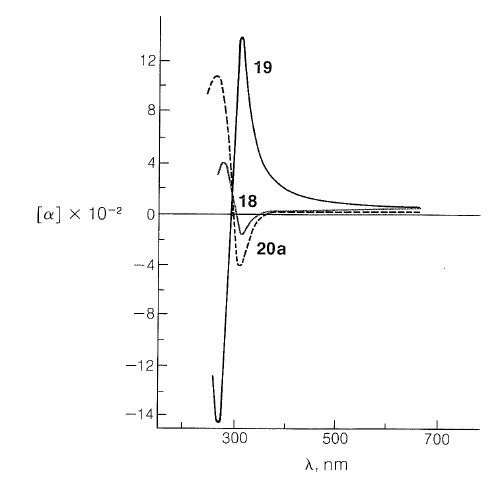
The remarkable differences in these curves are due to changes in the environment of the carbonyl groups arising from the different configurations of the hydrogens at the ring junctions. Because the rotatory dispersion curve of the closely related structure \(20a\) is very similar to that of the cis-hydrindanone, \(18\), the rings labeled \(A\) and \(B\) in \(20a\) can be inferred also to be cis oriented (see Figure 19-8):
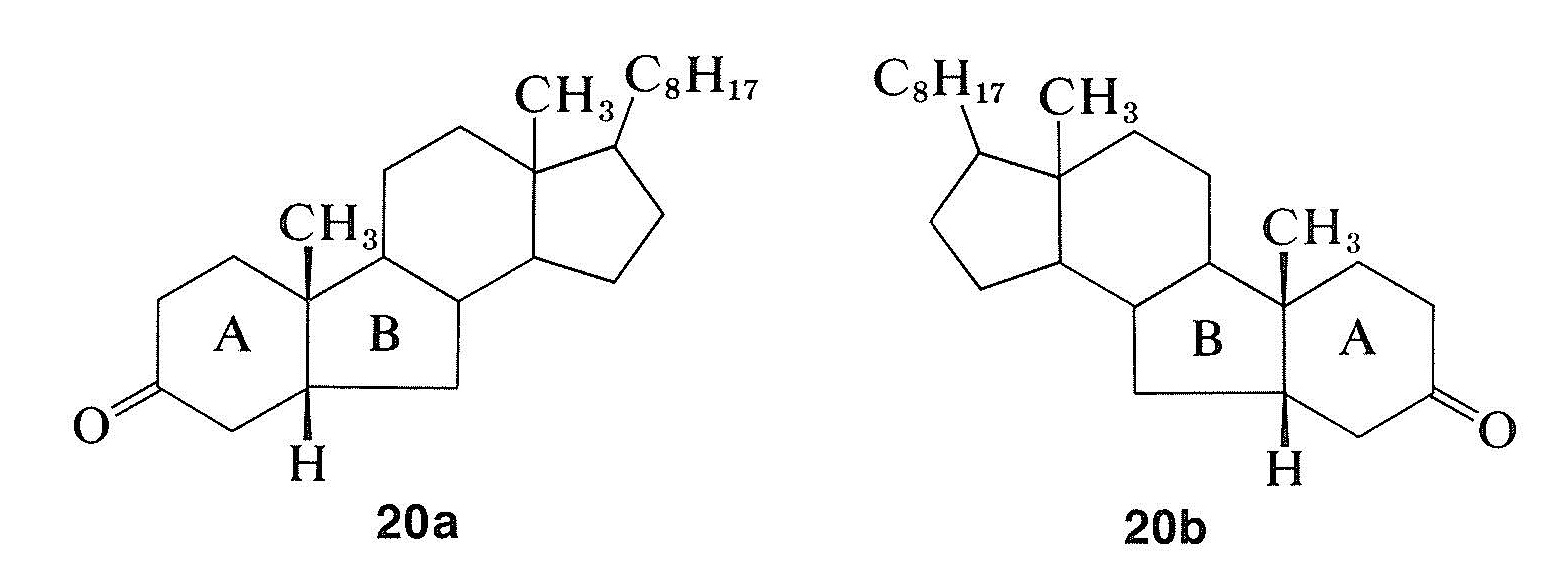
Rotatory dispersion curves often are helpful in establishing configurations; thus the relative configurations of compounds \(18\) and \(20a\) must be the same because, if they were not, the two curves would resemble mirror images of one another. Therefore, if the absolute configuration of \(18\) corresponds to the formula shown, then compound \(20a\) has the configuration shown and not \(20b\).
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


