19.1: Plane-Polarized Light and the Origin of Optical Rotation
- Page ID
- 22297
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electromagnetic radiation, as the name implies, involves the propagation of both electric and magnetic forces. At each point in an ordinary light beam, there is a component electric field and a component magnetic field, which are perpendicular to each other and oscillate in all directions perpendicular to the direction in which the beam propagates. In plane-polarized light the component electric field oscillates as in ordinary light, except that the direction of oscillation is contained within a single plane. Likewise, the component magnetic field oscillates within a plane, the planes in question being perpendicular to each other. A schematic representation of the electric part of plane-polarized light and its interaction with an optical isomer is shown in Figure 19-1. The beam of polarized light, \(XY\), has a component electric field that oscillates in the plane \(AOD\). At the point \(O\) the direction of oscillation is along \(OE\). If now at \(O\) the beam encounters a substance which has the power to cause the direction of oscillation of the electrical field to rotate through an angle \(\alpha\) to the new direction \(OE'\) in the plane \(COB\), the substance is said to be optically active.
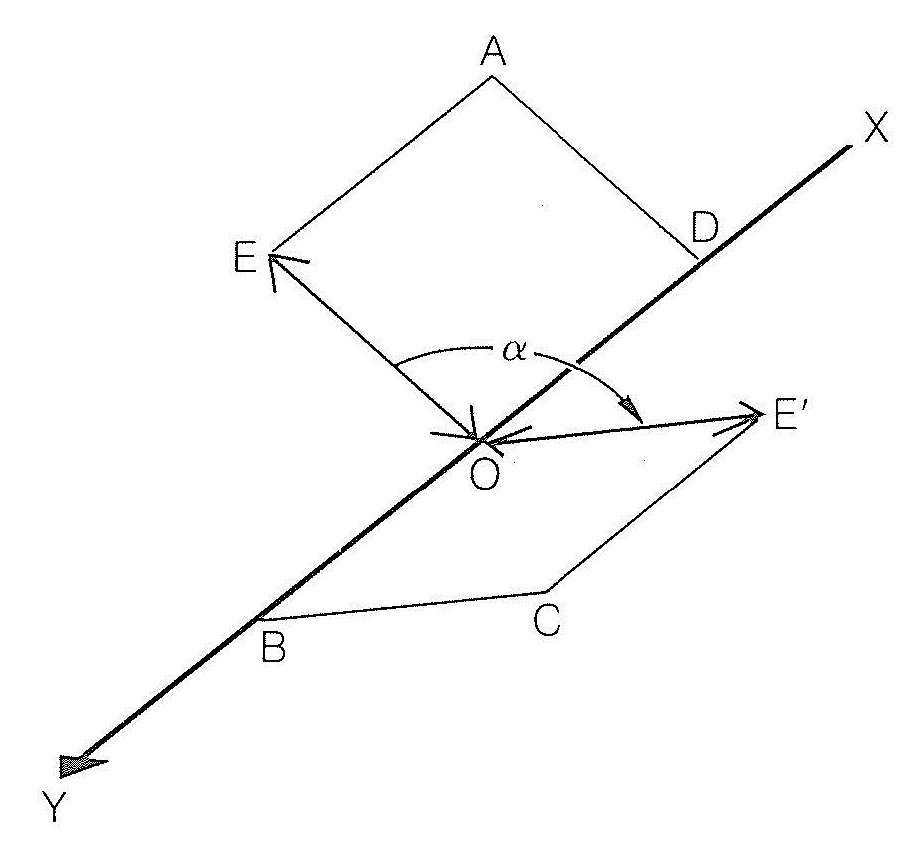
A clockwise rotation, as the observer looks towards the beam, defines the substance as dextrorotatory (i.e., rotates to the right) and the angle \(\alpha\) is taken as a positive \(\left( + \right)\) rotation. If the rotation is counterclockwise the substance is described as levorotatory (i.e., rotates to the left) and the angle \(\alpha\) is taken as a negative \(\left( - \right)\) rotation.
The question naturally arises as to why some substances interact with polarized light in this manner whereas others do not. We shall oversimplify the explanation because a rigorous treatment involves rather complex mathematics. However, it is not difficult to understand that the electric forces in a light beam impinging on a molecule will interact to some extent with the electrons within the molecule. Although radiant energy actually may not be absorbed by the molecule to promote it to higher, excited electronic-energy states (see Section 9-9A), a perturbation of the electronic configuration of the molecule can occur. One can visualize this process as a polarization of the electrons brought about by the oscillating electric field associated with the radiation.
This interaction is important to us here because it causes the electric field of the radiation to change its direction of oscillation. The effect produced by any one molecule is extremely small, but in the aggregate may be measurable as a net rotation of the plane-polarized light. Molecules such as methane, ethene and 2-propanone, which have enough symmetry so that each is identical with its reflection, do not rotate plane-polarized light. This is because the symmetry of each is such that every optical rotation in one direction is canceled by an equal rotation in the opposite direction. However, a molecule with its atoms so disposed in space that it is not symmetrical to the degree of being superimposable on its mirror image will have a net effect on the incident polarized light, because then the electromagnetic interactions do not average to zero. We characterize such substances as having chiral configurations and as being optically active.
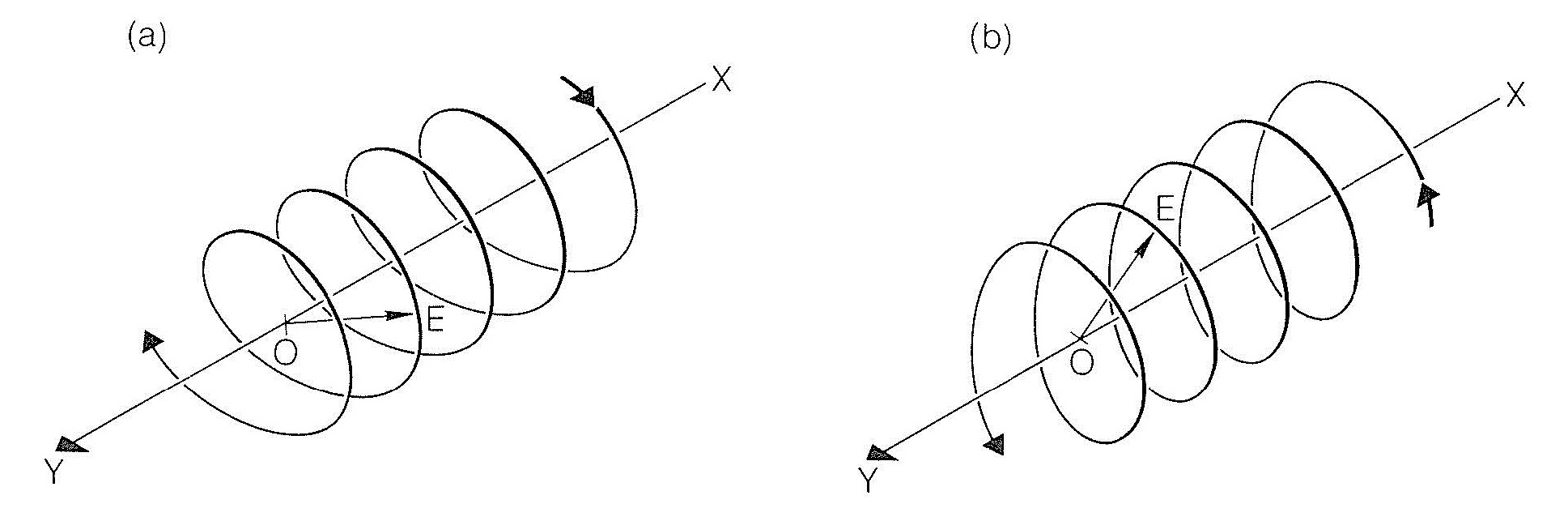
A useful model for explanation of optical rotation considers that a beam of plane-polarized light is the vector resultant of two oppositely rotating beams of circularly polarized light. This will be clearer if we understand that circularly polarized light has a component electric field that varies in direction but not in magnitude so that the field traverses a helical path in either a clockwise or counterclockwise direction, as shown in Figure 19-2.
The resultant of the two oppositely rotating electric vectors lies in a plane, and the magnitude of the resultant varies as a sine wave, shown in Figure 19-3. This amounts to plane-polarized light.
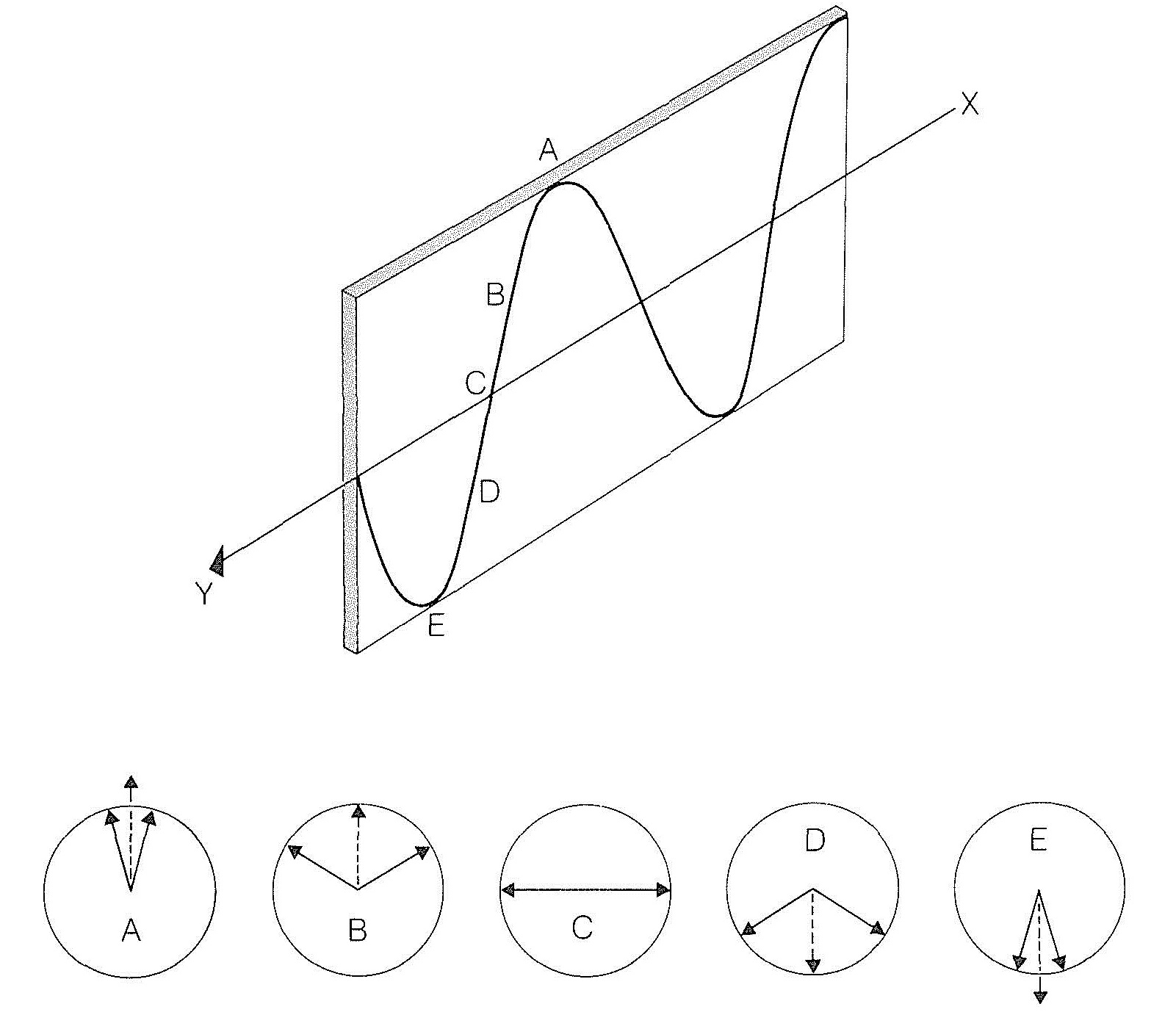
When circularly polarized light travels through an assemblage of one kind of chiral molecules, the velocity of light observed for one direction of circular polarization is different from that for the other direction of polarization. This is eminently reasonable because, no matter how a chiral molecule is oriented, the molecule presents a different aspect to circularly polarized light rotating in one direction than to that rotating in the other direction. Consequently if the electric vectors of two circularly polarized light beams initially produce a resultant that lies in a plane, and the beams then encounter a medium in which they have different velocities, one beam will move steadily ahead of the other. This will cause a continual rotation of the plane of their resultant until they again reach a medium in which they have equal velocities.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."
Template:HideTOC

