13.2: 1,3- or Conjugated Dienes. Electrophilic and Radical Addition
- Page ID
- 22074
The reactions of 1,3-butadiene are reasonably typical of conjugated dienes. The compound undergoes the usual reactions of alkenes, such as catalytic hydrogenation or radical and polar additions, but it does so more readily than most alkenes or dienes that have isolated double bonds. Furthermore, the products frequently are those of 1,2 and 1,4 addition:

Formation of both 1,2- and 1,4-addition products occurs not only with halogens, but also with other electrophiles such as the hydrogen halides. The mechanistic course of the reaction of 1,3-butadiene with hydrogen chloride is shown in Equation 13-1. The first step, as with alkenes, is formation of a carbocation. However, with 1,3-butadiene, if the proton is added to \(\ce{C_1}\) (but not \(\ce{C_2}\)), the resulting cation has a substantial delocalization energy, with the charge distributed over two carbons (review Sections 6-5 and 6-5C if this is not clear to you). Attack of \(\ce{Cl}^\ominus\) as a nucleophile at one or the other of the positive carbons yields the 1,2- or the 1,4- addition product:
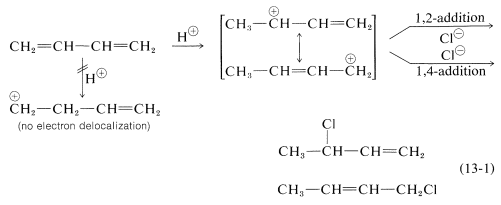
An important feature of reactions in which 1,2 and 1,4 additions occur in competition with one another is that the ratio of the products can depend on the temperature, the solvent, and also on the total time of reaction. The reason for the dependence on the reaction time is that the formation of the carbocation is reversible, and the ratio of products at equilibrium need not be the same as the ratio of the rates of attack of \(\ce{Cl}^\ominus\) at \(\ce{C_1}\) and \(\ce{C_3}\) of the carbocation. This is another example of a difference in product ratios resulting from kinetic control versus equilibrium control.
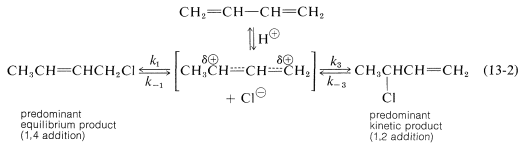
The fact is that at low temperatures the 1,2 product predominates because it is formed more rapidly, and the back reactions, corresponding to \(k_{-1}\) or \(k_{-3}\), are slow (Equation 13-2). However, at equilibrium\(^1\) the 1,4 product is favored because it is more stable, not because it is formed more rapidly.
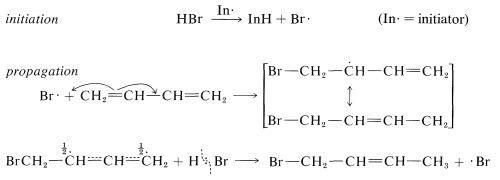
Conjugated dienes also undergo addition reactions by radical-chain mechanisms. Here, the addition product almost always is the 1,4 adduct. Thus radical addition of hydrogen bromide to 1,3-butadiene gives l-bromo-2-butene, presumably by the following mechanism:
\(^1\)The equilibrium ratio is obtained as follows. At equilibrium \(k_1/k_{-1} = \left[ \ce{CH_3CH=CHCH_2Cl} \right]/\left[ \ce{R}^\oplus \right] \left[ \ce{Cl}^\ominus \right]\) and \(k_{-3}/k_3 = \left[ \ce{R}^\oplus \right] \left[ \ce{Cl}^\ominus \right]/\left[ \ce{CH_3CHClCH=CH_2} \right]\), in which \(\ce{R}^\oplus\) is the concentration of delocalized carbocation. Multiplication of these equations gives \(k_1k_{-3}/k_{-1}k_3 = \left[ \ce{CH_3CH=CHCH_2Cl} \right]/\left[ \ce{CH_3CHClCH=CH_2} \right] = K_\text{eq}\).
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


