9.4: Why Can't We See Molecules?
- Page ID
- 22158
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
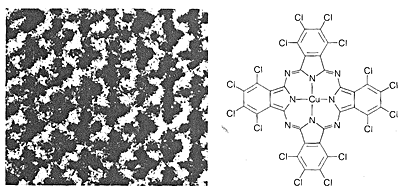
The most straightforward way to determine the structures of molecules would be to "see" how the nuclei are arranged and how the electrons are distributed. This is not possible with visible light, because the wavelengths of visible light are very much longer than the usual molecular dimensions. A beam of electrons can have the requisite short wavelengths, but small organic molecules are destroyed rapidly by irradiation with electrons of the proper wavelengths. Nonetheless, electron microscopy is a valuable technique for the study of large molecules, such as DNA, which can be stained with heavy-metal atoms before viewing, or are themselves reasonably stable to an electron beam (Figures 9-4 and 9-5).

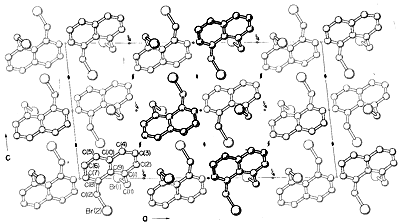
Virtually all parts of the spectrum of electromagnetic radiation, from x rays lo radio waves, have some practical application for the study of organic molecules. The use of x-ray diffraction for determination of the structures of molecules in crystals is of particular value, and in the past ten years this technique has become almost routine. Figure 9-6 shows the detailed arrangement of the carbons, hydrogens, and bromines in 1,8-bis(bromomethyl)naphthalene, \(1\), as determined by x-ray diffraction. The apparatus and techniques used are highly complex and are not available yet to very many organic laboratories.\(^3\)
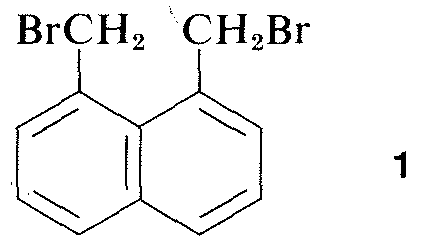
Other diffraction methods include electron diffraction, which may be used to’determine the structures of gases or of volatile liquid substances that cannot be obtained as crystals suitable for x-ray diffraction, and neutron diffraction, which has special application for crystals in which the exact location of hydrogens is desired. Hydrogen does not have sufficient scattering power for x rays to be located precisely by x-ray diffraction.
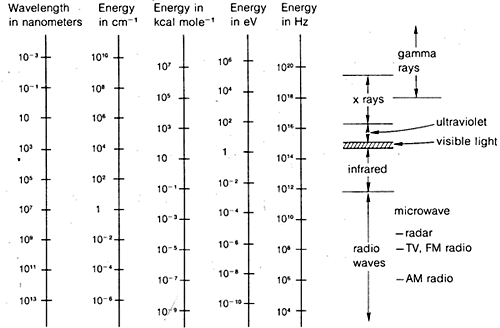
The diffraction methods can be used to determine complete structures of organic molecules, but they are not sufficiently routine to be utilized generally in practical organic laboratory work. For this reason, in the remainder of this chapter we will emphasize those forms of spectroscopy that are generally available for routine laboratory use. As will be seen, these methods are used by organic chemists in more or less empirical ways. In general, spectroscopic methods depend on some form of excitation of molecules by absorption of electromagnetic radiation and, as we have said, virtually all parts of the electromagnetic spectrum have utility in this regard. The commonly used span of the electromagnetic spectrum is shown in Figure 9-7 along with a comparison of the various units that are employed to express energy or wavelength.
The major kinds of spectroscopy used for structural analysis of organic compounds are listed in Table 9-1. The range of frequencies of the absorbed radiation are shown, as well as the effect produced by the radiation and specific kind of information that is utilized in structural analysis. After a brief account of the principles of spectroscopy, we will describe the methods that are of greatest utility to practical laboratory work. Nonetheless, it is very important to be aware of the other, less routine, methods that can be used to solve special problems, and some of these are discussed in this chapter and in Chapters 19 and 27.
You may have problems with the relationships among the variety of wavelength and frequency units commonly used in spectroscopy. The relationship between wavelength, frequency, and velocity should become clear to you by considering yourself standing on a pier watching ocean waves going by. Assuming the waves are uniformly spaced, there will be a uniform distance between the crests, which is \(\lambda\), the wavelength. The wave crests will pass by at a certain number per minute, which is \(\nu\), the frequency. The velocity, \(c\), at which the crests move by you is related to \(\lambda\) and \(\nu\) by the relationship \(c = \lambda \nu\).
This is not really very complicated and it applies equally well to water waves or electromagnetic radiation. What is almost needlessly complicated is the variety of units commonly used to express \(\lambda\) and \(\nu\) for electromagnetic radiation. One problem is tradition, the other is the desire to avoid very large or very small numbers. Thus, as Figure 9-7 shows, we may be interested in electromagnetic wavelengths that differ by as much as a factor of \(10^{16}\). Because the velocity of electromagnetic radiation in a vacuum is constant at \(3 \times 10^8 \: \text{m sec}^{-1}\), the frequencies will differ by the same factor.
Units commonly used for wavelength are meters (\(\text{m}\)), centimeters (\(\text{cm}\)), nanometers (\(\text{nm}\)), and microns (\(\mu\)). In the past, angstroms (\(Å\)) and millimicrons (\(\text{m} \mu m\)) also were used rather widely.
\[1 \: \text{m} = 10^2 \: \text{cm} = 10^9 \: \text{nm} = 10^6 \: \mu m\]
\[10^{-2} \: \text{m} = 1 \: \text{cm} = 10^7 \: \text{nm} = 10^4 \: \mu m\]
\[10^{-6} \: \text{m} = 10^{-4} \: \text{cm} = 10^3 \: \text{nm} = 1 \: \mu m\]
\[10^{-9} \: \text{m} = 10^{-7} \: \text{cm} = 1 \: \text{nm} = 10^{-3} \: \mu m= 1 \: \text{m} \mu m= 10 \: \text{Å}\]
Frequency units are in cycles per second (cps) or hertz (\(\text{Hz}\)), which are equivalent (radians per second are used widely by physicists).
Table 9-1: Principal Spectroscopic Techniques Currently in Use for Analysis of Molecular Structure

\[1 \: \text{Hz} = 10^{-6} \: \text{MHz} \cong 3.3 \times 10^{-11} \: \text{cm}^{-1}\]
\[10^6 \: \text{Hz} = 1 \: \text{MHz} \cong 3.3 \times 10^{-5} \: \text{cm}^{-1}\]
\[3 \times 10^{10} \: \text{Hz} = 3 \times 10^4 \: \text{MHz} \cong 1 \: \text{cm}^{-1}\]
\(^3\)A useful description of how molecular structures can be determined by "x-ray vision" is given in Chapter XI of Organic Molecules in Action by M. Goodman and F. Morehouse, Gordon and Breach, New York, 1973.
References
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


