20.5: Derivatives of Glucose
- Page ID
- 22304
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Determination of the Oxide Ring Size
Although we now have powerful spectroscopic methods available to determine the sizes of the oxide rings formed by the simple monosaccharides, the way in which this was done chemically for glucose highlights the difference in reactivity between ether and alcohol functions. The acid-catalyzed methylation of glucose with methanol to give two distinct glucosides, methyl \(\alpha\)-\(D\)-glucoside and methyl \(\beta\)-\(D\)-glucoside, corresponds to displacement of the hemiacetal hydroxyl by methoxyl to form an acetal (see left side of Figure 20-4).
The remaining four hydroxyl groups can be methylated in basic solution by dimethyl sulfate or by methyl iodide and silver oxide in \(\ce{N}\),\(\ce{N}\)-dimethylmethanamide, \(\ce{HCON(CH_3)_2}\), solution. Hydrolysis of either of these pentamethyl glucose derivatives with aqueous acid affects only the acetal linkage and leads to a tetramethylated glucose, \(20\), as shown in Figure 20-4.
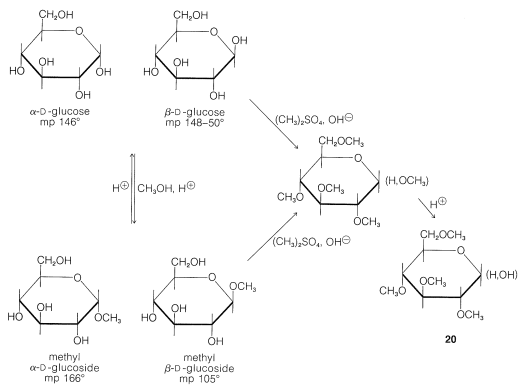
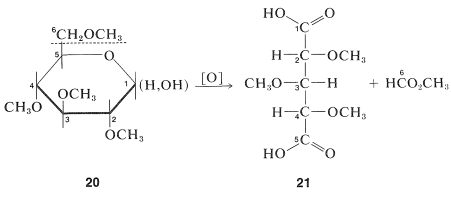
The pyranose ring structure of \(D\)-glucose originally was established by Hirst, in 1926, by converting \(D\)-glucose to a tetra-\(\ce{O}\)-methyl-\(D\)-glucose and showing that this substance actually was 2,3,4,6-tetra-\(\ce{O}\)-methyl-\(D\)-glucose, \(20\). The key feature of \(20\) is the fact that all but the two carbons involved hemiacetal formation are protected from oxidation by being substituted with \(\ce{O}\)-methyl groups in place of hydroxy groups. The largest fragment isolated from oxidation of Hirst's tetra-\(\ce{O}\)-methyl-\(D\)-glucose was a trimethoxypentanedioic acid, \(21\), and because the two carboxyl carbons must have been the ones originally involved in ring formation, the oxide ring must be between \(\ce{C_1}\) and \(\ce{C_5}\):
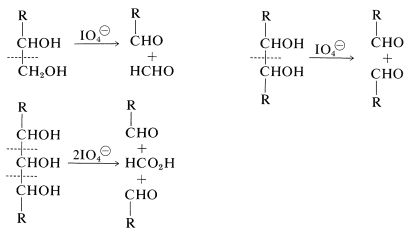
Reagents that specifically oxidize vicinal glycols [e.g., \(\ce{NaIO_4}\), \(\ce{Pb(O_2CCH_3)_4}\), and \(\ce{NaBiO_3}\); Section 16-9A] are quite helpful in determining the cyclic structures of sugars. With periodate, the numbers of moles of oxidant consumed and the moles of methanoic acid and methanal produced are different for each type of ring structure. The cleavage reactions that normally are observed follow:
Reactions with Amines and Hydrazines; Osazone Formation
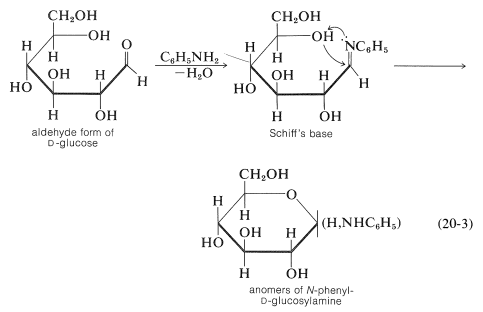
As we stated previously, glucose forms some, but not all, of the common carbonyl derivatives. The amount of free aldehyde present in solution is so small that it is not surprising that no hydrogen sulfite derivative forms. With amines, the product is not a Schiff's base but a glucosylamine of cyclic structure analogous to the hemiacetal structure of glucose, Equation 20-3. The Schiff's base is likely to be an intermediate that rapidly cyclizes to the glucosylamine:
The reaction of glucose with an excess of phenylhydrazine (phenyldiazane) is particularly noteworthy because two phenylhydrazine molecules are incorporated into one of glucose. Subsequent to the expected phenylhydrazone formation, and in a manner that is not entirely clear, the \(\ce{-CHOH}-\) group adjacent to the original aldehyde function is oxidized to a carbonyl group, which then consumes more phenylhydrazine to form a crystalline derivative called an osazone, or specifically glucose phenylosazone:
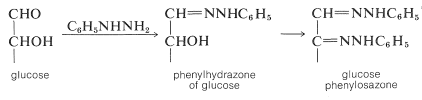
The sugar osazones usually are crystalline and are useful for characterization and identification of sugars. Fischer employed them in his work that established the configuration of the sugars. The kind of information that can be obtained is illustrated by the following example:
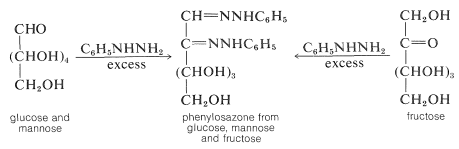
Because the same phenylosazone arises from glucose, mannose, and fructose, the configurations of \(\ce{C_3}\), \(\ce{C_4}\), and \(\ce{C_5}\) must be the same for all three sugars.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


