11.1: Oxidation-Reduction of Organic Compounds
- Page ID
- 22251
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An organic compound commonly is said to be "reduced" if reaction leads to an increase in its hydrogen content or a decrease in its oxygen content. The compound would be "oxidized" if the reverse change took place:
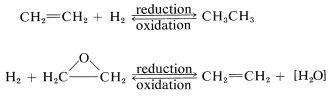
This is a very unsatisfactory definition because many oxidation-reduction or redox reactions do not involve changes in hydrogen or oxygen content, as the following example illustrates:

Redox reactions are better defined in terms of the concept of electron transfer. Thus an atom is said to be oxidized if, as the result of a reaction, it experiences a net loss of electrons; and is reduced if it experiences a net gain of electrons. This simple definition can be used to identify oxidation or reduction processes at carbon in terms of a scale of oxidation states for carbon based on the electronegativities of the atoms attached to carbon. The idea is to find out whether in a given reaction carbon becomes more, or less, electron-rich. We will use the following somewhat arbitrary rules:
- Elementary carbon is assigned the zero oxidation state.
- The oxidation state of any chemically bonded carbon may be assigned by adding \(-1\) for each more electropositive atom and \(+1\) for each more electronegative atom, and \(0\) for each carbon atom bonded directly to the carbon of interest (see Figure 10-11) for the Pauling electronegativity scale). That is,
\(-1\) for electropositive atoms, \(\ce{H}\), \(\ce{B}\), \(\ce{Na}\), \(\ce{Li}\), \(\ce{Mg}\),
\(+1\) for electronegative atoms, halogens \(\ce{O}\), \(\ce{N}\), \(\ce{S}\), and
\(0\) for carbon.
The rationale for this mode of operation can be seen if we look more closely at the example of \(\ce{CH_3Cl} + \ce{Mg} \rightarrow \ce{CH_3-Mg-Cl}\). Chlorine is more electronegative than either carbon or magnesium. Carbon is more electronegative than magnesium. Thus \(\ce{CH_3Cl}\) is written properly with a polar bond as \(\overset{\delta \oplus}{\ce{CH_3}} --- \overset{\delta \ominus}{\ce{Cl}}\), whereas the \(\ce{C-Mg}\) bond is oppositely polarized, \(\overset{\delta \ominus}{\ce{CH_3}} --- \overset{\delta \oplus}{\ce{Mg}}\). If all of the bonds were ionized completely, we could write
\[\ce{CH_3^+} + \ce{Cl}^\ominus + \ce{Mg}^0 \rightarrow \ce{CH_3} :^\ominus + \ce{Mg}^{2 \oplus} + \ce{Cl}^\ominus\]
and it would be completely clear that carbon gains two electrons (is reduced), while magnesium loses two electrons (is oxidized). But because covalent, or at most polar, bonds actually are involved, it is much more difficult to determine whether oxidation or reduction occurs. - In compounds with multiple bonds (
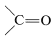 ,
, 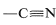 ), the attached heteroatom is counted twice or three times, depending on whether the bond is double or triple.
), the attached heteroatom is counted twice or three times, depending on whether the bond is double or triple. - A formal positive charge on carbon changes the oxidation state by \(+1\), and a formal negative charge by \(-1\); an odd electron on carbon leaves the oxidation state unchanged.
To illustrate, the oxidation state of carbon in four representative examples is determined as follows:
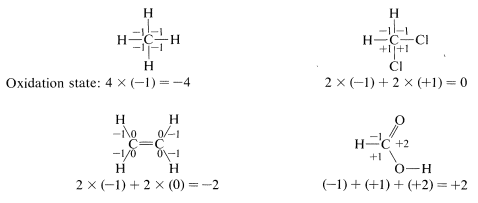
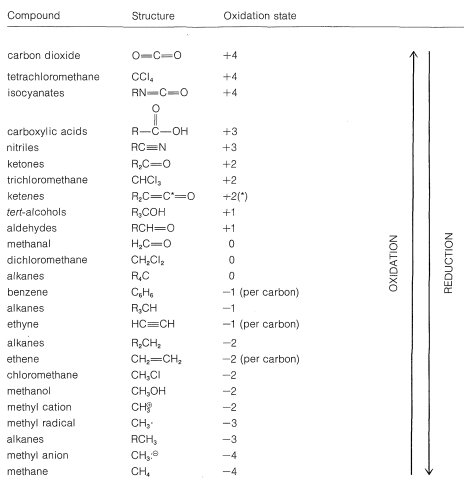
Using this approach, we can construct a carbon oxidation scale, as in Table 11-1. Any reaction that increases the degree of oxidation of carbon corresponds to a loss of electrons (oxidation), and a reaction that decreases the oxidation level corresponds to a gain of electrons (reduction). Two examples follow:
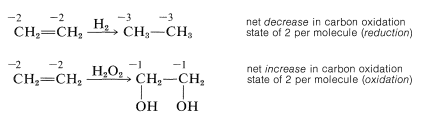
Table 11-1: Carbon Oxidation States of Representative Organic Compounds (\(\ce{R} =\) alkyl)
We recommend this scheme of oxidation states only as an aid to identify and balance redox reactions. Also, the terminology "redox" should not be confused with the mechanism of a reaction, as there is no connection between them. A moment's reflection also will show that virtually all reactions theoretically can be regarded as redox reactions, because in almost every reaction the reacting atoms experience some change in their electronic environments. Traditionally, however, reactions are described as redox reactions of carbon only when there is a net change in the oxidation state of the carbon atoms involved. An indication of just how arbitrary this is can be seen by the example of addition of water to ethene. This reaction usually is not regarded as an oxidation-reduction reaction because there is no net change in the oxidation state of the ethene carbons, despite the fact that, by our rules, one carbon is oxidized and the other reduced:
\[\overset{-2}{\ce{CH_2}} = \overset{-2}{\ce{CH_2}} + \ce{H_2O} \rightarrow \overset{-3}{\ce{CH_3}} \overset{-1}{\ce{CH_2}} \ce{OH}\]
Apart from indicating when oxidation or reduction occurs, the oxidation scales is useful in balancing redox equations. For example, consider the following oxidation of ethenylbenzene (styrene) with potassium permanganate:
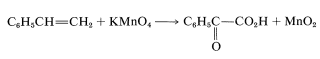
To determine how many moles of permanganate ion are required to oxidize one mole of styrene in this reaction, first determine the net change in oxidation state of the reacting carbons:

Second, determine the net change in oxidation state of manganese for \(\ce{MnO_4^-} \rightarrow \ce{MnO_2}\):
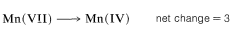
Therefore we need three moles of styrene for every eight moles of permanganate:
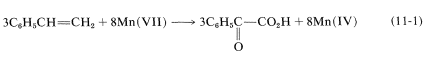
To get the overall atom and electrical balance for Equation 11-1, the requisite amounts of \(\ce{H_2O}\) must be added, but the 3:8 ratio will remain unchanged:
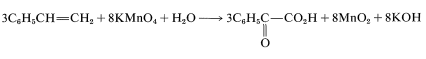
Because \(\ce{KOH}\) reacts in a nonoxidative way with carboxylic acids to form carboxylate salts \(\left( \ce{RCO_2H} + \ce{KOH} \rightarrow \ce{RCO_2K} + \ce{H_2O} \right), the final equation is

Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


