1.8: Measurement and Significant Figures
- Page ID
- 86583
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify the number of significant figures in a reported value.
- Apply the concept of significant figures to report a measurement with the proper number of digits.
Scientists have established certain conventions for communicating the degree of precision of a measurement, which is dependent on the measuring device used (See Figure \(\PageIndex{1}\)). Imagine, for example, that you are using a meterstick to measure the width of a table. The centimeters (cm) marked on the meterstick, tell you how many centimeters wide the table is. Many metersticks also have markings for millimeters (mm), so we can measure the table to the nearest millimeter. The measurement made using millimeters is more precise, it is closer to the actual length of the table. Most metersticks do not have any smaller (or more precise) markings indicated, so you cannot report the measured width of the table any more precise than to the nearest millimeter.
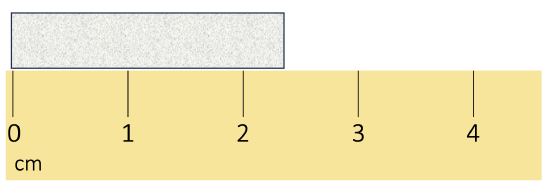
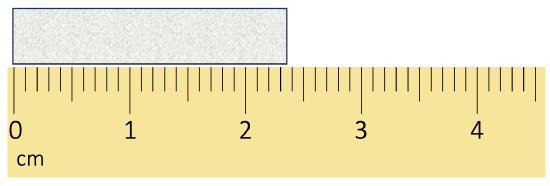
The concept of significant figures takes the limitation of measuring devices into account. The significant figures of a measured quantity are defined as all the digits known with certainty (those indicated by the markings on the measuring device) and the first uncertain, or estimated, digit (one digit past the smallest marking on the measuring device). It makes no sense to estimate and report any digits after the first uncertain one, so it is the last significant digit reported in a measurement. Zeros are used when needed to place the significant figures in their correct positions. Thus, zeros are sometimes counted as significant figures but are sometimes only used as placeholders (see the rules for significant figures below for more details).
“Sig figs” is a common abbreviation for significant figures.
Rules for Determination of Significant Figures
Consider the earlier example of measuring the width of a table with a meterstick. If the table is measured and reported as being 1,357 mm wide, the number 1,357 has four significant figures. The 1 (thousands place), the 3 (hundreds place), and the 5 (tens place) are certain; the 7 (ones place) is assumed to have been estimated. It would make no sense to report such a measurement as 1,357.0 (five Sig Figs) or 1,357.00 (six Sig Figs) because that would suggest the measuring device was able to determine the width to the nearest tenth or hundredth of a millimeter, when in fact it shows only tens of millimeters and therefore the ones place was estimated.
On the other hand, if a measurement is reported as 150 mm, the 1 (hundreds) and the 5 (tens) are known to be significant, but how do we know whether the zero is or is not significant? The measuring device could have had marks indicating every 100 mm or marks indicating every 10 mm. How can you determine if the zero is significant (the estimated digit), or if the 5 is significant and the zero a value placeholder?
The rules for deciding which digits in a measurement are significant are as follows:
Rule 1: All nonzero digits in a measurement are significant.
- 237 has three significant figures.
- 1.897 has four significant figures.
Rule 2: Zeros that appear between other nonzero digits (i.e., "middle zeros") are always significant.
- 39,004 has five significant figures.
- 5.02 has three significant figures.
Rule 3: Zeros that appear in front of all of the nonzero digits are called leading zeros. Leading zeros are never significant.
- 0.008 has one significant figure.
- 0.000416 has three significant figures.
Rule 4: Zeros that appear after all nonzero digits are called trailing zeros. A number with trailing zeros that lacks a decimal point may or may not be significant.
- 1400 is ambiguous.
- \(1.4 \times 10^3\) has two significant figures.
- \(1.40 \times 10^3\) three significant figures.
- \(1.400 \times 10^3\) has four significant figures.
Rule 5: Trailing zeros in a number with a decimal point are significant. This is true whether the zeros occur before or after the decimal point.
- 620.0 has four significant figures.
- 19.000 has five significant figures.
It needs to be emphasized that just because a certain digit is not significant does not mean that it is not important or that it can be left out. Though the zero in a measurement of 140 may not be significant, the value cannot simply be reported as 14. An insignificant zero functions as a placeholder for the decimal point. When numbers are written in scientific notation, this becomes more apparent. The measurement 140 can be written as \(1.4 \times 10^2\), with two significant figures in the coefficient or as \(1.40 \times 10^3\), with three significant figures. A number less than one, such as 0.000416, can be written in scientific notation as \(4.16 \times 10^{-4}\), which has 3 significant figures. In some cases, scientific notation is the only way to correctly indicate the correct number of significant figures. In order to report a value of 15,000,00 with four significant figures, it would need to be written as \(1.500 \times 10^7\).
Exact Quantities
When numbers are known exactly, the significant figure rules do not apply. This occurs when objects are counted rather than measured. For example, a carton of eggs has 12 eggs. The actual value cannot be 11.8 eggs, since we count eggs in whole number quantities. So the 12 is an exact quantity. Exact quantities are considered to have an infinite number of significant figures; the importance of this concept will be seen later when we begin looking at how significant figures are dealt with during calculations. Numbers in many conversion factors, especially for simple unit conversions, are also exact quantities and have infinite significant figures. There are exactly 100 centimeters in 1 meter and exactly 60 seconds in 1 minute. Those values are definitions and are not the result of a measurement.
Give the number of significant figures in each. Identify the rule for each.
- 5.87
- 0.031
- 52.90
- 00.2001
- 500
- 6 atoms
Solution
| Explanation | Answer |
|---|---|
| a. All three numbers are significant (rule 1). | 5.87 , three significant figures |
| b. The leading zeros are not significant (rule 3). The 3 and the 1 are significant (rule 1) | 0.031, two significant figures |
| c. The 5, the 2 and the 9 are significant (rule 1). The trailing zero is also significant (rule 5). | 52.90, four significant figures |
| d. The leading zeros are not significant (rule 3). The 2 and the 1 are significant (rule 1) and the middle zeros are also significant (rule 2). | 00.2001, four significant figures |
| e. The number is ambiguous. It could have one, two or three significant figures. | 500, ambiguous |
| f. The 6 is a counting number. A counting number is an exact number. | 6, infinite |
Give the number of significant figures in each.
- 36.7 m
- 0.006606 s
- 2,002 kg
- 306,490,000 people
- 3,800 g
- Answer a:
- three significant figures.
- Answer b:
- four significant figures.
- Answer c:
- four significant figures.
- Answer d:
- Infinite (Exact number)
- Answer e:
- Ambiguous, could be two, three or four significant figure.
Summary
Uncertainty exists in all measurements. The degree of uncertainty is affected in part by the quality of the measuring tool. Significant figures give an indication of the certainty of a measurement. Rules allow decisions to be made about how many digits to use in any given situation.

