14.11: Real and Ideal Gases
- Page ID
- 53831
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The behavior of a molecule depends a lot on its structure. Two compounds with the same number of atoms can act very differently. Ethanol \(\left( \ce{C_2H_5OH} \right)\) is a clear liquid that has a boiling point of about \(79^\text{o} \text{C}\). Dimethylether \(\left( \ce{CH_3OCH_3} \right)\) has the same number of carbons, hydrogens, and oxygens, but boils at a much lower temperature \(\left( -25^\text{o} \text{C} \right)\). The difference lies in the amount of intermolecular interaction (strong \(\ce{H}\)-bonds for ethanol, weak van der Waals force for the ether).
Real and Ideal Gases
An ideal gas is one that follows the gas laws at all conditions of temperature and pressure. To do so, the gas needs to completely abide by the kinetic-molecular theory. The gas particles need to occupy zero volume and they need to exhibit no attractive forces whatsoever toward each other. Since neither of those conditions can be true, there is no such thing as an ideal gas. A real gas is a gas that does not behave according to the assumptions of the kinetic-molecular theory. Fortunately, at the conditions of temperature and pressure that are normally encountered in a laboratory, real gases tend to behave very much like ideal gases.
Under what conditions then, do gases behave least ideally? When a gas is put under high pressure, its molecules are forced closer together as the empty space between the particles is diminished. A decrease in the empty space means that the assumption that the volume of the particles themselves is negligible is less valid. When a gas is cooled, the decrease in kinetic energy of the particles causes them to slow down. If the particles are moving at slower speeds, the attractive forces between them are more prominent. Another way to view it is that continued cooling of the gas will eventually turn it into a liquid and a liquid is certainly not an ideal gas anymore (see liquid nitrogen in the figure below). In summary, a real gas deviates most from an ideal gas at low temperatures and high pressures. Gases are most ideal at high temperature and low pressure.

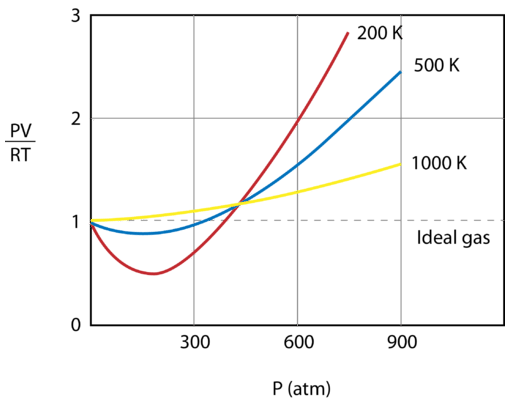
The figure below shows a graph of \(\frac{PV}{RT}\) plotted against pressure for \(1 \: \text{mol}\) of a gas at three different temperatures—\(200 \: \text{K}\), \(500 \: \text{K}\), and 1000 \: \text{K}\). An ideal gas would have a value of 1 for that ratio at all temperatures and pressures, and the graph would simply be a horizontal line. As can be seen, deviations from an ideal gas occur. As the pressure begins to rise, the attractive forces cause the volume of the gas to be less than expected and the value of \(\frac{PV}{RT}\) drops under 1. Continued pressure increase results in the volume of the particles to become significant and the value of \(\frac{PV}{RT}\) rises to greater than 1. Notice that the magnitude of the deviations from ideality is greatest for the gas at \(200 \: \text{K}\) and least for the gas at \(1000 \: \text{K}\).
The ideality of a gas also depends on the strength and type of intermolecular attractive forces that exist between the particles. Gases whose attractive forces are weak are more ideal than those with strong attractive forces. At the same temperature and pressure, neon is more ideal than water vapor because neon's atoms are only attracted by weak dispersion forces, while water vapor's molecules are attracted by relatively strong hydrogen bonds. Helium is a more ideal gas than neon because its smaller number of electrons means that helium's dispersion forces are even weaker than those of neon.
Summary
- A real gas is a gas that does not behave according to the assumptions of the kinetic-molecular theory.
- The properties of real gases and their deviations from ideality are described.

