10.12: Determining Empirical Formulas
- Page ID
- 53776
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
What is occuring in this picture?
In the early days of chemistry, there were few tools available for the detailed study of compounds. Much of the information regarding the composition of compounds came from the elemental analysis of inorganic materials. The "new" field of organic chemistry (the study of carbon compounds) faced the challenge of not being able to characterize a compound completely. The relative amounts of elements could be determined, but many of these materials had carbon, hydrogen, oxygen, and possibly nitrogen in simple ratios. Chemists had no way to determine the exact amounts of these atoms that were contained in specific molecules.
Determining Empirical Formulas
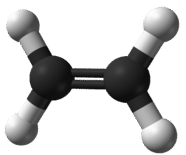
An empirical formula is one that shows the lowest whole-number ratio of the elements in a compound. Because the structure of ionic compounds is an extended three-dimensional network of positive and negative ions, all formulas of ionic compounds are empirical. However, we can also consider the empirical formula of a molecular compound. Ethene is a small hydrocarbon compound with the formula \(\ce{C_2H_4}\) (see figure below). While \(\ce{C_2H_4}\) is its molecular formula and represents its true molecular structure, it has an empirical formula of \(\ce{CH_2}\). The simplest ratio of carbon to hydrogen in ethene is 1:2. There are two ways to view that ratio. Considering one molecule of ethene, the ratio is 1 carbon atom for every 2 atoms of hydrogen. Considering one mole of ethene, the ratio is 1 mole of carbon for every 2 moles of hydrogen. So, the subscripts in a formula represent the mole ratio of the elements in that formula.
In a procedure called elemental analysis, an unknown compound can be analyzed in the laboratory in order to determine the percentages of each element contained within it. These percentages can be transformed into the mole ratio of the elements, which leads to the empirical formula. The steps to be taken are outlined below.
- Assume a \(100 \: \text{g}\) sample of the compound, so that the given percentages can be directly converted into grams.
- Use each element's molar mass to convert the grams of each element to moles.
- In order to find a whole-number ratio, divide the moles of each element by whichever of the moles from step 2 is the smallest.
- If all the moles at this point are whole numbers (or very close), the empirical formula can be written with the moles as the subscript of each element.
- In some cases, one or more of the moles calculated in step 3 will not be whole numbers. Multiply each of the moles by the smallest whole number that will convert each into a whole number. Write the empirical formula.
Example \(\PageIndex{1}\): Determining the Empirical Formula of a Compound
A compound of iron and oxygen is analyzed and found to contain \(69.94\%\) iron and \(30.06\%\) oxygen. Find the empirical formula of the compound.
Solution
Step 1: List the known quantities and plan the problem.
Known
- \(\%\) of \(\ce{Fe} = 69.94\%\)
- \(\%\) of \(\ce{O} = 30.06\%\)
Unknown
- Empirial formula = Fe?O?
Steps to follow are outlined in the text.
Step 2: Calculate.
1. Assume a \(100 \: \text{g}\) sample.
\[69.94 \: \text{g} \: \ce{Fe}\nonumber \]
\[30.06 \: \text{g} \: \ce{O}\nonumber \]
2. Convert to moles.
\[69.94 \: \text{g} \: \ce{Fe} \times \frac{1 \: \text{mol} \: \ce{Fe}}{55.85 \: \text{g} \: \ce{Fe}} = 1.252 \: \text{mol} \: \ce{Fe}\nonumber \]
\[30.06 \: \text{g} \: \ce{O} \times \frac{1 \: \text{mol} \: \ce{O}}{16.00 \: \text{g} \: \ce{O}} = 1.879 \: \text{mol} \: \ce{O}\nonumber \]
3. Divide both moles by the smallest of the results.
\[\frac{1.252 \: \text{mol} \: \ce{Fe}}{1.252} = 1 \: \text{mol} \: \ce{Fe} \: \: \: \: \: \frac{1.879 \: \text{mol} \: \ce{O}}{1.252} = 1.501 \: \text{mol} \ce{O}\nonumber \]
4/5. Since the moles of \(\ce{O}\) is still not a whole number, both moles can be multiplied by 2, while rounding to a whole number.
\[1 \: \text{mol} \: \ce{Fe} \times 2 = 2 \: \text{mol} \: \ce{Fe} \: \: \: \: \: 1.501 \: \text{mol} \: \ce{O} \times 2 = 3 \: \text{mol} \: \ce{O}\nonumber \]
The empirical formula of the compound is \(\ce{Fe_2O_3}\).
Step 3: Think about your result.
The subscripts are whole numbers and represent the mole ratio of the elements in the compound. The compound is the ionic compound iron (III) oxide.
Summary
- A process is described for the calculation of the empirical formula for a compound based on the percent composition of that compound.
Review
- What is an empirical formula?
- What does an empirical formula tell you?
- What does it not tell you?

