Skip to main content
Chemistry LibreTexts

5.7: Spectral Lines of Atomic Hydrogen

  1. Last updated
  2. Save as PDF
  • Page ID
    52965

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

     Man fixing car engine
    Figure \(\PageIndex{1}\) (Credit: CK-12 Foundation; Source: CK-12 Foundation; License: CK-12 Curriculum Materials license)

    Can you fix a car engine?

    While less common in this day and age, there was a time when many people could work on their own cars if there was a problem. Today, engines are computerized and require specialized training and tools in order to be fixed. When people did their own repairs, it was sometimes a trial and error process. Maybe the spark plugs needed to be replaced. No, that didn’t fix the problem completely, but it was a start in the right direction. Science operates the same way. A theory that is developed may work for a while, but then there are data that the theory cannot explain. This means that it's time for a newer and more inclusive theory.

    Spectral Lines of Hydrogen

    Bohr's model explains the spectral lines of the hydrogen atomic emission spectrum. While the electron of the atom remains in the ground state, its energy is unchanged. When the atom absorbs one or more quanta of energy, the electron moves from the ground state orbit to an excited state orbit that is further away. Energy levels are designated with the variable \(n\). The ground state is \(n=1\), the first excited state is \(n=2\), and so on. The energy that is gained by the atom is equal to the difference in energy between the two energy levels. When the atom relaxes back to a lower energy state, it releases energy that is again equal to the difference in energy of the two orbits (see below).

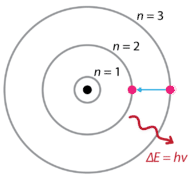
    Figure \(\PageIndex{2}\): Bohr model of the atom: electron is shown transitioning from the \(n=3\) energy level to the \(n=2\) energy level. The photon of light that is emitted has a frequency that corresponds to the difference in energy between the two levels. (Credit: Zachary Wilson; Source: CK-12 Foundation; License: CC BY-NC 3.0(opens in new window))

    The change in energy, \(\Delta E\), then translates to light of a particular frequency being emitted according to the equation \(E = h \nu\). Recall that the atomic emission spectrum of hydrogen had spectral lines consisting of four different frequencies. This is explained in the Bohr model by the realization that the electron orbits are not equally spaced. As the energy increases further and further from the nucleus, the spacing between the levels gets smaller and smaller.

    Based on the wavelengths of the spectral lines, Bohr was able to calculate the energies that the hydrogen electron would have in each of its allowed energy levels. He then mathematically showed which energy level transitions correspond to the spectral lines in the atomic emission spectrum (see below).

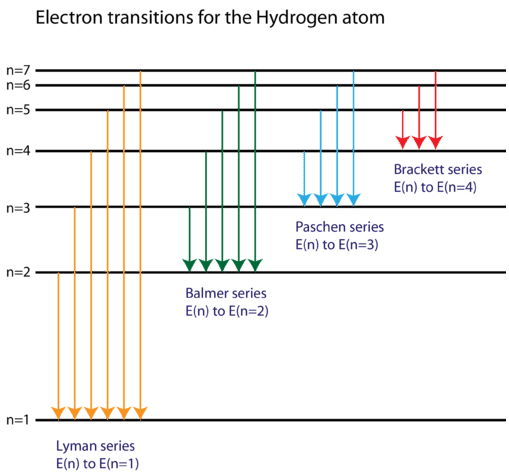
    CK12 Screenshot 5-7-2.png
    Figure \(\PageIndex{3}\): The electron energy level diagram for the hydrogen atom. (Credit: Christopher Auyeung; Source: CK-12 Foundation; License: CC BY-NC 3.0(opens in new window))

    He found that the four visible spectral lines corresponded to transitions from higher energy levels down to the second energy level \(\left( n=2 \right)\). This is called the Balmer series. Transitions ending in the ground state \(\left( n=1 \right)\) are called the Lyman series, but the energies released are so large that the spectral lines are all in the ultraviolet region of the spectrum. The transitions called the Paschen series and the Brackett series both result in spectral lines in the infrared region, because the energies are too small.

    Bohr's model was a tremendous success in explaining the spectrum of the hydrogen atom. Unfortunately, when the mathematics of the model were applied to atoms with more than one electron, it was not able to correctly predict the frequencies of the spectral lines. While Bohr's model represented a great advancement in the atomic model and the concept of electron transitions between energy levels is valid, improvements were needed in order to fully understand all atoms and their chemical behavior.

    Summary

    • Emission lines for hydrogen correspond to energy changes related to electron transitions.
    • The Bohr model works only for the hydrogen atom.

    Review

    1. What happens when a hydrogen atom absorbs one or more quanta of energy?
    2. How do we detect the change in energy?
    3. What electron transitions are presented by the lines of the Paschen series?
    4. Does the Bohr model work for atoms other than hydrogen?

    This page titled 5.7: Spectral Lines of Atomic Hydrogen is shared under a CK-12 license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

    CK-12 Foundation
    LICENSED UNDER
    CK-12 Foundation is licensed under CK-12 Curriculum Materials License