4.19: Atomic Mass Unit

Last updated
Save as PDF

Page ID: 52944

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The current system of measurement in the United States is a hodge-podge of different units, many of which are hard to interconvert. We at least have standardized units these days, unlike centuries past. At one time, measurements of length were defined as the distance from the end of one appendage to another. For example, the yard was defined as the distance from the king's nose to the tip of his thumb, when his arm was stretched out.

Standardized measurements make it possible for people everywhere to get the same amount of something. Note the red and white labels on the gas pump pictured below. These labels certify that the gas pump has been checked, and is pumping an accurate gallon of gas. Standard measurements in science are very important so that we can compare experimental data from one lab to another, and make sure that we are all talking about the same thing.

Atomic Mass

Masses of individual atoms are very, very small. Using a modern device called a mass spectrometer, it is possible to measure such miniscule masses. An atom of oxygen-16, for example, has a mass of \(2.66 \times 10^{-23} \: \text{g}\). While comparisons of masses measured in grams would have some usefulness, it is far more practical to have a system that will allow us to more easily compare relative atomic masses. Scientists decided on using the carbon-12 nuclide as the reference standard by which all other masses would be compared. By definition, one atom of carbon-12 is assigned a mass of 12 atomic mass units \(\left( \text{amu} \right)\). An atomic mass unit is defined as a mass equal to one twelfth the mass of an atom of carbon-12. The mass of any isotope of any element is expressed in relation to the carbon-12 standard. For example, one atom of helium-4 has a mass of \(4.0026 \: \text{amu}\). An atom of sulfur-32 has a mass of \(31.972 \: \text{amu}\).

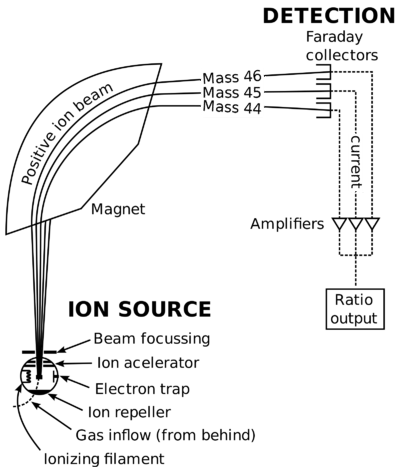
Figure \(\PageIndex{2}\): Mass spectrometer schematic. (Credit: Devon Fyson, based on image created by the U.S. Geological Survey; Source: http://commons.wikimedia.org/wiki/File:Mass_Spectrometer_Schematic.svg(opens in new window); License: Public Domain)

The carbon-12 atom has six protons and six neutrons in its nucleus for a mass number of 12. Since the nucleus accounts for nearly all of the mass of the atom, a single proton or single neutron has a mass of approximately \(1 \: \text{amu}\). However, as seen by the helium and sulfur examples, the masses of individual atoms are not whole numbers. This is because an atom's mass is affected very slightly by the interactions of the various particles within the nucleus, and the small mass of the electron is taken into account.

Summary

Carbon-12 is the reference for all atomic mass calculations.
An atomic mass unit is defined as a mass equal to one twelfth the mass of an atom of carbon-12.
The mass of an atom is affected by the interactions of particles within the nucleus.

Review

What instrument is used to measure the mass of atoms?
How much does a single oxygen-16 atom weigh in grams?
What is the reference standard for atomic mass units?
How is an atomic mass unit defined?
Why are the numbers for atomic mass of individual atoms not whole numbers?