8.2: Radioactivity

The cause of radioactivity

Only a particular combination of protons and neutrons forms stable nucleoids; the rest are unstable nucleoids, as illustrated in Fig. 8.2.1. The observations on the stable nucleoids are the following.

Observations on the stable nucleoids

1. Hydrogen with one proton and no neutrons is a stable nucleoid.
2. Other light nucleoids, up to atomic number 20 are usually stable when the number of protons is equal to the number of neutrons
3. The medium nucleoids from atomic numbers 20 to 82 are generally stable when the number of neutrons is more than the number of protons.
4. The heavier nucleoids with atomic number 84 or more are unstable.

Figure \(\PageIndex{1}\): Graph of isotopes by type of nuclear decay. Orange and blue nuclides are unstable, with the black squares between these regions representing stable nuclides. The unbroken line passing below many of the nuclides represents the theoretical position on the graph of nuclides for which the proton number is the same as the neutron number. The graph shows that elements with more than 20 protons must have more neutrons than protons, in order to be stable. Source: Table_isotopes.svg: Napy1kenobiderivative work: Sjlegg / CC BY-SA (https://creativecommons.org/licenses/by-sa/3.0)

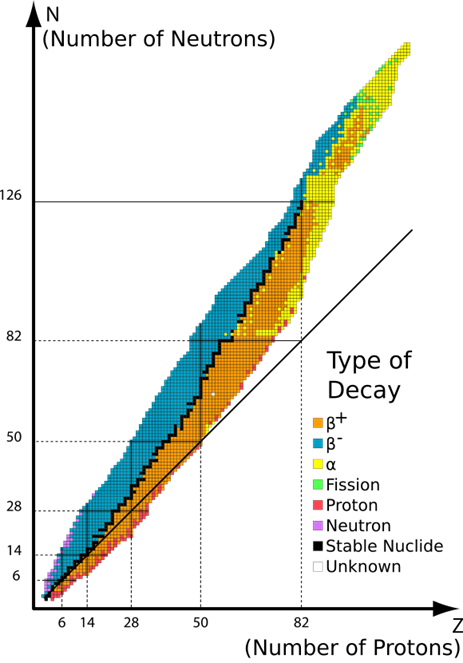
The nucleoids shown as black dots in Fig. 8.2.1 are naturally occurring stable nucleoids. All nucleoids shown in colored dots other than black are unstable.

Note

The unstable nucleoids are radioactive -they spontaneously disintegrate, i.e., they tend to re-arrange the nucleon composition in the nucleus to become a more stable nucleoid.

The radioactivity releases energy and particles, i.e., nuclear radiation along with the re-arrangement of the nucleus, as explained in the following sections.

Alpha-decay

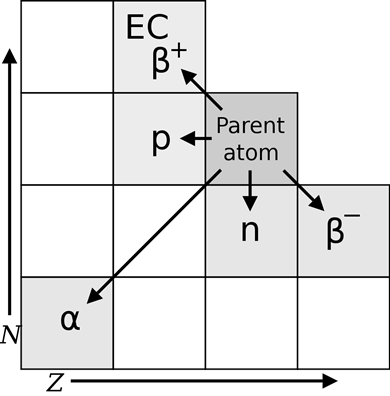
The \(\ce{\alpha}\)-emission is one of the important processes for stabilizing heavy unstable nucleoids shown with yellow dots in Fig. 8.2.1. Since the \(\ce{\alpha}\)-particle has two protons and two neutrons, the daughter nucleoid produced along with the \(\ce{\alpha}\)-decay has two fewer protons and four fewer mass numbers in it than the parent nucleoid, as illustrated in Fig. 8.2.2.

Figure \(\PageIndex{2}\): Illustration of alpha-decay process. Source: PerOX / CC0

For example:

\[\ce{_92^238U -> _90^234Th + _2^4He}\nonumber\]

Some times the \(\ce{\alpha}\)-decay is accompanied by \(\ce{\gamma}\)-emission, e.g.:

\[\ce{_84^210Po -> _82^206Pb + _2^4He + \gamma}\nonumber\]

Note that the \(\ce{\gamma}\)-rays have zero mass, so they do not change the atomic number and mass number of the parent nucleoid.

Steps of writing a nuclear reaction equation

1. Write the symbols of the know nucleoids, particles, and radiations in the reactants and products, separated by an arrow. Leave a question mark for the unknown pieces of information.
2. Balance the mass number on the two sides of the equation.
3. Balance the atomic number on the two sides of the equation.
4. Wright the symbols of the unknown nucleoid or particles by finding them in the periodic table, based on the atomic numbers.

\(\ce{\alpha}\)-decay in smoke detectors

Smoke detectors used in homes need \(\ce{\alpha}\)-particles for their function. Americium-241 is the \(\ce{\alpha}\)-decay-emitter used in the smoke detectors.

Example \(\PageIndex{1}\)

Write the nuclear reaction equation for the \(\ce{\alpha}\)-decay of americium-241.

Solution

Step 1. The symbol and the atomic number of americium in the periodic table are Am and 95, respectively. So the initial equation is:

\[\ce{_95^241Am -> _{?}^{?}{?} + _2^4He}\nonumber\]

Step 2. Balance the mass number on the two sides of the equation, i.e., the mass number of unknown nucleoid is 241-4 = 237:

\[\ce{_95^241Am -> _{?}^{237}{?} + _2^4He}\nonumber\]

Step 3. Balance the atomic number on the two sides of the equation, i.e., the atomic number of the unknown nucleoid is 95-2 = 93:

\[\ce{_95^241Am -> _{93}^{237}{?} + _2^4He}\nonumber\]

Step 4. Find the symbol of the unknown nucleoid from the periodic table of elements, i.e., the element at atomic number 93 is neptunium symbol Np:

\[\ce{_95^241Am -> _{93}^{237}{Np} + _2^4He}\nonumber\]

This is the balanced nuclear equation for the \(\ce{\alpha}\)-decay of americium-241 in smoke detectors.

Radium-226, present in many types of rocks and soils, is an \(\ce{\alpha}\)-emitter producing radon-226 in the process. The radon-226 is also an \(\ce{\alpha}\)-emitter that can diffuse into houses from the rocks and soil underneath the buildings. Radon is an environmental health issue in the buildings when its concentration becomes above a certain level. The nuclear equation for the \(\ce{\alpha}\)-decay of radon-222 is the following.

\[\ce{_86^222Rn -> _{84}^{218}{Po} + _2^4He}\nonumber\]

Example \(\PageIndex{2}\)

Write the nuclear equation for the α-decay of radium-226.

Solution

Step 1. The initial equation is:

\[\ce{_88^226Rn -> _{?}^{?}{?} + _2^4He}\nonumber\]

Step 2. Balance the mass number on the two sides of the equation, i.e., is 226-4 = 222:

\[\ce{_88^226Rn -> _{?}^{222}{?} + _2^4He}\nonumber\]

Step 3. Balance the atomic number on the two sides of the equation, i.e., 88-2 = 86:

\[\ce{_88^226Rn -> _{86?}^{222}{?} + _2^4He}\nonumber\]

Step 4. Find the symbol of the unknown nucleoid from the periodic table of elements, i.e., the element at atomic number 86 is radon symbol Rn:

\[\ce{_88^226Rn -> _{?}^{222}{Rn} + _2^4He}\nonumber\]

This is the balanced nuclear equation for the \(\ce{\alpha}\)-decay of radium-226 in rocks and soil.

Beta-decay

The nucleoids marked blue in Fig. 8.2.1. have more neutrons than needed for stability. They usually stabilize them by converting one of the neutrons (n) into a proton (p) and an electron (e) by the following nuclear process:

\[\ce{_{0}^{1}{n} -> _{1}^{1}{p} + _{-1}^{0}{e}}\nonumber\]

The proton stays in the nucleus, but the electron emits from the nucleus, as illustrated in Fig. 8.2.3. The emitted electron is called \(\ce{\beta}\)-particle. The process of the \(\ce{\beta}\)-particle emission is called beta-decay. Note that the neutron has zero atomic number as there is no proton in it, and the electron has a -1 atomic number to balance the +1 atomic number of the proton. Proton has +1 and electron has -1 charge, which is also balanced. The mass number of an electron is zero as it has negligible mass compared to the mass of a proton or a neutron. The electrical charges and the emission of another particle called neutrino are ignored in this equation.

Figure \(\PageIndex{3}\): Illustration of beta-decay. A neutron (n) is transformed into a proton (p) in the nucleus, ejecting an electron (e^-) and some energy as radiation. Source: Inductiveload/ Public domain

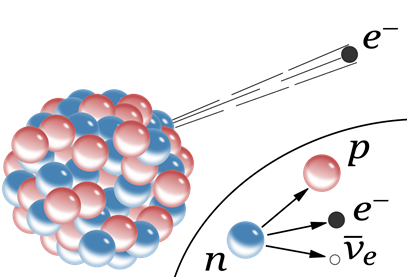
An example of β-decay is the transformation of nitrogen-16 to oxygen-17:

\[\ce{_{7}^{16}{N} -> _{8}^{16}{O} + _{-1}^{0}{e}}\nonumber\]

Note that in the \(\ce{\beta}\)-decay process, the mass number remains the same, but the atomic number increases by one in the daughter nucleus. The nuclear equation is balanced because the mass number is the same (16 = 16+0), and the atomic number is also the same (7 = 8-1) on the two sides of the equation.

Uses of some beta-emitters

Iodine-131 is used for radiation therapy of an overactive thyroid gland.

Yttrium-90 is used to treat cancer and is also injected into large joints to relieve the pain due to arthritis.

Phosphorous-32 is used to treat leukemia and other blood disorders.

Carbon-14 is used to determine the age of a fossil or an old object.

Example \(\PageIndex{3}\)

Write the nuclear equation for the \(\ce{\beta}\)-decay of iodine-131.

Solution

Step 1. The symbol and the atomic number of iodine in the periodic table are I and 53, respectively. So the initial equation is:

\[\ce{_{53}^{131}{I} -> _{?}^{?}{?} + _{-1}^{0}{e}}\nonumber\]

Step 2. Balance the mass number on the two sides of the equation, i.e., the mass number of unknown nucleoid is 131-0 = 131:

\[\ce{_{53}^{131}{I} -> _{?}^{131}{?} + _{-1}^{0}{e}}\nonumber\]

Step 3. Balance the atomic number on the two sides of the equation, i.e., the atomic number of the unknown nucleoid is 53-(-1) = 54:

\[\ce{_{53}^{131}{I} -> _{54}^{131}{?} + _{-1}^{0}{e}}\nonumber\]

Step 4. Find the symbol of the unknown nucleoid from the periodic table of elements, i.e., the element at atomic number 54 is xenon symbol Xe:

\[\ce{_{53}^{131}{I} -> _{54}^{131}{Xe} + _{-1}^{0}{e}}\nonumber\]

This is the balanced nuclear equation for the α-decay of iodine-131 that is used to treat over-active thyroid glands.

Example \(\PageIndex{4}\)

Write the nuclear equation for the β-decay of yttrium-90.

Solution

Step 1. The symbol and the atomic number of yttrium in the periodic table are Y and 39, respectively. So the initial equation is:

\[\ce{_{39}^{90}{Y} -> _{?}^{?}{?} + _{-1}^{0}{e}}\nonumber\]

Step 2. Balance the mass number on the two sides of the equation, i.e., the mass number of unknown nucleoid is 90-0 = 90:

\[\ce{_{39}^{90}{Y} -> _{?}^{90}{?} + _{-1}^{0}{e}}\nonumber\]

Step 3. Balance the atomic number on the two sides of the equation, i.e., the atomic number of the unknown nucleoid is 39-(-1) = 40:

\[\ce{_{39}^{90}{Y} -> _{40}^{90}{?} + _{-1}^{0}{e}}\nonumber\]

Step 4. Find the symbol of the unknown nucleoid from the periodic table of elements, i.e., the element at atomic number 40 is zirconium symbol Z:

\[\ce{_{39}^{90}{Y} -> _{40}^{90}{Z} + _{-1}^{0}{e}}\nonumber\]

This is the balanced nuclear equation for the β-decay of yttrium-90.

Positron emission

The nucleoids marked orange in Fig. 8.2.1. have more protons than needed for stability. They usually stabilize them by converting one of the protons (p) into a neutron (n) and a positron \(\ce{\beta^+}\) by the following nuclear process:

\[\ce{_{1}^{1}{p} -> _{0}^{1}{n} + _{1}^{0}{e}}\nonumber\]

The neutron stays in the nucleus, but the positron emits from the nucleus, as illustrated in Fig. 8.2.4. Note that the positron has a +1 mass number that balances the +1 atomic number of the proton on the other side of the equation. The positron has a +1 charge that also balances the +1 charge of the proton on the other side of the equation. The mass number of a positron is zero as it has negligible mass compared to the mass of a proton or a neutron. The electrical charges are not shown in the nuclear equation.

Figure \(\PageIndex{4}\): Illustration of positron-emission. A proton (p) is transformed into a neutron (n) in the nucleus, ejecting a positron (e⁺) and some energy as radiation. Source: Master-m1000 / Public domain

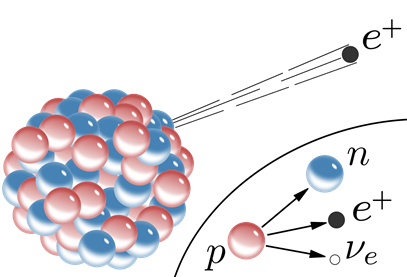
Carbon-11 is an example of positron-emitter:

\[\ce{_{6}^{11}{I} -> _{5}^{11}{B} + _{1}^{0}{e}}\nonumber\]

Note that in the positron-emission process, the mass number remains the same, but the atomic number decreases by one in the daughter nucleus. The nuclear equation is balanced because the mass number is the same (11 = 11+0), and the atomic number is also the same (7 = 5+1) on the two sides of the equation.

Uses of some positron emittors

Positron emission is used in positron emission tomography (PET) which is a medical imaging technique. Short-lived positron-emitting isotopes ¹¹C, ¹³N, ¹⁵O, and ¹⁸F used for positron emission tomography are typically produced by proton irradiation of natural or enriched targets described in a later section.

Fluorine-18 in fluorodeoxyglucose, abbreviated as [¹⁸F]FDG is a positron emitter commonly used to detect cancer, and in [¹⁸F]NaF is widely used for detecting bone formation. Other examples are oxygen-15 in [¹⁵O]H₂O used to measure blood flow and nitrogen-13 used to tag ammonia molecules for myocardial perfusion imaging.

\[\ce{_{8}^{15}{O} -> _{7}^{15}{N} + _{1}^{0}{e}}\nonumber\]

\[\ce{_{7}^{13}{N} -> _{6}^{13}{C} + _{1}^{0}{e}}\nonumber\]

Example \(\PageIndex{5}\)

Write the nuclear equation for the positron-emission of fluorine-18?

Solution

Step 1. The symbol and the atomic number of fluorine in the periodic table are F and 9, respectively. So the initial equation is:

\[\ce{_{9}^{18}{F} -> _{?}^{?}{?} + _{1}^{0}{e}}\nonumber\]

Step 2. Balance the mass number on the two sides of the equation, i.e., the mass number of unknown nucleoid is 18-0 = 131:

\[\ce{_{9}^{18}{F} -> _{?}^{131}{?} + _{1}^{0}{e}}\nonumber\]

Step 3. Balance the atomic number on the two sides of the equation, i.e., the atomic number of the unknown nucleoid is 9-(+1) = 8:

\[\ce{_{9}^{18}{F} -> _{8}^{131}{?} + _{1}^{0}{e}}\nonumber\]

Step 4. Find the symbol of the unknown nucleoid from the periodic table of elements, i.e., the element at atomic number 8 is oxygen symbol O:

\[\ce{_{9}^{18}{F} -> _{8}^{18}{?} + _{1}^{0}{e}}\nonumber\]

This is the balanced nuclear equation for the positron-emission of fluorine-18.

Gamma-emission

The gamma-rays are high-energy electromagnetic radiations that do not have mass or charge. So, pure \(\ce{\gamma}\)-emission happens from the nucleus, but it does not result in transmutation, simply the nucleoid changes from a more unstable state, called a metastable state, to a relatively stable state, as illustrated in Fig. 8.2.5.

Figure \(\PageIndex{5}\): An illustration of gamma-emission, the \(\ce{\gamma}\)-ray originates from the radioactive nucleus, changes the energy state but does not change the identity of the nucleoid. Source: Inductiveload / Public domain

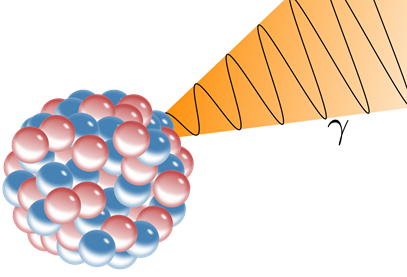
A symbol m or * next to the mass number as a superscript to the right indicates the metastable state of the parent nucleoid. For example, technetium-99m is a \(\ce{\gamma}\)-emitter widely used in medical imaging:

\[\ce{_{43}^{99m}{Tc} -> _{43}^{199}{Tc } + \gamma}\nonumber\]

Similarly, boron-11m is a \(\ce{\gamma}\)-emitter:

\[\ce{_{5}^{11m}{B} -> _{5}^{11}{B } + \gamma}\nonumber\]

Note that the nucleoid remains the same after \(\ce{\gamma}\)-emission, except for the change form metastable to a more stable state indicated by m.

Often, the \(\ce{\gamma}\)-emission accompanies \(\ce{\alpha}\)-emission or \(\ce{\beta}\)-emission. For example, polonium-210 decays by a simultaneous \(\ce{\alpha}\)-emission and \(\ce{\gamma}\)-emissions.

\[\ce{_{84}^{210}{Po} -> _{82}^{206}{Pb } + _2^4He + \gamma}\nonumber\]

Similarly, iridium-192 used in implants to treat breast cancer, and cobalt-60 used as an external radiation source for cancer treatment, simultaneously emit \(\ce{\beta}\) and \(\ce{\gamma}\)-rays.

\[\ce{_{77}^{192}{Ir} -> _{78}^{192}{Pt } + _{-1}^{0}{e} + \gamma}\nonumber\]

\[\ce{_{27}^{60}{Co} -> _{28}^{60}{Ni } + _{-1}^{0}{e} + \gamma}\nonumber\]

Iodine-131 decays to \(\ce{\beta}\)-particle and xenon-131m that is rapidly followed by a \(\ce{\gamma}\)-decay of xenon-131m.

\[\ce{_{53}^{131}{I} -> _{54}^{131m}{Xe } + _{-1}^{0}{e}}\nonumber\]

\[\ce{_{54}^{131m}{Xe} -> _{54}^{131}{Xe} + \gamma}\nonumber\]

Less common forms of radioactivity

Several relatively less common forms of radioactivity are known. Some examples are the following.

1. Neutron-emission is a mode of radioactive decay in which one or more neutrons are ejected from a nucleus.
2. Proton-emission is a rare form of radioactivity in which a proton emits from a nucleoid.
3. Spontaneous fission is a radioactive process in which a more massive nucleoid breaks into smaller nucleoids, often along with the emission of smaller nuclear particles.
4. In electron-capture, an external electron is captured to react with proton and produce a neutron in the nucleus.

For example, beryllium-7 decays by electron capture, as shown in the following equation.

\[\ce{_{4}^{7}{Be} + _{-1}^{0}{e} -> _{3}^{7}{Li} + \gamma}\nonumber\]

Note that the mass number remains the same, but the atomic number decreases by one in the electron-capture process.

Chromium-51, which is used for imaging the spleen, decays by the electron capture and \(\ce{\gamma}\)-emission.

\[\ce{_{24}^{51}{Cr} + _{-1}^{0}{e} -> _{23}^{51}{V} + \gamma}\nonumber\]

Summary of decay mode of radioactive nucleoids

Fig. 8.2.6 summarizes the changes in the nucleoid composition upon different radioactive events described above.

Figure \(\PageIndex{6}\): Transition diagram for decay modes of a radionuclide, with neutron number N and atomic number Z (shown are \(\ce{\alpha}\), , β^± are beta-particle, and positron,p⁺is proton, and n⁰ is neutron missions, EC denotes electron capture). Source: MarsRover / GFDL (http://www.gnu.org/copyleft/fdl.html)