7.6: The volume-amount relationship

Last updated
Save as PDF

Page ID: 371604

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figure \(\PageIndex{1}\) illustrates the effect of the amount of gas on the volume. Adding more gas molecules increases the collision frequency of the molecules with the walls increasing the gas pressure. The gas expands to reduce pressure until the pressure of gas in the chamber is equal to the outside pressure.

Avogadro's law

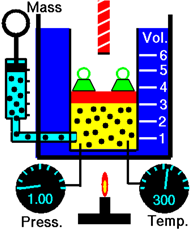
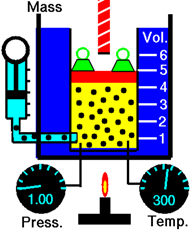
Avogadro’s law states that the volume of a gas is directly proportional to the amount of gas in moles provided the temperature and pressure of the gas are not changed.

The mathematical forms of Avogadro's law are the following.

\[V\propto {n}\nonumber\]

\[V=\mathrm{k}n\nonumber\]

\[\dfrac{V}{n}=\mathrm{k}\nonumber\]

where \(V\) is the volume, \(n\) is the number of moles, and \(k\) is the constant for the gas under the conditions of constant temperature and pressure. Since \(\mathrm{V} / \mathrm{n}\) is a constant, it implies that:

\[\dfrac{V_{1}}{n_{1}}=\dfrac{V_{2}}{n_{2}}=\mathrm{k}\nonumber\]

where \(V_{1}\) and \(n_{1}\) is initial volume and the initial amount of gas, respectively, and \(V_{2}\) and \(n_{2}\) is final volume and the final amount of gas in mole, provided the temperature and pressure are not changed.

Example \(\PageIndex{1}\)

A weather balloon containing \(3.0\) moles of helium has a volume of \(66 \mathrm{~L}\). What is the final volume if \(2.0\) moles of helium is added to it. The pressure and temperature of the gas do not change?

Solution

Given \(\quad V_{1}=66 L, \quad n_{1}=3.0 \mathrm{~mol}, \quad V_{2}=?, \quad n_{2}=3.0+2.0=5.0 \mathrm{~mol}\)

Formula:

\[\dfrac{V_{1}}{n_{1}}=\dfrac{V_{2}}{n_{2}}, \nonumber\]

rearrange the formula to isolate the desired variable:

\[V_{2}=\dfrac{V_{1} n_{2}}{n_{1}}. \nonumber\]

Plug in the values and calculate:

\[V_{2}=\dfrac{66 \mathrm{~L} \times \times 5.0 \mathrm{~mol}}{3.0 \mathrm{~mol}}=110 \mathrm{~L}. \nonumber\]