8.11: Partial Pressure and Dalton's Law
- Page ID
- 444191
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define Dalton's law of partial pressures.
- Use Dalton's law to calculate partial pressure of a gas in a mixture.
One of the properties of gases is that they mix with each other. When they do so, they become a solution—a homogeneous mixture. Some of the properties of gas mixtures are easy to determine if we know the composition of the gases in the mix.
In gas mixtures, each component in the gas phase can be treated separately because, according to the kinetic theory of gases, there are little to no attractive or repulsive forces between particles. Each component of a gas mixture shares the same temperature and volume, (remember that gases expand to fill the volume of their container; gases in a mixture continue to do that as well). However, each individual gas will have its own pressure within a mixture. This is called the partial pressure of a gas, \(P_i\). Partial pressures are expressed in torr, millimeters of mercury, or atmospheres like any other gas pressure; however, we use the term pressure when talking about pure gases and the term partial pressure when we are talking about the individual gas components in a mixture.
Dalton's law of partial pressures states that the total pressure of a gas mixture, \(P_{tot}\), is equal to the sum of the partial pressures of the components, \(P_i\):
which is expressed algebraically as
\[P_{total}=P_1+P_2+P_3 ... = \sum_i P_i \nonumber \]
or, equivalently
\[ P_{total} = \dfrac{RT}{V} \sum_i n_i \nonumber \]
where \(i\) counts over all gases in mixture.
Although this law may seem trivial, it reinforces the idea that gases behave independently of each other.
A mixture of H2 at 2.33 atm and N2 at 0.77 atm is in a container. What is the total pressure in the container?
Solution
Dalton's law of partial pressures states that the total pressure is equal to the sum of the partial pressures. We simply add the two pressures together:
Ptot = 2.33 atm + 0.77 atm = 3.10 atm
N2 and O2. In 760 torr of air, the partial pressure of N2 is 608 torr. What is the partial pressure of O2?
- Answer
-
152 torr
A 2.00 L container with 2.50 atm of H2 is connected to a 5.00 L container with 1.90 atm of O2 inside. The containers are opened, and the gases mix. What is the final pressure inside the containers?
Solution
Because gases act independently of each other, we can determine the resulting final pressures using Boyle's law and then add the two resulting pressures together to get the final pressure. The total final volume is 2.00 L + 5.00 L = 7.00 L. First, we use Boyle's law to determine the final pressure of H2:
(2.50 atm)(2.00 L) = P2(7.00 L)
Solving for P2, we get P2 = 0.714 atm = partial pressure of H2.
Now we do that same thing for the O2:
(1.90 atm)(5.00 L) = P2(7.00 L)P2 = 1.36 atm = partial pressure of O2
The total pressure is the sum of the two resulting partial pressures:
Ptot = 0.714 atm + 1.36 atm = 2.07 atm
If 0.75 atm of He in a 2.00 L container is connected to a 3.00 L container with 0.35 atm of Ne and the containers are opened, what is the resulting total pressure?
- Answer
-
0.51 atm
Dalton’s law states that in a gas mixture (\(P_{total}\)) each gas will exert a pressure independent of the other gases (\(P_n\)) and each gas will behave as if it alone occupies the total volume. By extension, the partial pressure of each gas can be calculated by multiplying the total pressure (\(P_{total}\)) by the gas percentage (%).
\[P_{Total} = P_1 + P_2 + P_3 + P_4 + ... + P_n \nonumber \]
or
\[P_n = \dfrac{\text{% of individual gas}_n}{P_{Total}} \nonumber \]
| Gas | Partial Pressure (mm Hg) | Percentage (%) |
|---|---|---|
| Nitrogen, (N_2\) | \(P_{N_2}\) = 594 | 78 |
| Oxygen, \(O_2\) | \(P_{O_2}\)= 160 | 21 |
| Carbon Dioxide, \(CO_2\) | \(P_{CO_2}\) = 0.25 | 0.033 |
| Water Vapor, \(H_2O\) | \(P_{H_2O}\) = 5.7 | 0.75 |
| Other trace gases | \(P_{Other}\) = 0.05 | 0.22 |
| Total air | \(P_{Total}\) = 760 | 1 |
Application of Dalton's Law: Collecting Gases over Water
A common laboratory method of collecting the gaseous product of a chemical reaction is to conduct it into an inverted tube or bottle filled with water, the opening of which is immersed in a larger container of water. This arrangement is called a pneumatic trough, and was widely used in the early days of chemistry. As the gas enters the bottle it displaces the water and becomes trapped in the upper part.
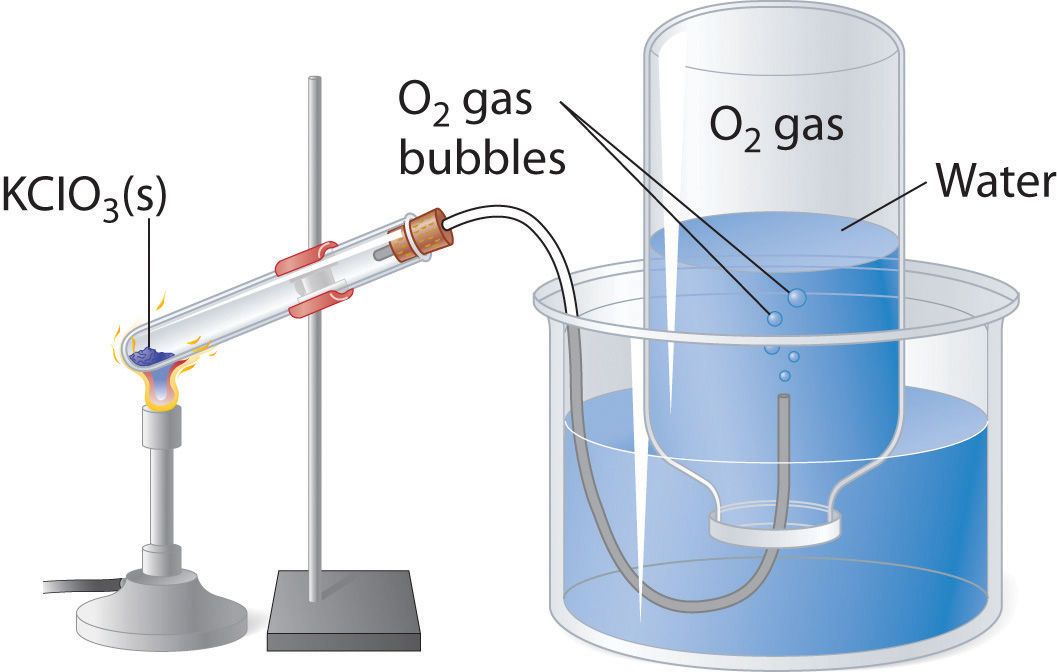
The volume of the gas can be observed by means of a calibrated scale on the bottle, but what about its pressure? The total pressure confining the gas is just that of the atmosphere transmitting its force through the water. (An exact calculation would also have to take into account the height of the water column in the inverted tube.) But liquid water itself is always in equilibrium with its vapor, so the space in the top of the tube is a mixture of two gases: the gas being collected, and gaseous H2O. The partial pressure of H2O is known as the vapor pressure of water and it depends on the temperature. In order to determine the quantity of gas we have collected, we must use Dalton's Law to find the partial pressure of that gas.
Oxygen gas was collected over water as shown above. The atmospheric pressure was 754 torr, the temperature was 22°C, and the volume of the gas was 155 mL. The vapor pressure of water at 22°C is 19.8 torr. Use this information to estimate the number of moles of \(O_2\) produced.
Solution
From Dalton's law,
\[P_{O_2} = P_{total} – P_{H_2O} = 754 – 19.8 = 734 \; torr = 0.966\; atm \nonumber \]
Now use the Ideal Gas Law to convert to moles
\[ n =\dfrac{PV}{RT} = \dfrac{(0.966\; atm)(0.155\;L)}{(0.082\; L atm mol^{-1} K^{-1})(295\; K)}= 0.00619 \; mol \nonumber \]
\(\ce{CO2}\), generated by the decomposition of \(\ce{CaCO3}\), is collected in a 3.50 L container over water. If the temperature is 50°C and the total pressure inside the container is 833 torr, how many moles of \(\ce{CO2}\) were generated?
- Answer
-
0.129 mol
Carbonated beverages—sodas, beer, sparkling wines—have one thing in common: they have \(\ce{CO2}\) gas dissolved in them in such sufficient quantities that it affects the drinking experience. Most people find the drinking experience pleasant—indeed, in the United States alone, over 1.5 × 109 gal of soda are consumed each year, which is almost 50 gal per person! This figure does not include other types of carbonated beverages, so the total consumption is probably significantly higher.
All carbonated beverages are made in one of two ways. First, the flat beverage is subjected to a high pressure of \(\ce{CO2}\) gas, which forces the gas into solution. The carbonated beverage is then packaged in a tightly-sealed package (usually a bottle or a can) and sold. When the container is opened, the \(\ce{CO2}\) pressure is released, resulting in the well-known hiss of an opening container, and \(\ce{CO2}\) bubbles come out of solution. This must be done with care: if the \(\ce{CO2}\) comes out too violently, a mess can occur!

The second way a beverage can become carbonated is by the ingestion of sugar by yeast, which then generates \(\ce{CO2}\) as a digestion product. This process is called fermentation. The overall reaction is
\[\ce{C6H12O6(aq) → 2C2H5OH(aq) + 2CO2(aq)}\nonumber \]
When this process occurs in a closed container, the \(\ce{CO2}\) produced dissolves in the liquid, only to be released from solution when the container is opened. Most fine sparkling wines and champagnes are turned into carbonated beverages this way. Less-expensive sparkling wines are made like sodas and beer, with exposure to high pressures of \(\ce{CO2}\) gas.
Summary
- The pressure of a gas in a gas mixture is termed the partial pressure.
- Dalton's law of partial pressure says that the total pressure in a gas mixture is the sum of the individual partial pressures.


