8.2: Intermolecular Forces

Learning Objective

• Identify the different types of intermolecular forces.
• Relate the physical properties of a substance to the strength of attractive forces.

Why does a substance exist as a solid, liquid, or a gas at specific temperatures? Why do some substances evaporate quickly or melt more easily? These questions can be answered by considering the balance between the energy of the particles and intermolecular forces (or intermolecular interactions) between the particles. If the forces between particles are strong enough, the substance is a liquid or, if stronger, a solid. If the forces between particles are weak and sufficient energy is present, the particles separate from each other, so the gas phase is the preferred phase. The energy of the particles is mostly determined by temperature, so temperature is the main variable that determines what phase is stable at any given point.

There are three types of intermolecular forces: London Dispersion, dipole-dipole, and hydrogen bonding, collectively termed van der Waals forces, that will be introduced below.

London Dispersion Forces

There are forces between all molecules that are caused by electrons being in different places in a molecule at any one time, which sets up a temporary separation of charge (a temporary dipole moment) that disappears almost as soon as it appears. These very weak intermolecular interactions are called dispersion forces (or London dispersion forces, named for the physicist Fritz London, who first described this force in the early 1900s).

Dispersion forces that develop between atoms in different molecules can attract the two molecules to each other. The forces are relatively weak, however, and become significant only when the molecules are very close. Larger and heavier atoms and molecules exhibit stronger dispersion forces than do smaller and lighter atoms and molecules. F₂ and Cl₂ are gases at room temperature (reflecting weaker attractive forces); Br₂ is a liquid, and I₂ is a solid (reflecting stronger attractive forces). Trends in observed melting and boiling points for the halogens clearly demonstrate this effect, as seen in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Melting and Boiling Points of the Halogens

Halogen	Molar Mass	Atomic Radius	Melting Point	Boiling Point
fluorine, F2	38 g/mol	72 pm	53 K	85 K
chlorine, Cl2	71 g/mol	99 pm	172 K	238 K
bromine, Br2	160 g/mol	114 pm	266 K	332 K
iodine, I2	254 g/mol	133 pm	387 K	457 K
astatine, At2	420 g/mol	150 pm	575 K	610 K

The increase in melting and boiling points with increasing atomic/molecular size may be rationalized by considering how the strength of dispersion forces is affected by the electronic structure of the atoms or molecules in the substance. In a larger atom, the valence electrons are, on average, farther from the nuclei than in a smaller atom. Thus, they are less tightly held and can more easily form the temporary dipoles that produce the attraction. The measure of how easy or difficult it is for another electrostatic charge (for example, a nearby ion or polar molecule) to distort a molecule’s charge distribution (its electron cloud) is known as polarizability. A molecule that has a charge cloud that is easily distorted is said to be very polarizable and will have large dispersion forces; one with a charge cloud that is difficult to distort is not very polarizable and will have small dispersion forces.

Example \(\PageIndex{1}\)

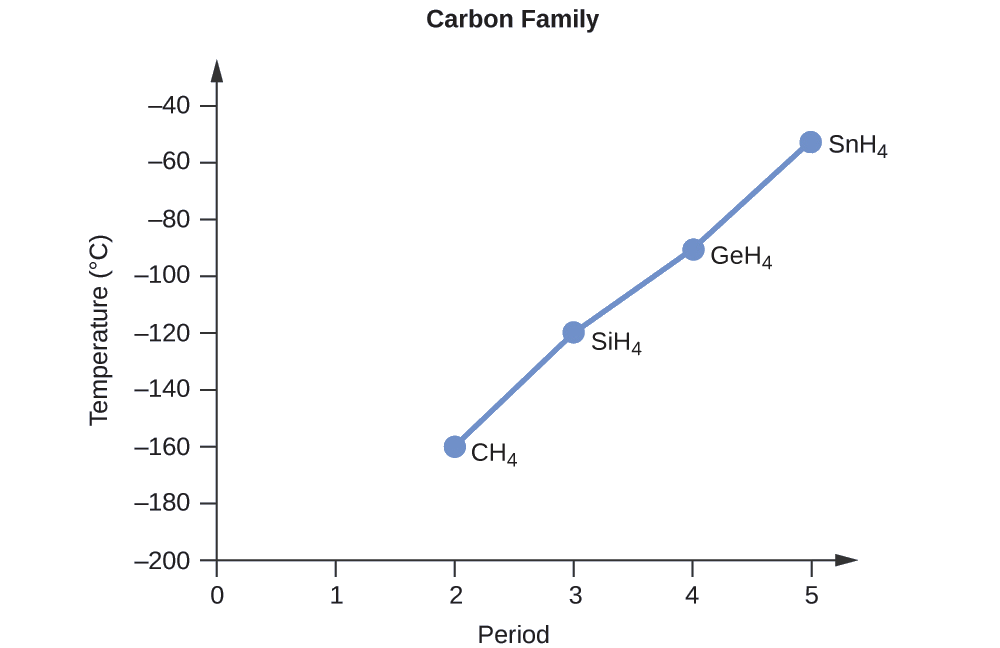
Order the following compounds of a group 14 element and hydrogen from lowest to highest boiling point: CH₄, SiH₄, GeH₄, and SnH₄. Explain your reasoning.

Solution

Applying the skills acquired in the chapter on chemical bonding and molecular geometry, all of these compounds are predicted to be nonpolar, so they may experience only dispersion forces: the smaller the molecule, the less polarizable and the weaker the dispersion forces; the larger the molecule, the larger the dispersion forces. The molar masses of CH₄, SiH₄, GeH₄, and SnH₄ are approximately 16 g/mol, 32 g/mol, 77 g/mol, and 123 g/mol, respectively. Therefore, CH₄ is expected to have the lowest boiling point and SnH₄ the highest boiling point. The ordering from lowest to highest boiling point is expected to be

CH₄ < SiH₄ < GeH₄ < SnH₄

A graph of the actual boiling points of these compounds versus the period of the group 14 elements shows this prediction to be correct:

Exercise \(\PageIndex{1}\)

Order the following hydrocarbons from lowest to highest boiling point: C₂H₆, C₃H₈, and C₄H₁₀.

Answer

All of these compounds are nonpolar and only have London dispersion forces: the larger the molecule, the larger the dispersion forces and the higher the boiling point. The ordering from lowest to highest boiling point is therefore

C₂H₆ < C₃H₈ < C₄H₁₀.

Dipole-Dipole Intermolecular Forces

Recall that a polar molecule will have a net unequal distribution of electrons in its covalent bonds resulting in a partial positive charge on one side of the molecule and a partial negative charge on the other side of the molecule—a separation of charge called a dipole. The electrostatic attraction between oppositely charged ends of polar molecules are called dipole-dipole interactions, (as illustrated in Figure \(\PageIndex{1}\)). Dipole-dipole attractions are between permanent dipoles and are therefore generally stronger than dispersion forces, which are between temporary dipoles. Thus, a polar molecule such as CH₂Cl₂ has a significantly higher boiling point (313 K, or 40°C) than a nonpolar molecule like CF₄ (145 K, or −128°C), even though it has a lower molar mass (85 g/mol vs. 88 g/mol).

Figure \(\PageIndex{1}\): This image illustrates a dipole-dipole interaction, two arrangements of polar molecules that allow an attraction between the partial negative end of one molecule and the partial positive end of another.

Example \(\PageIndex{2}\)

Predict which will have the higher boiling point: N₂ or CO. Explain your reasoning.

Solution

CO and N₂ are both diatomic molecules with masses of about 28 amu, so they experience similar London dispersion forces. Because CO is a polar molecule, it experiences dipole-dipole attractions. Because N₂ is nonpolar, its molecules cannot exhibit dipole-dipole attractions. The dipole-dipole attractions between CO molecules are comparably stronger than the dispersion forces between nonpolar N₂ molecules, so CO is expected to have the higher boiling point.

Exercise \(\PageIndex{2}\)

Predict which will have the higher boiling point: \(\ce{ICl}\) or \(\ce{Br2}\). Explain your reasoning.

Answer

ICl. ICl and Br₂ have similar masses (~160 amu) and therefore experience similar London dispersion forces. ICl is polar and thus also exhibits dipole-dipole attractions; Br₂ is nonpolar and does not. The relatively stronger dipole-dipole attractions require more energy to overcome, so ICl will have the higher boiling point.

Hydrogen Bonds

An unusually strong form of dipole-dipole interaction is called hydrogen bonding. Hydrogen bonding is found in molecules with an H atom bonded to an N atom, an O atom, or an F atom. Such covalent bonds are very polar, and the dipole-dipole interaction between these bonds in two or more molecules is strong enough to create a new category of intermolecular force. Hydrogen bonding is the reason water has unusual properties. For such a small molecule (its molar mass is only 18 g/mol), H₂O has relatively high melting and boiling points. Its boiling point is 373 K (100°C), while the boiling point of a similar molecule, H₂S, is 233 K (−60°C). This is because H₂O molecules experience hydrogen bonding, while H₂S molecules do not. This strong attraction between H₂O molecules requires additional energy to separate the molecules in the condensed phase, so its boiling point is higher than would be expected. Hydrogen bonding is also responsible for water's ability as a solvent, its high heat capacity, and its ability to expand when freezing; the molecules line up in such a way that there is extra space between the molecules, increasing its volume in the solid state (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): Hydrogen Bonding. When water solidifies, hydrogen bonding between the molecules forces the molecules to line up in a way that creates empty space between the molecules, increasing the overall volume of the solid. This is why ice is less dense than liquid water.

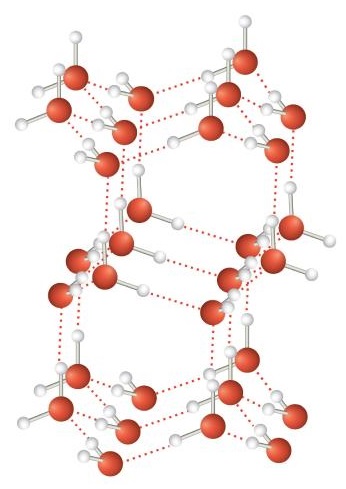
Despite use of the word “bond,” keep in mind that hydrogen bonds are intermolecular attractive forces, not intramolecular attractive forces (covalent bonds). Hydrogen bonds are much weaker than covalent bonds, but are generally much stronger than other dipole-dipole attractions and dispersion forces.

Hydrogen Bonding and DNA

Deoxyribonucleic acid (DNA) is found in every living organism and contains the genetic information that determines the organism’s characteristics, provides the blueprint for making the proteins necessary for life, and serves as a template to pass this information on to the organism’s offspring. A DNA molecule consists of two (anti-)parallel chains of repeating nucleotides, which form its well-known double helical structure, as shown in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): Two separate DNA molecules form a double-stranded helix in which the molecules are held together via hydrogen bonding. (credit: modification of work by Jerome Walker, Dennis Myts)

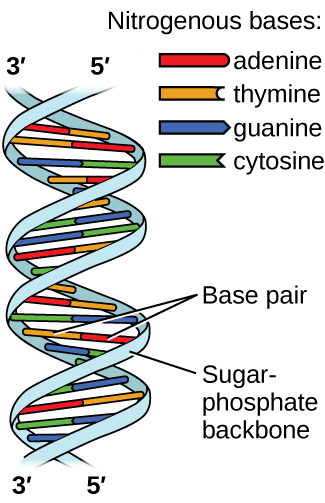
Each nucleotide contains a (deoxyribose) sugar bound to a phosphate group on one side, and one of four nitrogenous bases on the other. Two of the bases, cytosine (C) and thymine (T), are single-ringed structures known as pyrimidines. The other two, adenine (A) and guanine (G), are double-ringed structures called purines. These bases form complementary base pairs consisting of one purine and one pyrimidine, with adenine pairing with thymine, and cytosine with guanine. Each base pair is held together by hydrogen bonding. A and T share two hydrogen bonds, C and G share three, and both pairings have a similar shape and structure Figure \(\PageIndex{4}\)

Figure \(\PageIndex{4}\): The geometries of the base molecules result in maximum hydrogen bonding between adenine and thymine (AT) and between guanine and cytosine (GC), so-called “complementary base pairs.”

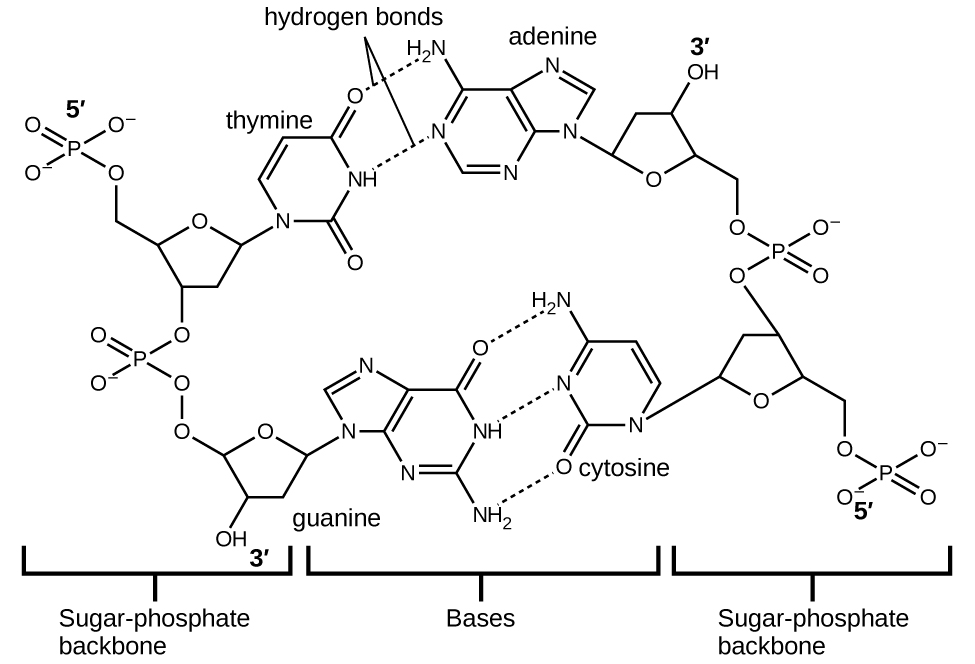
The cumulative effect of millions of hydrogen bonds effectively holds the two strands of DNA together. Importantly, the two strands of DNA can relatively easily “unzip” down the middle since hydrogen bonds are relatively weak compared to the covalent bonds that hold the atoms of the individual DNA molecules together. This allows both strands to function as a template for replication.

Applications: Geckos and Intermolecular Forces

Geckos have an amazing ability to adhere to most surfaces. They can quickly run up smooth walls and across ceilings that have no toe-holds, and they do this without having suction cups or a sticky substance on their toes. And while a gecko can lift its feet easily as it walks along a surface, if you attempt to pick it up, it sticks to the surface. How are geckos (as well as spiders and some other insects) able to do this? Although this phenomenon has been investigated for hundreds of years, scientists only recently uncovered the details of the process that allows geckos’ feet to behave this way.

Figure \(\PageIndex{12}\): Geckos’ toes contain large numbers of tiny hairs (setae), which branch into many triangular tips (spatulae). Geckos adhere to surfaces because of van der Waals attractions between the surface and a gecko’s millions of spatulae. By changing how the spatulae contact the surface, geckos can turn their stickiness “on” and “off.” (credit photo: modification of work by “JC*+A!”/Flickr)

Geckos’ toes are covered with hundreds of thousands of tiny hairs known as setae, with each seta, in turn, branching into hundreds of tiny, flat, triangular tips called spatulae. The huge numbers of spatulae on its setae provide a gecko, shown in Figure 8.1.12, with a large total surface area for sticking to a surface. In 2000, Kellar Autumn, who leads a multi-institutional gecko research team, found that geckos adhered equally well to both polar silicon dioxide and nonpolar gallium arsenide. This proved that geckos stick to surfaces because of dispersion forces—weak intermolecular attractions arising from temporary, synchronized charge distributions between adjacent molecules. Although dispersion forces are very weak, the total attraction over millions of spatulae is large enough to support many times the gecko’s weight.

In 2014, two scientists developed a model to explain how geckos can rapidly transition from “sticky” to “non-sticky.” Alex Greaney and Congcong Hu at Oregon State University described how geckos can achieve this by changing the angle between their spatulae and the surface. Geckos’ feet, which are normally nonsticky, become sticky when a small shear force is applied. By curling and uncurling their toes, geckos can alternate between sticking and unsticking from a surface, and thus easily move across it. Further investigations may eventually lead to the development of better adhesives and other applications.

Boiling Points and Bonding Types

In order for a substance to enter the gas phase, its particles must completely overcome the intermolecular forces holding them together. Therefore, a comparison of boiling points is essentially equivalent to comparing the strengths of the attractive intermolecular forces exhibited by the individual molecules. For small molecular compounds, London dispersion forces are the weakest intermolecular forces. Dipole-dipole forces are somewhat stronger, and hydrogen bonding is a particularly strong form of dipole-dipole interaction. However, when the mass of a nonpolar molecule is sufficiently large, its dispersion forces can be stronger than the dipole-dipole forces in a lighter polar molecule. Thus, nonpolar Cl₂ has a higher boiling point than polar HCl.

Table \(\PageIndex{3}\): Intermolecular Forces and Boiling Points

Substance	Strongest Intermolecular Force	Boiling Point \(\left( ^\text{o} \text{C} \right)\)
\(\ce{H_2}\)	dispersion	-253
\(\ce{Ne}\)	dispersion	-246
\(\ce{O_2}\)	dispersion	-183
\(\ce{Cl_2}\)	dispersion	-34
\(\ce{HCl}\)	dipole-dipole	-85
\(\ce{HBr}\)	dipole-dipole	-66
\(\ce{H_2S}\)	dipole-dipole	-61
\(\ce{NH_3}\)	hydrogen bonding	-33
\(\ce{HF}\)	hydrogen bonding	20
\(\ce{H_2O}\)	hydrogen bonding	100

Example \(\PageIndex{3}\)

Consider the compounds dimethylether (CH₃OCH₃), ethanol (CH₃CH₂OH), and propane (CH₃CH₂CH₃). Their boiling points, not necessarily in order, are −42.1 °C, −24.8 °C, and 78.4 °C. Match each compound with its boiling point. Explain your reasoning.

Solution

The shapes of CH₃OCH₃, CH₃CH₂OH, and CH₃CH₂CH₃ are similar, as are their molar masses (46 g/mol, 46 g/mol, and 44 g/mol, respectively), so they will exhibit similar dispersion forces. Since CH₃CH₂CH₃ is nonpolar, it may exhibit only dispersion forces. Because CH₃OCH₃ is polar, it will also experience dipole-dipole attractions. Finally, CH₃CH₂OH has an −OH group, and so it will experience the uniquely strong dipole-dipole attraction known as hydrogen bonding. So the ordering in terms of strength of IMFs, and thus boiling points, is CH₃CH₂CH₃ < CH₃OCH₃ < CH₃CH₂OH. The boiling point of propane is −42.1 °C, the boiling point of dimethylether is −24.8 °C, and the boiling point of ethanol is 78.5 °C.

Exercise \(\PageIndex{3}\)

Ethane (CH₃CH₃) has a melting point of −183 °C and a boiling point of −89 °C. Predict the melting and boiling points for methylamine (CH₃NH₂). Explain your reasoning.

Answer

The melting point and boiling point for methylamine are predicted to be significantly greater than those of ethane. CH₃CH₃ and CH₃NH₂ are similar in size and mass, but methylamine possesses an −NH group and therefore may exhibit hydrogen bonding. This greatly increases its IMFs, and therefore its melting and boiling points. It is difficult to predict values, but the known values are a melting point of −93 °C and a boiling point of −6 °C.

Example \(\PageIndex{4}\): Intermolecular Forces

What intermolecular forces besides dispersion forces, if any, exist in each substance? Are any of these substances solids at room temperature?

1. potassium chloride (KCl)
2. ethanol (C₂H₅OH)
3. bromine (Br₂)

Solution

1. Potassium chloride is composed of ions, so the intermolecular interaction in potassium chloride is ionic forces. Because ionic interactions are strong, it might be expected that potassium chloride is a solid at room temperature.
2. Ethanol has a hydrogen atom attached to an oxygen atom, so it would experience hydrogen bonding. If the hydrogen bonding is strong enough, ethanol might be a solid at room temperature, but it is difficult to know for certain. (Ethanol is actually a liquid at room temperature.)
3. Elemental bromine has two bromine atoms covalently bonded to each other. Because the atoms on either side of the covalent bond are the same, the electrons in the covalent bond are shared equally, and the bond is a nonpolar covalent bond. Thus, diatomic bromine does not have any intermolecular forces other than dispersion forces. It is unlikely to be a solid at room temperature unless the dispersion forces are strong enough. Bromine is a liquid at room temperature.

Exercise \(\PageIndex{4}\)

What intermolecular forces besides dispersion forces, if any, exist in each substance? Are any of these substances solids at room temperature?

1. methylamine (CH₃NH₂)
2. calcium sulfate (CaSO₄)
3. carbon monoxide (CO)

Answer

a. dipole-dipole, hydrogen bonding

b. ionic forces (solid at room temperature)

c. dipole-dipole

Concept Review Exercise

1. What types of intermolecular interactions can exist in compounds?

2. What is the difference between covalent network and covalent molecular compounds?

Answer

1. ionic bonding, network covalent, dispersion forces, dipole-dipole interactions, and hydrogen bonding.

2. Covalent network compounds contain atoms that are covalently bonded to other individual atoms in a giant 3-dimensional network. Covalent molecular compounds contain individual molecules that are attracted to one another through dispersion, dipole-dipole or hydrogen bonding.

Key Takeaways

• A phase is a form of matter that has the same physical properties throughout.
• Molecules interact with each other through various forces: dipole-dipole interactions, hydrogen bonding, and dispersion forces.
• Dipole-dipole attractions result from the electrostatic attraction of the partial negative end of one dipolar molecule for the partial positive end of another.
• Hydrogen bonds are a special type of dipole-dipole attraction that results when hydrogen is bonded to one of the three most electronegative elements: F, O, or N.
• The temporary dipole that results from the motion of the electrons in an atom can induce a dipole in an adjacent atom and give rise to the London dispersion force. London forces increase with increasing molecular size.

Exercises

1. List the three common phases in the order you are likely to find them—from lowest temperature to highest temperature.

2. List the three common phases in the order they exist from lowest energy to highest energy.

3. List these intermolecular interactions from weakest to strongest: London forces, hydrogen bonding, and ionic interactions.

4. List these intermolecular interactions from weakest to strongest: covalent network bonding, dipole-dipole interactions, and dispersion forces.

5. What type of intermolecular interaction is predominate in each substance?

   1. water (H₂O)
   2. sodium sulfate (Na₂SO₄)
   3. decane (C₁₀H₂₂)

6. What type of intermolecular interaction is predominate in each substance?

   1. diamond (C, crystal)
   2. helium (He)
   3. ammonia (NH₃)

7. Explain how a molecule like carbon dioxide (CO₂) can have polar covalent bonds but be nonpolar overall.

8. Sulfur dioxide (SO₂) has a formula similar to that of carbon dioxide (see Exercise 7) but is a polar molecule overall. What can you conclude about the shape of the SO₂ molecule?

9. What are some of the physical properties of substances that experience covalent network bonding?

10. What are some of the physical properties of substances that experience only dispersion forces?

Answers

1. solid, liquid, and gas

2. solid, liquid, and gas

3. London forces, hydrogen bonding, and ionic interactions

4. dispersion, dipole-dipole, network covalent

5. 1. hydrogen bonding
   2. ionic interactions
   3. dispersion forces

6. a. network covalent

b. dispersion

c. hydrogen bonding

7. The two covalent bonds are oriented in such a way that their dipoles cancel out.

8. SO₂ is not a linear molecule. It has a bent or V-shape.

9. very hard, high melting point

10. very soft, very low melting point