7.6: The pH Scale
- Page ID
- 152180
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define \(pH\).
- Determine the pH of acidic and basic solutions.
- Determine the hydrogen (hydronium) ion concentration from pH and vice versa.
Molar concentration values of hydrogen \([H^+]\) can be markedly different from one aqueous solution to another. So chemists defined a new scale that succinctly indicates the concentrations of either of these two ions. This is known as the \(pH\) scale. The range of values from 0 to 14 that describes the acidity or basicity of a solution. You can use \(pH\) to make a quick determination whether a given aqueous solution is acidic, basic, or neutral.
pH is a logarithmic scale. A solution that has a pH of 1.0 has 10 times the [H+] as a solution with a pH of 2.0, which in turn has 10 times the [H+] as a solution with a pH of 3.0 and so forth.
pH is usually (but not always) between 0 and 14. Knowing the dependence of pH on \([H+]\), we can summarize as follows:
- If pH < 7, then the solution is acidic.
- If pH = 7, then the solution is neutral.
- If pH > 7, then the solution is basic.

Figure \(\PageIndex{2}\) illustrates the relationship between pH and the hydrogen ion concentration, along with some examples of various solutions. Because hydrogen ion concentrations are generally less than one (for example \(1.3 \times 10^{-3}\,M\)), the log of the number will be a negative number. To make pH even easier to work with, pH is defined as the negative log of \([H^+]\), which will give a positive value for pH.
The general formula for determining [H+] from pH is as follows:
[H+] = 10−pH
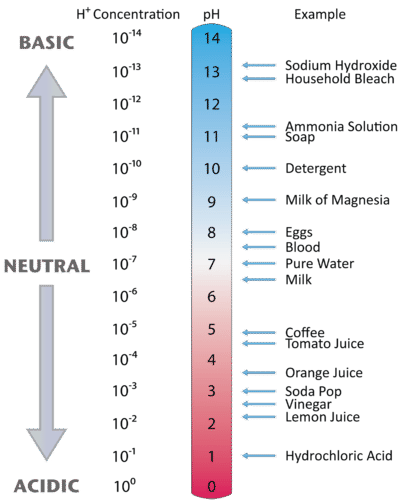
Label each solution as acidic, basic, or neutral based only on the stated \(pH\).
- milk of magnesia, pH = 10.5
- pure water, pH = 7
- wine, pH = 3.0
Answer
- With a pH greater than 7, milk of magnesia is basic. (Milk of magnesia is largely Mg(OH)2.)
- Pure water, with a pH of 7, is neutral.
- With a pH of less than 7, wine is acidic.
Identify each substance as acidic, basic, or neutral based only on the stated \(pH\).
- human blood with \(pH\) = 7.4
- household ammonia with \(pH\) = 11.0
- cherries with \(pH\) = 3.6
- Answer a
- basic
- Answer b
- basic
- Answer c
- acidic
| Substance | pH |
|---|---|
| stomach acid | 1.7 |
| lemon juice | 2.2 |
| vinegar | 2.9 |
| soda | 3.0 |
| wine | 3.5 |
| coffee, black | 5.0 |
| milk | 6.9 |
| pure water | 7.0 |
| blood | 7.4 |
| seawater | 8.5 |
| milk of magnesia | 10.5 |
| ammonia solution | 12.5 |
| 1.0 M NaOH | 14.0 |
| *Actual values may vary depending on conditions | |
What is the [H+] for an aqueous solution whose pH is 6?
Solution
The pH value of 6 denotes that the exponent of 10 is -6. Therefore the answer is
[H+] = 1.0 x 10−6M
What is the [H+] for an aqueous solution whose pH is 11?
Answer
[H+] = 1.0 × 10−11 M
What is the pH of an aqueous solution whose hydrogen ion concentration is 1.0 x 10−7M? Is the solution acidic, basic, or neutral.
Solution
The hydrogen ion concentration is 1.0 x 10−7M. The exponent of 10 is -7, which denoted that pH= -(-7) = 7. The solution is neutral.
What is the pH of an aqueous solution whose hydrogen ion concentration is 1.0 x 10−3M? Is the solution acidic, basic, or neutral.
Solution
The hydrogen ion concentration is 1.0 x 10−3M. The exponent of 10 is -3, which denoted that pH= -(-3) = 3. The solution is acidic.
Summary
To make pH even easier to work with, pH is defined as the negative log of \([H^+]\), which will give a positive value for pH.
pH is usually (but not always) between 0 and 14.
- If pH < 7, then the solution is acidic.
- If pH = 7, then the solution is neutral.
- If pH > 7, then the solution is basic.
Contributors and Attributions
Peggy Lawson (Oxbow Prairie Heights School). Funded by Saskatchewan Educational Technology Consortium.
- Template:OpenStax
Henry Agnew (UC Davis)

