6.6: The Simple Gas Laws
- Page ID
- 152173
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Learn what is meant by the term gas laws.
- Know the different units of pressure.
- Learn and apply Boyle’s law.
- Learn and apply Charles's law.
- Learn and apply Gay-Lussac's law.
The behavior of gases can be modeled with gas laws. Boyle’s law relates a gas’s pressure and volume at constant temperature and amount. Charles’s law relates a gas’s volume and temperature at constant pressure and amount. In gas laws, temperatures must always be expressed in Kelvins.
A barometer measures gas pressure by the height of the column of mercury. One unit of gas pressure is the millimeter of mercury \(\left( \text{mm} \: \ce{Hg} \right)\). An equivalent unit to the \(\text{mm} \: \ce{Hg}\) is called the \(\text{torr}\), in honor of the inventor of the barometer, Evangelista Torricelli. The pascal \(\left( \text{Pa} \right)\) is the standard unit of pressure. A pascal is a very small amount of pressure, so the most useful unit for everyday gas pressures is the kilopascal \(\left( \text{kPa} \right)\). A kilopascal is equal to 1000 pascals. Another commonly used unit of pressure is the atmosphere \(\left( \text{atm} \right)\). Standard atmospheric pressure is called \(1 \: \text{atm}\) of pressure and is equal to \(760 \: \text{mm} \: \ce{Hg}\) and \(101.3 \: \text{kPa}\). Atmospheric pressure is also often stated as pounds per square inch \(\left( \text{psi} \right)\). The atmospheric pressure at sea level is \(14.7 \: \text{psi}\).
\[1 \: \text{atm} = 760 \: \text{mm} \: \ce{Hg} = 760 \: \text{torr} = 101.3 \: \text{kPa} = 14.7 \: \text{psi} \nonumber \]
Boyle's Law: Pressure and Volume
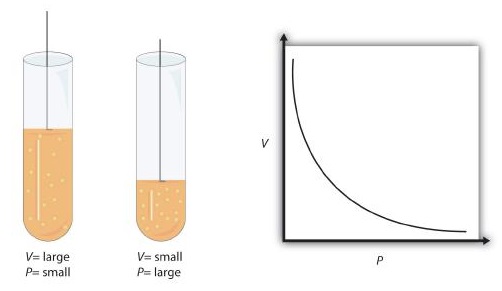
When seventeenth-century scientists began studying the physical properties of gases, they noticed some simple relationships between some of the measurable properties of the gas. Take pressure (P) and volume (V), for example. Scientists noted that for a given amount of a gas (usually expressed in units of moles [n]), if the temperature (T) of the gas was kept constant, pressure and volume were related: As one increases, the other decreases. As one decreases, the other increases. We say that pressure and volume are inversely related.
There is more to it, however: pressure and volume of a given amount of gas at constant temperature are numerically related. If you take the pressure value and multiply it by the volume value, the product is a constant for a given amount of gas at a constant temperature:
\[P × V = \text{ constant at constant n and T} \nonumber \]
If either volume or pressure changes while amount and temperature stay the same, then the other property must change so that the product of the two properties still equals that same constant. That is, if the original conditions are labeled \(P_1\) and \(V_1\) and the new conditions are labeled \(P_2\) and \(V_2\), we have
\[P_1V_1 = \text{constant} = P_2V_2 \nonumber \]
where the properties are assumed to be multiplied together. Leaving out the middle part, we have simply
\[P_1V_1 = P_2V_2 \text{ at constant n and T} \nonumber \]
This equation is an example of a gas law. A gas law is a simple mathematical formula that allows you to model, or predict, the behavior of a gas. This particular gas law ia called Boyle's law, after the English scientist Robert Boyle, who first announced it in 1662. Figure \(\PageIndex{1}\) shows two representations of how Boyle’s law works.
Boyle’s law is an example of a second type of mathematical problem we see in chemistry—one based on a mathematical formula. Tactics for working with mathematical formulas are different from tactics for working with conversion factors. First, most of the questions you will have to answer using formulas are word-type questions, so the first step is to identify what quantities are known and assign them to variables. Second, in most formulas, some mathematical rearrangements (i.e., algebra) must be performed to solve for an unknown variable. The rule is that to find the value of the unknown variable, you must mathematically isolate the unknown variable by itself and in the numerator of one side of the equation. Finally, units must be consistent. For example, in Boyle’s law there are two pressure variables; they must have the same unit. There are also two volume variables; they also must have the same unit. In most cases, it won’t matter what the unit is, but the unit must be the same on both sides of the equation.
A sample of gas has an initial pressure of 2.44 atm and an initial volume of 4.01 L. Its pressure changes to 1.93 atm. What is the new volume if temperature and amount are kept constant?
Solution
Steps for Problem Solving |
Example \(\PageIndex{1}\) |
|---|---|
| Identify the "given"information and what the problem is asking you to "find." |
Given: P1 = 2.44 atm and V1 = 4.01 L P2 = 1.93 atm Find: V2 = ? L |
| List other known quantities. | none |
| Plan the problem. |
First, rearrange the equation algebraically to solve for \(V_2\). \[V_2 = \frac{P_1 \times V_1}{P_2} \nonumber \] |
| Cancel units and calculate. |
Now substitute the known quantities into the equation and solve. \[V_2 = \frac{2.44 \: \cancel{\text{atm}} \times 4.01 \: \text{L}}{1.93 \: \cancel{atm}} = 5.07 \: \text{L} \nonumber \] |
| Think about your result. | We know that pressure and volume are inversely related; as one decreases, the other increases. Pressure is decreasing (from 2.44 atm to 1.93 atm), so volume should be increasing to compensate, and it is (from 4.01 L to 5.07 L). So the answer makes sense based on Boyle’s law. |
If P1 = 334 torr, V1 = 37.8 mL, and P2 = 102 torr, what is V2?
- Answer
-
124 mL
As mentioned, you can use any units for pressure or volume, but both pressures must be expressed in the same units, and both volumes must be expressed in the same units.
A sample of gas has an initial pressure of 722 torr and an initial volume of 88.8 mL. Its volume changes to 0.663 L. What is the new pressure?
Solution
Steps for Problem Solving |
Example \(\PageIndex{2}\) |
|---|---|
| Identify the "given"information and what the problem is asking you to "find." |
Given: P1 = 722 torr and V1 = 88.8 mL V2 = 0.633 L Find: P2 = ? torr |
| List other known quantities. | 1 L = 1000 mL to have the same units for volume. |
| Plan the problem. |
1. Perform the conversion of the second volume unit from L to mL. 2. Rearrange the equation algebraically to solve for \(P_2\). \[P_2 = \frac{P_1 \times V_1}{V_2} \nonumber \] |
| Cancel units and calculate. |
1. \[0.663\, \cancel{L}\times \frac{1000\, ml}{1\, \cancel{L}}=663\, ml \nonumber \] 2. Substitute the known quantities into the equation and solve. \[P_2 = \frac{722 \: \text{torr} \times 88.8 \: \cancel{\text{mL}}}{663 \: \cancel{\text{mL}}} = 96.7 \: \text{torr} \nonumber \] |
| Think about your result. | When the volume increased, the pressure decreased, which is as expected for Boyle’s law. |
If V1 = 456 mL, P1 = 308 torr, and P2 = 1.55 atm, what is V2?
- Answer
-
119 mL
Charles's Law: Temperature and Volume
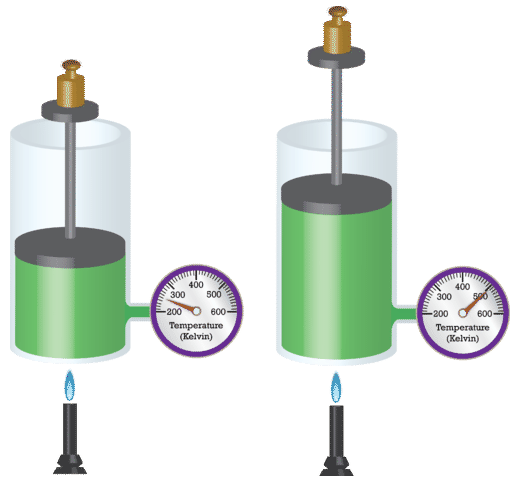
French physicist Jacques Charles (1746 - 1823) studied the effect of temperature on the volume of a gas at constant pressure. Charles's Law states that the volume of a given mass of gas varies directly with the absolute temperature of the gas when pressure is kept constant. The absolute temperature is temperature measured with the Kelvin scale. The Kelvin scale must be used because zero on the Kelvin scale corresponds to a complete stoppage of molecular motion.
Mathematically, the direct relationship of Charles's Law can be represented by the following equation:
\[\frac{V}{T} = k \nonumber \]
As with Boyle's Law, \(k\) is constant only for a given gas sample. The table below shows temperature and volume data for a set amount of gas at a constant pressure. The third column is the constant for this particular data set and is always equal to the volume divided by the Kelvin temperature.
| Temperature \(\left( \text{K} \right)\) | Volume \(\left( \text{mL} \right)\) | \(\frac{V}{T} = k\) \(\left( \frac{\text{mL}}{\text{K}} \right)\) |
|---|---|---|
| 50 | 20 | 0.40 |
| 100 | 40 | 0.40 |
| 150 | 60 | 0.40 |
| 200 | 80 | 0.40 |
| 300 | 120 | 0.40 |
| 500 | 200 | 0.40 |
| 1000 | 400 | 0.40 |
When this data is graphed, the result is a straight line, indicative of a direct relationship, shown in the figure below.
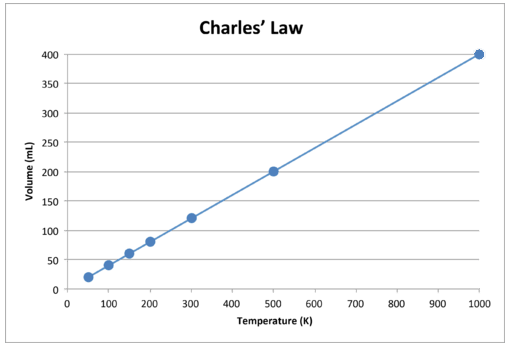
Notice that the line goes exactly toward the origin, meaning that as the absolute temperature of the gas approaches zero, its volume approaches zero. However, when a gas is brought to extremely cold temperatures, its molecules would eventually condense into the liquid state before reaching absolute zero. The temperature at which this change into the liquid state occurs varies for different gases.
Charles's Law can also be used to compare changing conditions for a gas. Now we use \(V_1\) and \(T_1\) to stand for the initial volume and temperature of a gas, while \(V_2\) and \(T_2\) stand for the final volume and temperature. The mathematical relationship of Charles's Law becomes:
\[\frac{V_1}{T_1} = \frac{V_2}{T_2} \nonumber \]
This equation can be used to calculate any one of the four quantities if the other three are known. The direct relationship will only hold if the temperatures are expressed in Kelvin. Temperatures in Celsius will not work. Recall the relationship that \(\text{K} = \: ^\text{o} \text{C} + 273\).
A balloon is filled to a volume of \(2.20 \: \text{L}\) at a temperature of \(22^\text{o} \text{C}\). The balloon is then heated to a temperature of \(71^\text{o} \text{C}\). Find the new volume of the balloon.
Solution
Steps for Problem Solving |
Example\(\PageIndex{3}\) |
|---|---|
| Identify the "given"information and what the problem is asking you to "find." |
Given: \(V_1 = 2.20 \: \text{L}\) and \(T_1 = 22^\text{o} \text{C} = 295 \: \text{K}\) \(T_2 = 71^\text{o} \text{C} = 344 \: \text{K}\) Find: V2 = ? L |
| List other known quantities. | The temperatures have first been converted to Kelvin. |
| Plan the problem. |
First, rearrange the equation algebraically to solve for \(V_2\). \[V_2 = \frac{V_1 \times T_2}{T_1} \nonumber \] |
| Cancel units and calculate. |
Now substitute the known quantities into the equation and solve. \[V_2 = \frac{2.20 \: \text{L} \times 344 \: \cancel{\text{K}}}{295 \: \cancel{\text{K}}} = 2.57 \: \text{L} \nonumber \] |
| Think about your result. | The volume increases as the temperature increases. The result has three significant figures. |
If V1 = 3.77 L and T1 = 255 K, what is V2 if T2 = 123 K?
- Answer
-
1.82 L
A sample of a gas has an initial volume of 34.8 L and an initial temperature of −67°C. What must be the temperature of the gas for its volume to be 25.0 L?
Solution
Steps for Problem Solving |
Example \(\PageIndex{4}\) |
|---|---|
| Identify the "given"information and what the problem is asking you to "find." |
Given: Given:T1 = -27oC and V1 = 34.8 L V2 = 25.0 L Find: T2 = ? K |
| List other known quantities. | K = -27oC + 273 |
| Plan the problem. |
1. Convert the initial temperature to Kelvin 2. Rearrange the equation algebraically to solve for \(T_2\). \[T_2 = \frac{V_2 \times T_1}{V_1} \nonumber \] |
| Cancel units and calculate. |
1. −67°C + 273 = 206 K 2. Substitute the known quantities into the equation and solve. \[T_2 = \frac{25.0 \: \cancel{\text{L}} \times 206 \: \text{K}}{34.8 \: \cancel{\text{L}}} = 148 \: \text{K} \nonumber \] |
| Think about your result. | This is also equal to −125°C. As temperature decreases, volume decreases, which it does in this example. |
If V1 = 623 mL, T1 = 255°C, and V2 = 277 mL, what is T2?
- Answer
-
235 K, or −38°
Gay-Lussac's Law: Temperature and Pressure
When the temperature of a sample of gas in a rigid container is increased, the pressure of the gas increases as well. The increase in kinetic energy results in the molecules of gas striking the walls of the container with more force, resulting in a greater pressure. The French chemist Joseph Gay-Lussac (1778 - 1850) discovered the relationship between the pressure of a gas and its absolute temperature. Gay-Lussac's Law states that the pressure of a given mass of gas varies directly with the absolute temperature of the gas, when the volume is kept constant. Gay-Lussac's Law is very similar to Charles's Law, with the only difference being the type of container. Whereas the container in a Charles's Law experiment is flexible, it is rigid in a Gay-Lussac's Law experiment.

The mathematical expressions for Gay-Lussac's Law are likewise similar to those of Charles's Law:
\[\frac{P}{T} \: \: \: \text{and} \: \: \: \frac{P_1}{T_1} = \frac{P_2}{T_2} \nonumber \]
A graph of pressure vs. temperature also illustrates a direct relationship. As a gas is cooled at constant volume its pressure continually decreases until the gas condenses to a liquid.
The gas in an aerosol can is under a pressure of \(3.00 \: \text{atm}\) at a temperature of \(25^\text{o} \text{C}\). It is dangerous to dispose of an aerosol can by incineration. What would the pressure in the aerosol can be at a temperature of \(845^\text{o} \text{C}\)?
Solution
Steps for Problem Solving |
Example \(\PageIndex{5}\) |
|---|---|
| Identify the "given"information and what the problem is asking you to "find." |
Given: \(P_1 = 3.00 \: \text{atm}\) \(T_1 = 25^\text{o} \text{C} = 298 \: \text{K}\) \(T_2 = 845^\text{o} \text{C} = 1118 \: \text{K}\) Find: \(P_2 = ? \: \text{atm}\) |
| List other known quantities | The temperatures have first been converted to Kelvin. |
| Plan the problem |
First, rearrange the equation algebraically to solve for \(P_2\). \[P_2 = \frac{P_1 \times T_2}{T_1} \nonumber \] |
| Calculate |
Now substitute the known quantities into the equation and solve. \[P_2 = \frac{3.00 \: \text{atm} \times 1118 \: \cancel{\text{K}}}{298 \: \cancel{\text{K}}}= 11.3 \: \text{atm} \nonumber \] |
| Think about your result. | The pressure increases dramatically due to large increase in temperature. |
Molar Volume
It should be obvious by now that some physical properties of gases depend strongly on the conditions. What we need is a set of standard conditions so that properties of gases can be properly compared to each other. Standard Temperature and Pressure (STP) is defined as exactly 100 kPa of pressure (0.986 atm) and 273 K (0°C). For simplicity, we will use 1 atm as standard pressure. Defining STP allows us to compare more directly the properties of gases that differ from each other.
One property shared among gases is a molar volume. The molar volume is the volume of 1 mol of a gas. At STP, the molar volume of a gas can be easily determined by using the ideal gas law:
\[(1\, atm)V=(1\, mol)(0.08205\frac{L.atm}{mol.K})(273\, K) \nonumber \]
All the units cancel except for L, the unit of volume. So V = 22.4 L
Note that we have not specified the identity of the gas; we have specified only that the pressure is 1 atm and the temperature is 273 K. This makes for a very useful approximation: any gas at STP has a volume of 22.4 L per mole of gas; that is, the molar volume at STP is 22.4 L/mol (Fig. 6.6.1 Molar Volume). This molar volume makes a useful conversion factor in stoichiometry problems if the conditions are at STP. If the conditions are not at STP, a molar volume of 22.4 L/mol is not applicable. However, if the conditions are not at STP, the combined gas law can be used to calculate what the volume of the gas would be if at STP; then the 22.4 L/mol molar volume can be used.
How many moles of Ar are present in 38.7 L at STP?
Solution
We can use the molar volume, 22.4 L/mol, as a conversion factor, but we need to reverse the fraction so that the L units cancel and mol units are introduced. It is a one-step conversion:
\[38.7\, \not{L}\times \frac{1\, mol}{22.4\not{L}}=1.73\, mol \nonumber \]
What volume does 4.87 mol of Kr have at STP?
109 L
Chemistry Is Everywhere: Breathing
Breathing (more properly called respiration) is the process by which we draw air into our lungs so that our bodies can take up oxygen from the air. Let us apply the gas laws to breathing.
Start by considering pressure. We draw air into our lungs because the diaphragm, a muscle underneath the lungs, moves down to reduce pressure in the lungs, causing external air to rush in to fill the lower-pressure volume. We expel air by the diaphragm pushing against the lungs, increasing pressure inside the lungs and forcing the high-pressure air out. What are the pressure changes involved? A quarter of an atmosphere? A tenth of an atmosphere? Actually, under normal conditions, it’s only 1 or 2 torr of pressure difference that makes us breathe in and out.
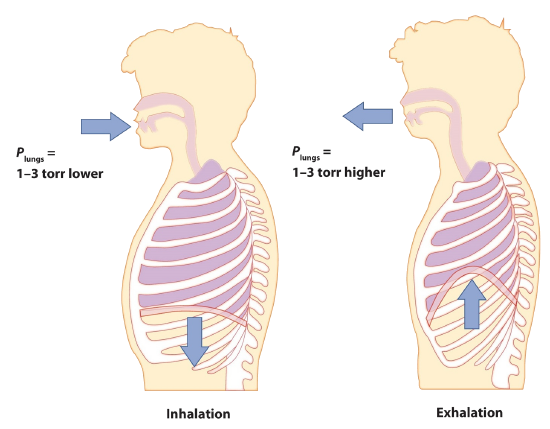
A normal breath is about 0.50 L. If room temperature is about 22°C, then the air has a temperature of about 295 K. With normal pressure being 1.0 atm, how many moles of air do we take in for every breath? The ideal gas law gives us an answer:
\[(1.0\, atm)(0.50\, L)=n(0.08205\frac{L.atm}{mol.K})(295\, K) \nonumber \]
Solving for the number of moles, we get
n = 0.021 mol airThis ends up being about 0.6 g of air per breath—not much but enough to keep us alive.
Summary
- The behavior of gases can be modeled with gas laws.
- Boyle’s law relates a gas’s pressure and volume at constant temperature and amount.
- Charles’s law relates a gas’s volume and temperature at constant pressure and amount.
- Gay-Lussac's Law states that the pressure of a given mass of gas varies directly with the absolute temperature of the gas, when the volume is kept constant.
- In gas laws, temperatures must always be expressed in Kelvins.
Contributors and Attributions
Henry Agnew (UC Davis)

