5.3: Avogadro's Number and the Mole
- Page ID
- 152163
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use Avogadro's number to convert to moles and vice versa given the number of particles of an element.
- Know the definition of the mole.
- Determine the formula mass of an ionic or molecular compound.
- Determine the percent composition of each element in a compound from the chemical formula.
When objects are very small, it is often inconvenient or inefficient, or even impossible to deal with the objects one at a time. For these reasons, we often deal with very small objects in groups, and have even invented names for various numbers of objects. The most common of these is "dozen" which refers to 12 objects. We frequently buy objects in groups of 12, like doughnuts or pencils. Even smaller objects such as straight pins or staples are usually sold in boxes of 144, or a dozen dozen. A group of 144 is called a "gross".
This problem of dealing with things that are too small to operate with as single items also occurs in chemistry. Atoms and molecules are too small to see, let alone to count or measure. Chemists needed to select a group of atoms or molecules that would be convenient to operate with.
Avogadro's Number:Counting Atoms
Owing to their tiny size, atoms and molecules cannot be counted by direct observation. But much as we do when "counting" beans in a jar, we can estimate the number of particles in a sample of an element or compound if we have some idea of the volume occupied by each particle and the volume of the container. Once this has been done, we know the number of formula units (to use the most general term for any combination of atoms we wish to define) in any arbitrary weight of the substance. The number will of course depend both on the formula of the substance and on the weight of the sample. However, if we consider a weight of substance that is the same as its formula (molecular) weight expressed in grams, we have only one number to know: Avogadro's number.
Avogadro's number is known to ten significant digits:
\[N_A = 6.022141527 \times 10^{23}. \nonumber \]
However, you only need to know it to three significant figures:
\[N_A \approx 6.02 \times 10^{23}. \label{3.2.1} \]
So \(6.02 \times 10^{23}\) of what? Well, of anything you like: apples, stars in the sky, burritos. However, the only practical use for \(N_A\) is to have a more convenient way of expressing the huge numbers of the tiny particles such as atoms or molecules that we deal with in chemistry. Avogadro's number is a collective number, just like a dozen. Students can think of \(6.02 \times 10^{23}\) as the "chemist's dozen".
Before getting into the use of Avogadro's number in problems, take a moment to convince yourself of the reasoning embodied in the following examples.
- It is a number, just as is "dozen", and thus is dimensionless.
- It is a huge number, far greater in magnitude than we can visualize
- Its practical use is limited to counting tiny things like atoms, molecules, "formula units", electrons, or photons.
- The value of NA can be known only to the precision that the number of atoms in a measurable weight of a substance can be estimated. Because large numbers of atoms cannot be counted directly, a variety of ingenious indirect measurements have been made involving such things as Brownian motion and X-ray scattering.
The Mole: "A Dozen Eggs and a Mole of Sugar, Please"
The mole (symbol: mol) is the base unit of amount of substance ("number of substance") in the International System of Units or System International (SI), defined as exactly 6.02214076×1023 particles, e.g., atoms, molecules, ions or electrons. The current definition was adopted in November 2018, revising its old definition based on the number of atoms in 12 grams of carbon-12 (12C) (the isotope of carbon with relative atomic mass 12 Daltons by definition).
It is not obvious why eggs come in dozens rather than 10s or 14s, or why a ream of paper contains 500 sheets rather than 400 or 600. The definition of a mole—that is, the decision to base it on 12 g of carbon-12—is also arbitrary. The important point is that 1 mole of carbon—or of anything else, whether atoms, compact discs, or houses—always has the same number of objects: 6.02 × 1023.
Video \(\PageIndex{1}\) How big is a mole?
Converting Between Number of Atoms to Moles and Vice Versa
We can use Avogadro's number as a conversion factor, or ratio, in dimensional analysis problems. If we are given the number of atoms of an element X, we can convert it into moles of by using the relationship
\[\text{1 mol X} = 6.022 \times 10^{23} \text{ X atoms}. \nonumber \]
An example on the use of Avogadro's number as a conversion factor is given below for carbon.
The element carbon exists in two primary forms: graphite and diamond. How many moles of carbon atoms is \(4.72 \times 10^{24}\) atoms of carbon?
Solution
| Steps for Problem Solving | Example |
|---|---|
| Identify the "given"information and what the problem is asking you to "find." | Given: \(4.72 \times 10^{24}\) C atoms Find: mol C |
| List other known quantities | \(1\, mol = 6.022 \times 10^{23}\) C atoms |
| Prepare a concept map and use the proper conversion factor. | |
| Cancel units and calculate. | \[4.72 \times 10^{24} \: \cancel{\text{C} \: \ce{atoms}} \times \frac{1 \: \text{mol} \: \ce{C}}{6.02 \times 10^{23} \: \cancel{\text{C} \: \ce{atoms}}} = 7.84 \: \text{mol} \: \ce{C} \nonumber \] |
| Think about your result. | The given number of carbon atoms was greater than Avogadro's number,so the number of moles of \(\ce{C}\) atoms is greater than 1 mole. Since Avogadro's number is a measured quantity with three significant figures, the result of the calculation is rounded to three significant figures |
Formula Mass
One skill needed in future chapters is the ability to determine the mass of the formula of various chemical substances. This quantity is called the formula mass. The formula mass is obtained by adding the masses of each individual atom in the formula of the substance. Because a proper formula is electrically neutral (with no net electrons gained or lost), the ions can be considered atoms for the purpose of calculating the formula mass.
Let us start by calculating the formula mass of sodium chloride (NaCl). This formula mass is the sum of the atomic masses of one sodium atom and one chlorine atom, which we find from the periodic table; here, we use the masses to two decimal places:
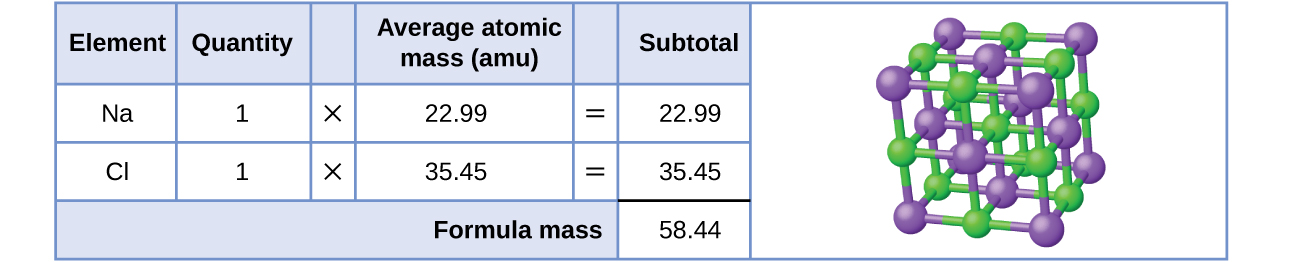
To two decimal places, the formula mass of NaCl is 58.44 amu.
For covalent substances, the formula represents the numbers and types of atoms composing a single molecule of the substance; therefore, the formula mass may be correctly referred to as a molecular mass. Consider chloroform (CHCl3), a covalent compound once used as a surgical anesthetic and now primarily used in the production of tetrafluoroethylene, the building block for the “anti-stick” polymer, Teflon. The molecular formula of chloroform indicates that a single molecule contains one carbon atom, one hydrogen atom, and three chlorine atoms. The average molecular mass of a chloroform molecule is therefore equal to the sum of the average atomic masses of these atoms.
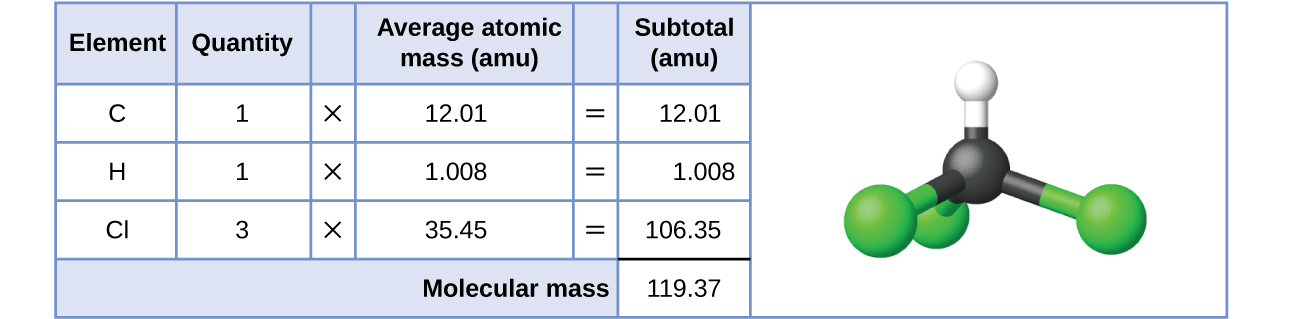
To two decimal places, the formula mass of CHCl3 is 119.37 amu.
For ionic compounds with polyatomic ions, the sum must include the number and mass of each atom in the formula for the polyatomic ion. as shown in the example below for aluminum sulfate, Al2(SO4)3.
Aluminum sulfate, Al2(SO4)3, is an ionic compound that is used in the manufacture of paper and in various water purification processes. What is the formula mass (amu) of this compound?
Solution
The formula for this compound indicates it contains Al3+ and SO42− ions combined in a 2:3 ratio. For purposes of computing a formula mass, it is helpful to rewrite the formula in the simpler format, Al2S3O12. Following the approach outlined above, the formula mass for this compound is calculated as follows:

The formula mass for Al2(SO4)3, is 342.14 amu.
Use the atomic masses (rounded to two decimal places) to determine the formula mass for each ionic compound.
- TiO2
- AgBr
- Au(NO3)3
- Fe3(PO4)2
Answer
a. 79.87 amu
b. 187.77 amu
c. 383.0 amu
Percent Composition of a Compound from a Chemical Formula
The percent composition of a compound can also be determined from the formula of the compound. The subscripts in the formula are first used to calculate the mass of each element in one mole of the compound. That is divided by the molar mass of the compound and multiplied by \(100\%\).
\[\% \: \text{by mass} = \frac{\text{mass of element in} \: 1 \: \text{mol}}{\text{molar mass of compound}} \times 100\% \nonumber \]
The percent composition of a given compound is always the same as long as the compound is pure.
Dichlorine heptoxide \(\left( \ce{Cl_2O_7} \right)\) is a highly reactive compound used in some organic synthesis reactions. Calculate the percent composition of dichlorine heptoxide.
Solution
| Steps for Problem Solving | Example |
|---|---|
| Identify the "given"information and what the problem is asking you to "find." |
Given : Cl2O7 Find: % Composition (% Cl and %O) |
| List other known quantities |
Mass of Cl in 1 mol Cl2O7 , 2 Cl : 2 x 35.45 g = 70.90 g Mass of O in 1 mol Cl2O7 , 7 O: 7 x 16.00 g = 112.00 g Molar mass of Cl2O7 = 182.90 g/mol |
| Cancel units and calculate. |
\[\% \ce{Cl} = \frac{70.90 \: \text{g} \: \ce{Cl}}{182.90 \: \text{g}} \times 100\% = 38.76\% \: \ce{Cl} \nonumber \] \[\% \: \ce{O} = \frac{112.00 \: \text{g} \: \ce{O}}{182.90 \: \text{g}} \times 100\% = 61.24\% \: \ce{O} \nonumber \] Calculate the percent by mass of each element by dividing the mass of that element in 1 mole of the compound by the molar mass of the compound and multiplying by \(100\%\). |
| Think about your result. | The percentages add up to \(100\%\). |
Percent composition can also be used to determine the mass of a certain element that is contained in any mass of a compound. In the previous sample problem, it was found that the percent composition of dichlorine heptoxide is \(38.76\% \: \ce{Cl}\) and \(61.24\% \: \ce{O}\). Suppose that you needed to know the masses of chlorine and oxygen present in a \(12.50 \: \text{g}\) sample of dichlorine heptoxide. You can set up a conversion factor based on the percent by mass of each element.
\[12.50 \: \text{g} \: \ce{Cl_2O_7} \times \frac{38.76 \: \text{g} \: \ce{Cl}}{100 \: \text{g} \: \ce{Cl_2O_7}} = 4.845 \: \text{g} \: \ce{Cl} \nonumber \]
\[12.50 \: \text{g} \: \ce{Cl_2O_7} \times \frac{61.24 \: \text{g} \: \ce{O}}{100 \: \text{g} \: \ce{Cl_2O_7}} = 7.655 \: \text{g} \: \ce{O} \nonumber \]
The sum of the two masses is \(12.50 \: \text{g}\), the mass of the sample size.
Barium fluoride is a transparent crystal that can be found in nature as the mineral frankdicksonite. Determine the percent composition of barium fluoride.
- Answer a:
- 78.32% Ba and 21.67% F
Summary
- The mole (symbol: mol) is the base unit of amount of substance ("number of substance") in the International System of Units or System International (SI), defined as exactly 6.02214076×1023 particles, e.g., atoms, molecules, ions or electrons.
- Avogadro's number is related to moles of any substance X as follows:
\[\text{1 mol X} = 6.022 \times 10^{23} \text{ X atoms}. \nonumber \]
- Formula masses of ionic and molecular compounds can be determined from the masses of the atoms in their formulas.
- Processes are described for calculating the percent composition of a compound based on the chemical formula.
Contributors and Attributions
Anonymous
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook
Henry Agnew (UC Davis)
- Wikipedia

