5.2: Volume Relationships in Chemical Equations
- Page ID
- 152162
- Identify the relative volume of gas consumed or produced based on a balanced chemical equation for a reaction.
The behavior of gases can be represented by gas laws as will be discussed in more detail in Chapter 6. Avogadro's law states that all gases (that show ideal behavior) contain the same number of molecules in the same volume (at the same temperature and pressure). Thus, the ratios of volumes of gases involved in a chemical reaction are given by the coefficients in the equation for the reaction, provided that the gas volumes are measured at the same temperature and pressure.
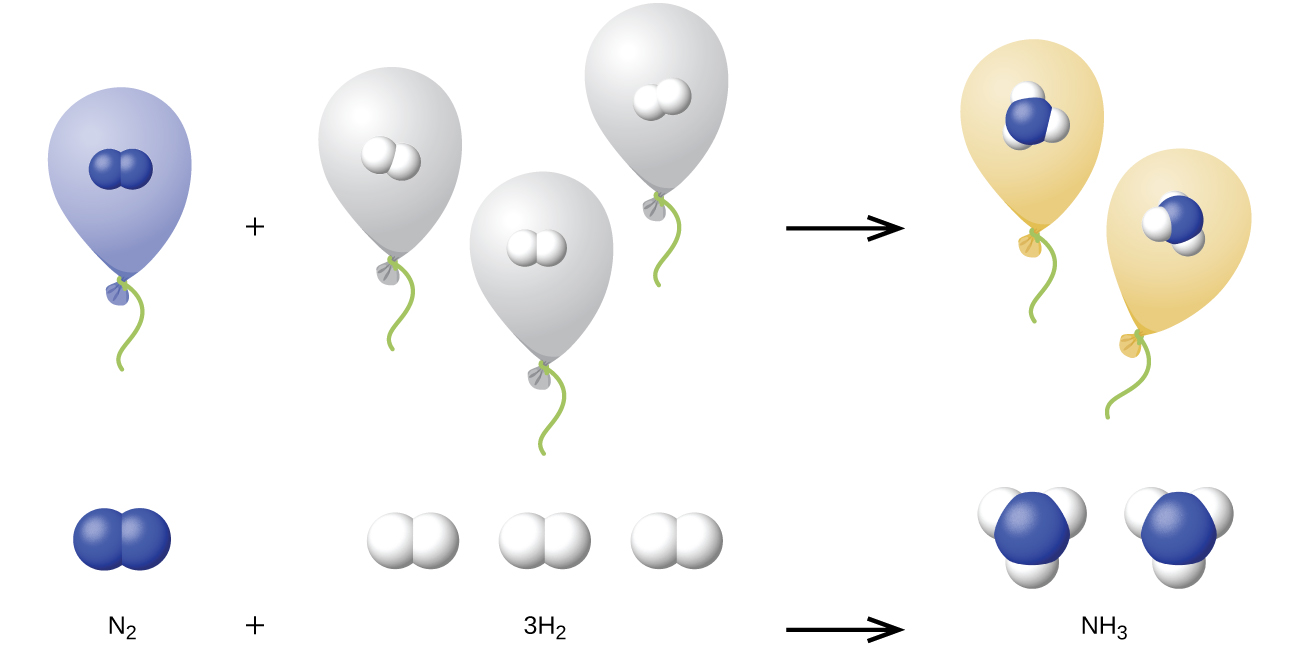
We can extend Avogadro’s law (that the volume of a gas is directly proportional to the number of moles of the gas) to chemical reactions with gases: Gases combine, or react, in definite and simple proportions by volume, provided that all gas volumes are measured at the same temperature and pressure. For example, since nitrogen and hydrogen gases react to produce ammonia gas according to the balanced equation below
\[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
a given volume of nitrogen gas reacts with three times that volume of hydrogen gas to produce two times that volume of ammonia gas, if pressure and temperature remain constant.
The explanation for this is illustrated in Figure \(\PageIndex{1}\). According to Avogadro’s law, equal volumes of gaseous N2, H2, and NH3, at the same temperature and pressure, contain the same number of molecules. Because one molecule of N2 reacts with three molecules of H2 to produce two molecules of NH3, the volume of H2 required is three times the volume of N2, and the volume of NH3 produced is two times the volume of N2.
Propane, C3H8(g), is used in gas grills to provide the heat for cooking. What volume of O2(g) measured at 25 °C and 760 torr is required to react with 2.7 L of propane measured under the same conditions of temperature and pressure? Assume that the propane undergoes complete combustion.
Solution
The ratio of the volumes of C3H8 and O2 will be equal to the ratio of their coefficients in the balanced equation for the reaction:
&\ce{C3H8}(g)+\ce{5O2}(g) ⟶ &&\ce{3CO2}(g)+\ce{4H2O}(l)\\
\ce{&1\: volume + 5\: volumes &&3\: volumes + 4\: volumes}
\end{align} \nonumber \]
From the equation, we see that one volume of C3H8 will react with five volumes of O2:
A volume of 13.5 L of O2 will be required to react with 2.7 L of C3H8.
An acetylene tank for an oxyacetylene welding torch provides 9340 L of acetylene gas, C2H2, at 0 °C and 1 atm. How many tanks of oxygen, each providing 7.00 × 103 L of O2 at 0 °C and 1 atm, will be required to burn the acetylene?
\[\ce{2C2H2 + 5O2⟶4CO2 + 2H2O} \nonumber \]
- Answer
-
3.34 tanks (2.34 × 104 L)
Ammonia is an important fertilizer and industrial chemical. Suppose that a volume of 683 billion cubic feet of gaseous ammonia, measured at 25 °C and 1 atm, was manufactured. What volume of H2(g), measured under the same conditions, was required to prepare this amount of ammonia by reaction with N2?
Solution
Because equal volumes of H2 and NH3 contain equal numbers of molecules and each three molecules of H2 that react produce two molecules of NH3, the ratio of the volumes of H2 and NH3 will be equal to 3:2. Two volumes of NH3, in this case in units of billion ft3, will be formed from three volumes of H2:
The manufacture of 683 billion ft3 of NH3 required 1020 billion ft3 of H2. (At 25 °C and 1 atm, this is the volume of a cube with an edge length of approximately 1.9 miles.)
What volume of O2(g) measured at 25 °C and 760 torr is required to react with 17.0 L of ethylene, C2H4(g), measured under the same conditions of temperature and pressure? The products are CO2 and water vapor.
- Answer
-
51.0 L
Summary
Avogadro's law may be used to determine the volume of gaseous reactant(s) or product(s) based on a balanced chemical equation.
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

