12.7: Limiting Reactant
- Page ID
- 53795
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Don't you hate running out of cooking ingredients?
Cooking is a great example of everyday chemistry. In order to correctly follow a recipe, a cook needs to make sure that he has plenty of all the necessary ingredients in order to make his dish. Let us suppose that you are deciding to make some pancakes for a large group of people. The recipe on the box indicates that the following ingredients are needed for each batch of pancakes:
\(1\) cup of pancake mix
\(\frac{3}{4}\) cup milk
\(1\) egg
\(1\) tablespoon vegetable oil
Now you check the pantry and the refrigerator and see that you have the following ingredients available:
2 boxes of pancake mix (8 cups)
Half a gallon of milk (4 cups)
2 eggs
Full bottle of vegetable oil (about 3 cups)
The question that you must ask is: how many batches of pancakes can I make? The answer is two. Even though you have enough pancake mix, milk, and oil to make many more batches of pancakes, you are limited by the fact that you only have two eggs. As soon as you have made two batches of pancakes, you will be out of eggs and your "reaction" will be complete.
Limiting Reactant
For a chemist, the balanced chemical equation is the recipe that must be followed. As you have seen earlier, the Haber process is a reaction in which nitrogen gas is combined with hydrogen gas to form ammonia. The balanced equation is shown below.
\[\ce{N_2} \left( g \right) + 3 \ce{H_2} \left( g \right) \rightarrow 2 \ce{NH_3} \left( g \right)\nonumber \]
We know that the coefficients of the balanced equation indicate the mole ratio that is required for this reaction to occur. One mole of \(\ce{N_2}\) will react with three moles of \(\ce{H_2}\) to form two moles of \(\ce{NH_3}\).
Now let us suppose that a chemist were to react three moles of \(\ce{N_2}\) with six moles of \(\ce{H_2}\) (see figure below).
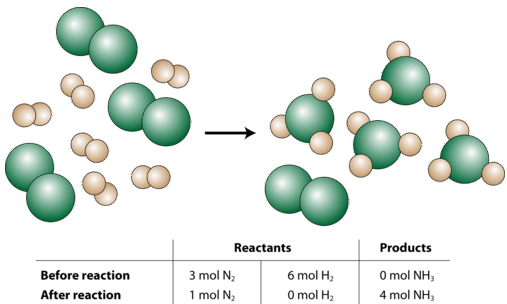
So what happened in this reaction? The chemist started with 3 moles of \(\ce{N_2}\). You may think of this as being 3 times as much as the "recipe" (the balanced equation) requires since the coefficient for the \(\ce{N_2}\) is a 1. However, the 6 moles of \(\ce{H_2}\) that the chemist started with is only two times as much as the "recipe" requires, since the coefficient for the \(\ce{H_2}\) is a 3 and \(3 \times 2 = 6\). So, after the reaction is complete, the hydrogen gas will be completely used up; while there will be 1 mole of nitrogen gas left over. Finally, the reaction will produce 4 moles of \(\ce{NH_3}\) because that is also two times as much as shown in the balanced equation. The overall reaction that occurred in words:
\[2 \: \text{mol} \: \ce{N_2} + 6 \: \text{mol} \: \ce{H_2} \rightarrow 4 \: \text{mol} \: \ce{NH_3}\nonumber \]
All the amounts are doubled from the original balanced equation.
The limiting reactant (or limiting reagent) is the reactant that determines the amount of product that can be formed in a chemical reaction. The reaction proceeds until the limiting reactant is completely used up. In our example above, the \(\ce{H_2}\) is the limiting reactant. The excess reactant (or excess reagent) is the reactant that is initially present in a greater amount than will eventually be reacted. In other words, there is always excess reactant left over after the reaction is complete. In the above example, the \(\ce{N_2}\) is the excess reactant.
Summary
- The amount of limiting reactant determines how much product will be formed in a chemical reaction.
Review
- In the Haber reaction illustrated above, how do we know that hydrogen is the limiting reactant?
- What if hydrogen were left over?
- Which material would be limiting if no hydrogen or nitrogen were left over?