2.E: Measurements (Exercises)
- Page ID
- 64977
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercises (Expressing Numbers)
1. Express these numbers in scientific notation.
- 56.9
- 563,100
- 0.0804
- 0.00000667
2. Express these numbers in scientific notation.
- −890,000
- 602,000,000,000
- 0.0000004099
- 0.000000000000011
3. Express these numbers in scientific notation.
- 0.00656
- 65,600
- 4,567,000
- 0.000005507
4. Express these numbers in scientific notation.
- 65
- −321.09
- 0.000077099
- 0.000000000218
5. Express these numbers in standard notation.
- 1.381 × 105
- 5.22 × 10−7
- 9.998 × 104
6. Express these numbers in standard notation.
- 7.11 × 10−2
- 9.18 × 102
- 3.09 × 10−10
7. Express these numbers in standard notation.
- 8.09 × 100
- 3.088 × 10−5
- −4.239 × 102
8. Express these numbers in standard notation.
- 2.87 × 10−8
- 1.78 × 1011
- 1.381 × 10−23
9. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.
- 72.44 × 103
- 9,943 × 10−5
- 588,399 × 102
10. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.
- 0.000077 × 10−7
- 0.000111 × 108
- 602,000 × 1018
11. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.
- 345.1 × 102
- 0.234 × 10−3
- 1,800 × 10−2
12. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.
- 8,099 × 10−8
- 34.5 × 100
- 0.000332 × 104
13. Write these numbers in scientific notation by counting the number of places the decimal point is moved.
- 123,456.78
- 98,490
- 0.000000445
14. Write these numbers in scientific notation by counting the number of places the decimal point is moved.
- 0.000552
- 1,987
- 0.00000000887
15. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.
- 456 × (7.4 × 108) = ?
- (3.02 × 105) ÷ (9.04 × 1015) = ?
- 0.0044 × 0.000833 = ?
16. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.
- 98,000 × 23,000 = ?
- 98,000 ÷ 23,000 = ?
- (4.6 × 10−5) × (2.09 × 103) = ?
17. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.
- 45 × 132 ÷ 882 = ?
- [(6.37 × 104) × (8.44 × 10−4)] ÷ (3.2209 × 1015) = ?
18. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.
- (9.09 × 108) ÷ [(6.33 × 109) × (4.066 × 10−7)] = ?
- 9,345 × 34.866 ÷ 0.00665 = ?
Answers
-
- 5.69 × 101
- 5.631 × 105
- 8.04 × 10−2
- 6.67 × 10−6
-
- 6.56 × 10−3
- 6.56 × 104
- 4.567 × 106
- 5.507 × 10−6
-
- 138,100
- 0.000000522
- 99,980
-
- 8.09
- 0.00003088
- −423.9
-
- 7.244 × 104
- 9.943 × 10−2
- 5.88399 × 107
-
- 3.451 × 104
- 2.34 × 10−4
- 1.8 × 101
-
- 1.2345678 × 105
- 9.849 × 104
- 4.45 × 10−7
-
- 3.3744 × 1011
- 3.3407 × 10−11
- 3.665 × 10−6
-
- 6.7346 × 100
- 1.6691 × 10−14
Exercises (Expressing Units)
1. Identify the unit in each quantity.
- 2 boxes of crayons
- 3.5 grams of gold
2. Identify the unit in each quantity.
- 32 oz of cheddar cheese
- 0.045 cm3 of water
3. Identify the unit in each quantity.
- 9.58 s (the current world record in the 100 m dash)
- 6.14 m (the current world record in the pole vault)
4. Identify the unit in each quantity.
- 2 dozen eggs
- 2.4 km/s (the escape velocity of the moon, which is the velocity you need at the surface to escape the moon's gravity)
5. Indicate what multiplier each prefix represents.
- k
- m
- M
6. Indicate what multiplier each prefix represents.
- c
- G
- μ
7. Give the prefix that represents each multiplier.
- 1/1,000th ×
- 1,000 ×
- 1,000,000,000 ×
8. Give the prefix that represents each multiplier.
- 1/1,000,000,000th ×
- 1/100th ×
- 1,000,000 ×
9. Complete the following table with the missing information.
| Unit | Abbreviation |
|---|---|
| kilosecond | |
| mL | |
| Mg | |
| centimeter |
10. Complete the following table with the missing information.
| Unit | Abbreviation |
|---|---|
| kilometer per second | |
| second | |
| cm3 | |
| μL | |
| nanosecond |
11. Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 3.44 × 10−6 s
- 3,500 L
- 0.045 m
12. Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 0.000066 m/s (Hint: you need consider only the unit in the numerator.)
- 4.66 × 106 s
- 7,654 L
13. Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 43,600 mL
- 0.0000044 m
- 1,438 ms
14. Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 0.000000345 m3
- 47,000,000 mm3
- 0.00665 L
15. Multiplicative prefixes are used for other units as well, such as computer memory. The basic unit of computer memory is the byte (b). What is the unit for one million bytes?
16. You may have heard the terms microscale or nanoscale to represent the sizes of small objects. What units of length do you think are useful at these scales? What fractions of the fundamental unit of length are these units?
17. Acceleration is defined as a change in velocity per time. Propose a unit for acceleration in terms of the fundamental SI units.
18. Density is defined as the mass of an object divided by its volume. Propose a unit of density in terms of the fundamental SI units.
Answers
- boxes of crayons
- grams of gold
3.
- seconds
- meters
5.
- 1,000 x
- 1/1,000 x
- 1,000,000 x
7.
- milli-
- kilo-
- giga-
9.
|
Unit |
Abbreviation |
|---|---|
|
kilosecond |
ks |
|
milliliter |
mL |
|
megagram |
Mg |
|
centimeter |
cm |
- 3.44 μs
- 3.5 kL
- 4.5 cm
13.
- 43.6 mL
- 4.4 μm
- 1.438 s
15. megabytes (Mb)
17. meters/second2
Exercises (Significant Figures)
1. Express each measurement to the correct number of significant figures.

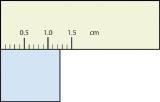
2. Express each measurement to the correct number of significant figures.


3. How many significant figures do these numbers have?
- 23
- 23.0
- 0.00023
- 0.0002302
4. How many significant figures do these numbers have?
- 5.44 × 108
- 1.008 × 10−5
- 43.09
- 0.0000001381
5. How many significant figures do these numbers have?
- 765,890
- 765,890.0
- 1.2000 × 105
- 0.0005060
6. How many significant figures do these numbers have?
- 0.009
- 0.0000009
- 65,444
- 65,040
7. Compute and express each answer with the proper number of significant figures, rounding as necessary.
- 56.0 + 3.44 = ?
- 0.00665 + 1.004 = ?
- 45.99 − 32.8 = ?
- 45.99 − 32.8 + 75.02 = ?
8. Compute and express each answer with the proper number of significant figures, rounding as necessary.
- 1.005 + 17.88 = ?
- 56,700 − 324 = ?
- 405,007 − 123.3 = ?
- 55.5 + 66.66 − 77.777 = ?
9. Compute and express each answer with the proper number of significant figures, rounding as necessary.
- 56.7 × 66.99 = ?
- 1.0÷ 77 = ?
- 1.00÷ 77.0 = ?
- 6.022 × 1.89 = ?
10. Compute and express each answer with the proper number of significant figures, rounding as necessary.
- 0.000440 × 17.22 = ?
- 203,000 ÷ 0.044 = ?
- 67 × 85.0 × 0.0028 = ?
- 999,999 ÷ 3,310 = ?
11. a. Write the number 87,449 in scientific notation with four significant figures.
b. Write the number 0.000066600 in scientific notation with five significant figures.
12. a. Write the number 306,000,000 in scientific notation to the proper number of significant figures.
b. Write the number 0.0000558 in scientific notation with two significant figures
13. Perform each calculation and limit each answer to three significant figures.
- 67,883 × 0.004321 = ?
- (9.67 × 103) × 0.0055087 = ?
14. Perform each calculation and limit each answer to four significant figures.
- 18,900 × 76.33 ÷ 0.00336 = ?
- 0.77604 ÷ 76,003 × 8.888 = ?
Answers
1.
- 375 psi
- 1.30 cm
3.
- two
- three
- two
- four
5.
- five
- seven
- five
- four
7.
- 59.4
- 1.011
- 13.2
- 88.2
9.
- 3.80 × 103
- 0.013
- 0.0130
- 11.4
11. a. \(8.745 \times 10^4\)
b. \(6.6600 \times 10^{-5}\)
13. a. 293
b. 53.3
Exercises (Converting Units)
1. Write the two conversion factors that exist between the two given units.
- milliliters and liters
- microseconds and seconds
- kilometers and meters
2. Write the two conversion factors that exist between the two given units.
- kilograms and grams
- milliseconds and seconds
- centimeters and meters
3. Perform the following conversions.
- 5.4 km to meters
- 0.665 m to millimeters
- 0.665 m to kilometers
4. Perform the following conversions.
- 90.6 mL to liters
- 0.00066 ML to liters
- 750 L to kiloliters
5. Perform the following conversions.
- 17.8 μg to grams
- 7.22 × 102 kg to grams
- 0.00118 g to nanograms
6. Perform the following conversions.
- 833 ns to seconds
- 5.809 s to milliseconds
- 2.77 × 106 s to megaseconds
7. Perform the following conversions.
- 9.44 m2 to square centimeters
- 3.44 × 108 mm3 to cubic meters
8. Perform the following conversions.
- 0.00444 cm3 to cubic meters
- 8.11 × 102 m2 to square nanometers
9. Why would it be inappropriate to convert square centimeters to cubic meters?
10. Why would it be inappropriate to convert from cubic meters to cubic seconds?
11. Perform the following conversions.
- 45.0 m/min to meters/second
- 0.000444 m/s to micrometers/second
- 60.0 km/h to kilometers/second
12. Perform the following conversions.
- 3.4 × 102 cm/s to centimeters/minute
- 26.6 mm/s to millimeters/hour
- 13.7 kg/L to kilograms/milliliters
13. Perform the following conversions.
- 0.674 kL to milliliters
- 2.81 × 1012 mm to kilometers
- 94.5 kg to milligrams
14. Perform the following conversions.
- 6.79 × 10−6 kg to micrograms
- 1.22 mL to kiloliters
- 9.508 × 10−9 ks to milliseconds
15. Perform the following conversions.
- 6.77 × 1014 ms to kiloseconds
- 34,550,000 cm to kilometers
16. Perform the following conversions.
- 4.701 × 1015 mL to kiloliters
- 8.022 × 10−11 ks to microseconds
17. Perform the following conversions. Note that you will have to convert units in both the numerator and the denominator.
- 88 ft/s to miles/hour (Hint: use 5,280 ft = 1 mi.)
- 0.00667 km/h to meters/second
18. Perform the following conversions. Note that you will have to convert units in both the numerator and the denominator.
- 3.88 × 102 mm/s to kilometers/hour
- 1.004 kg/L to grams/milliliter
19. What is the area in square millimeters of a rectangle whose sides are 2.44 cm × 6.077 cm? Express the answer to the proper number of significant figures.
20. What is the volume in cubic centimeters of a cube with sides of 0.774 m? Express the answer to the proper number of significant figures.
21. The formula for the area of a triangle is 1/2 × base × height. What is the area of a triangle in square centimeters if its base is 1.007 m and its height is 0.665 m? Express the answer to the proper number of significant figures.
22. The formula for the area of a triangle is 1/2 × base × height. What is the area of a triangle in square meters if its base is 166 mm and its height is 930.0 mm? Express the answer to the proper number of significant figures.
Answers
1.
- \(\dfrac{1000mL}{1L} \;and\; \dfrac{1L}{1000mL}\nonumber \)
- \(\dfrac{1000000\mu s}{1s}\;and\; \dfrac{1s}{1000000\mu s}\nonumber \)
- \(\dfrac{1000m}{1km}\;and\; \dfrac{1km}{1000m}\nonumber \)
3.
- 5,400 m
- 665 mm
- 6.65 × 10−4 km
5.
- 1.78 × 10−5 g
- 7.22 × 105 g
- 1.18 × 106 ng
7.
- 94,400 cm2
- 0.344 m3
9. One is a unit of area, and the other is a unit of volume.
11.
- 0.75 m/s
- 444 µm/s
- 1.666 × 10−2 km/s
13.
- 674,000 mL
- 2.81 × 106 km
- 9.45 × 107 mg
15.
- 6.77 × 108 ks
- 345.5 km
17.
- 6.0 × 101 mi/h
- 0.00185 m/s
19. 1.48 × 103 mm2
21. 3.35 × 103 cm2
Exercises (Other Units - Temperature and Density)
1. Perform the following conversions.
- 255°F to degrees Celsius
- −255°F to degrees Celsius
- 50.0°C to degrees Fahrenheit
- −50.0°C to degrees Fahrenheit
2. Perform the following conversions.
- 1,065°C to degrees Fahrenheit
- −222°C to degrees Fahrenheit
- 400.0°F to degrees Celsius
- 200.0°F to degrees Celsius
3. Perform the following conversions.
- 100.0°C to kelvins
- −100.0°C to kelvins
- 100 K to degrees Celsius
- 300 K to degrees Celsius
4. Perform the following conversions.
- 1,000.0 K to degrees Celsius
- 50.0 K to degrees Celsius
- 37.0°C to kelvins
- −37.0°C to kelvins
- Convert 0 K to degrees Celsius. What is the significance of the temperature in degrees Celsius?
- Convert 0 K to degrees Fahrenheit. What is the significance of the temperature in degrees Fahrenheit?
- The hottest temperature ever recorded on the surface of the earth was 136°F in Libya in 1922. What is the temperature in degrees Celsius and in kelvins?
- The coldest temperature ever recorded on the surface of the earth was −128.6°F in Vostok, Antarctica, in 1983. What is the temperature in degrees Celsius and in kelvins?
- Give at least three possible units for density.
- What are the units when density is inverted? Give three examples.
- A sample of iron has a volume of 48.2 cm3. What is its mass?
- A sample of air has a volume of 1,015 mL. What is its mass?
- The volume of hydrogen used by the Hindenburg, the German airship that exploded in New Jersey in 1937, was 2.000 × 108 L. If hydrogen gas has a density of 0.0899 g/L, what mass of hydrogen was used by the airship?
- The volume of an Olympic-sized swimming pool is 2.50 × 109 cm3. If the pool is filled with alcohol (d = 0.789 g/cm3), what mass of alcohol is in the pool?
- A typical engagement ring has 0.77 cm3 of gold. What mass of gold is present?
- A typical mercury thermometer has 0.039 mL of mercury in it. What mass of mercury is in the thermometer?
- What is the volume of 100.0 g of lead if lead has a density of 11.34 g/cm3?
- What is the volume of 255.0 g of uranium if uranium has a density of 19.05 g/cm3?
- What is the volume in liters of 222 g of neon if neon has a density of 0.900 g/L?
- What is the volume in liters of 20.5 g of sulfur hexafluoride if sulfur hexafluoride has a density of 6.164 g/L?
- Which has the greater volume, 100.0 g of iron (d = 7.87 g/cm3) or 75.0 g of gold (d = 19.3 g/cm3)?
- Which has the greater volume, 100.0 g of hydrogen gas (d = 0.0000899 g/cm3) or 25.0 g of argon gas (d = 0.00178 g/cm3)?
Answers
1.
- 124°C
- −159°C
- 122°F
- −58°F
3.
- 373 K
- 173 K
- −173°C
- 27°C
5. −273°C. This is the lowest possible temperature in degrees Celsius.
7. 57.8°C; 331 K
9. g/mL, g/L, and kg/L (answers will vary)
11. 379 g
13. 1.80 × 107 g
15. 15 g
17. 8.818 cm3
19. 247 L
21. The 100.0 g of iron has the greater volume
Additional Exercises
- Evaluate 0.00000000552 × 0.0000000006188 and express the answer in scientific notation. You may have to rewrite the original numbers in scientific notation first.
-
Evaluate 333,999,500,000 ÷ 0.00000000003396 and express the answer in scientific notation. You may need to rewrite the original numbers in scientific notation first.
-
Express the number 6.022 × 1023 in standard notation.
-
Express the number 6.626 × 10−34 in standard notation.
-
When powers of 10 are multiplied together, the powers are added together. For example, 102 × 103 = 102+3 = 105. With this in mind, can you evaluate (4.506 × 104) × (1.003 × 102) without entering scientific notation into your calculator?
-
When powers of 10 are divided into each other, the bottom exponent is subtracted from the top exponent. For example, 105/103 = 105−3 = 102. With this in mind, can you evaluate (8.552 × 106) ÷ (3.129 × 103) without entering scientific notation into your calculator?
-
Consider the quantity two dozen eggs. Is the number in this quantity "two" or "two dozen"? Justify your choice.
-
Consider the quantity two dozen eggs. Is the unit in this quantity "eggs" or "dozen eggs"? Justify your choice.
-
Fill in the blank: 1 km = ______________ μm.
-
Fill in the blank: 1 Ms = ______________ ns.
-
Fill in the blank: 1 cL = ______________ ML.
-
Fill in the blank: 1 mg = ______________ kg.
-
Express 67.3 km/h in meters/second.
-
Express 0.00444 m/s in kilometers/hour.
-
Using the idea that 1.602 km = 1.000 mi, convert a speed of 60.0 mi/h into kilometers/hour.
-
Using the idea that 1.602 km = 1.000 mi, convert a speed of 60.0 km/h into miles/hour.
-
Convert 52.09 km/h into meters/second.
-
Convert 2.155 m/s into kilometers/hour.
-
Use the formulas for converting degrees Fahrenheit into degrees Celsius to determine the relative size of the Fahrenheit degree over the Celsius degree.
-
Use the formulas for converting degrees Celsius into kelvins to determine the relative size of the Celsius degree over kelvins.
-
What is the mass of 12.67 L of mercury?
-
What is the mass of 0.663 m3 of air?
-
What is the volume of 2.884 kg of gold?
-
What is the volume of 40.99 kg of cork? Assume a density of 0.22 g/cm3.
Answers
1. 3.42 × 10−18
3. 602,200,000,000,000,000,000,000
5. 4.520 × 106
7. The quantity is two; dozen is the unit.
9.1,000,000,000
11. 1/100,000,000
13. 18.7 m/s
15. 96.1 km/h
17. 14.47 m/s
19. One Fahrenheit degree is nine-fifths the size of a Celsius degree.
21. 1.72 × 105 g
23. 149 mL


