Coordination Numbers and Geometry
- Page ID
- 518
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The total number of points of attachment to the central element is termed the coordination number and this can vary from 2 to as many as 16, but is usually 6. In simple terms, the coordination number of a complex is influenced by the relative sizes of the metal ion and the ligands and by electronic factors, such as charge which is dependent on the electronic configuration of the metal ion.
Introduction
Based on the radius ratio, it can be seen that the bigger the charge on the central ion, the more attraction there will be for negatively charged ligands, however at the same time, the bigger the charge the smaller the ion becomes which then limits the number of groups able to coordinate. It is important to recognize that every geometry has a specific coordination number, but every complex wish a specific coordination number will have a choice of several possible geometries (i.e., there is not a one-to-one correspondance between coordination number and geometry).
Coordination Number 2
This arrangement is not very common for first row transition metal ion complexes and some of the best known examples are for Silver(I). In this case we have a low charge and an ion at the right hand side of the d-block indicating smaller size
Coordination Number 3
Once again, this is not very common for first row transition metal ions. Examples with three different geometries have been identified:
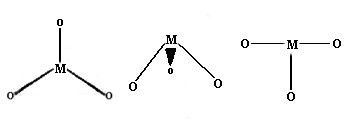
- Trigonal planar Geometry: Well known for main group species like CO32- etc., this geometry has the four atoms in a plane with the bond angles between the ligands at 120 degrees.
Figure 2: The Trigonal planar [Cu(CN)3]2- system
- Trigonal pyramid Geometry: More common with main group ions.
- T-shaped: The first example of a rare T-shaped molecule was found in 1977.
Coordination Number 4
Two different geometries are possible. The tetrahedron is the more common while the square planar is found almost exclusively with metal ions having a d8 electronic configuration.
- Tetrahedral Geometry: The chemistry of molecules centered around a tetrahedral C atom is covered in organic courses. To be politically correct, please change all occurrences of C to Co. There are large numbers of tetrahedral Cobalt(II) complexes known.
- Square Planar Geometry: This is fairly rare and is included only because some extremely important molecules exist with this shape.

Coordination Number 5
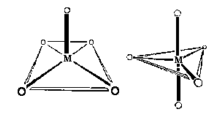
- Square pyramid Geometry: Oxovanadium salts (Vanadyl, VO2+) often show square pyramidal geometry, for example, VO(acac)2. Note that the Vanadium(IV) can be considered coordinatively unsaturated and addition of pyridine leads to the formation of an octahedral complex.
- Trigonal Bipyramid Geometry: The structure of [Cr(en)3][Ni(CN)5] 1.5 H2O was reported in 1968 to be a remarkable example of a complex exhibiting both types of geometry in the same crystal. The reaction of cyanide ion with Ni2+ proceeds via several steps:
\[ Ni^{2+} + 2 CN^- \rightarrow Ni(CN)_2 \nonumber \]
\[ Ni(CN)_2 + 2 CN^- \rightarrow \underset{\text{orange-red}}{[Ni(CN)_4]^{2-}} \nonumber \]
with \(\log(\beta_4) = 30.1\)
\[ [Ni(CN)_4]^{2-} + CN^- \rightarrow \underset{\text{deep red}}{[Ni(CN)_5]^{3-}} \nonumber \]

Coordination Number 6
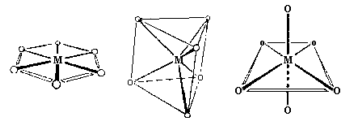
- Hexagonal planar Geometry: Unknown for first row transition metal ions, although the arrangement of six groups in a plane is found in some higher coordination number geometries.
- Trigonal prism Geometry: Most trigonal prismatic compounds have three bidentate ligands such as dithiolates or oxalates and few are known for first row transition metal ions.
- Octahedral (Oh): The most common geometry found for first row transition metal ions, including all aqua ions. In some cases distortions are observed and these can sometimes be explained in terms of the Jahn-Teller Theorem.
Coordination Number 7
Not very common for 1st row complexes and the energy difference between the structures seems small and distortions occur so that prediction of the closest "idealized" shape is generally difficult. Three geometries are possible:
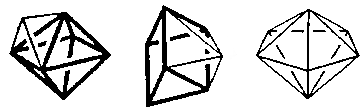
- Capped octahedron (C3v) Geometry
- Capped trigonal prism (C2v)
- Pentagonal Bipyramid (D5h)

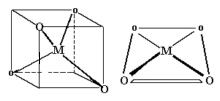
Coordination Number 8
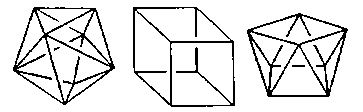
- Dodecahedron (D2d) Geometry
- Cube (Oh) Geometry
- Square antiprism (D4d) Geometry
- Hexagonal bipyramid (D6h) Geometry
Coordination Number 9
- Three-face centered trigonal prism (D3h) Geometry
Coordination Number 10
- Bicapped square antiprism (D4d) Geometry
Coordination Number 11
- All-faced capped trigonal prism (D3h) Geometry: This is not a common stereochemistry.
Figure 9: aqua-(12-crown-4)-tris(nitrato-O,O')-cerium(III) (12-crown-4) solvate and (15-crown-5)-tris(nitrato-O,O')-cerium(III) the Cerium ion is 11 coordinate.
Coordination Number 12
- cuboctahedron (Oh) Geometry

Contributors and Attributions
Prof. Robert J. Lancashire (The Department of Chemistry, University of the West Indies)

