Excess and Limiting Reagents
- Page ID
- 31600
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Stoichiometric mixture
- Excess reagent
- Limiting reagent
- Use stoichiometric calculation to determine excess and limiting reagents in a chemical reaction and explain why.
- Calculate theoretical yields of products formed in reactions that involve limiting reagents.
Chemical reaction equations give the ideal stoichiometric relationship among reactants and products. However, the reactants for a reaction in an experiment are not necessarily a stoichiometric mixture. In a chemical reaction, reactants that are not used up when the reaction is finished are called excess reagents. The reagent that is completely used up or reacted is called the limiting reagent, because its quantity limits the amount of products formed.
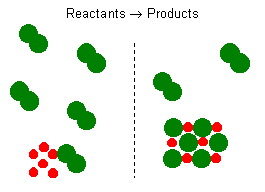
Let us consider the reaction between solid sodium and chlorine gas. The reaction can be represented by the equation:
\[\mathrm{2 Na_{\large{(s)}} + Cl_{2\large{(g)}} \rightarrow 2 NaCl_{\large{(s)}}} \nonumber \]
It represents a reaction of a metal and a diatomic gas chlorine. This balanced reaction equation indicates that two \(\ce{Na}\) atoms would react with two \(\ce{Cl}\) atoms or one \(\ce{Cl2}\) molecule. Thus, if you have 6 \(\ce{Na}\) atoms, 3 \(\ce{Cl2}\) molecules will be required. If there is an excess number of \(\ce{Cl2}\) molecules, they will remain unreacted. We can also state that 6 moles of sodium will require 3 moles of \(\ce{Cl2}\) gas. If there are more than 3 moles of \(\ce{Cl2}\) gas, some will remain as an excess reagent, and the sodium is a limiting reagent. It limits the amount of the product that can be formed.
Chemical reactions with stoichiometric amounts of reactants have no limiting or excess reagents.
Calculate the number of moles of \(\ce{CO2}\) formed in the combustion of ethane \(\ce{C2H6}\) in a process when 35.0 mol of \(\ce{O2}\) is consumed.
HINT
The reaction is
\[\ce{2 C2H6 + 7 O2 \rightarrow 4 CO2 + 6 H2O} \nonumber \]
\[\mathrm{35.0\: mol\: O_2 \times\dfrac{4\: mol\: CO_2}{7\: mol\: O_2} = 20.0\: mol\: CO_2} \nonumber \]
DISCUSSION
A balanced equation for the reaction is a basic requirement for identifying the limiting reagent even if amounts of reactants are known.
Two moles of \(\ce{Mg}\) and five moles of \(\ce{O2}\) are placed in a reaction vessel, and then the \(\ce{Mg}\) is ignited according to the reaction
\(\mathrm{Mg + O_2 \rightarrow MgO}\).
Identify the limiting reagent in this experiment.
HINT
Before a limiting reagent is identified, the reaction must be balanced. The balanced reaction is
\[\mathrm{2 Mg + O_2 \rightarrow 2 MgO} \nonumber \]
Thus, two moles of \(\ce{Mg}\) require only ONE mole of \(\ce{O2}\). Four moles of oxygen will remain unreacted. Therefore, oxygen is the excess reagent, and \(\ce{Mg}\) is the limiting reagent.
DISCUSSION
Answer these questions:
How many moles of \(\ce{MgO}\) is formed?
What is the weight of \(\ce{MgO}\) formed?
Skill Developing Problems
- At room temperature (25 °C) what is the state of sodium: solid, gas or liquid?
Hint: Sodium metal
- Equal weights of \(\ce{H2}\) and \(\ce{O2}\) are placed in a balloon and then ignited. Assuming reaction goes to completion, which gas is the excess reagent?
Hint: hydrogen
Hint: Iron oxide
Discussion -
A stoichiometric mixture has a mass ratio of 54:160 (nearly 1:3) for \(\ce{Al:Fe2O3}\).
Contributors and Attributions
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)

