4.12: The trans/cis Effects and Influences
- Page ID
- 707
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The trans effect is an ancient but venerable observation. First noted by Chernyaev in 1926, the trans effect and its conceptual siblings (the trans influence, cis influence, and cis effect) are easy enough to comprehend. That is, it’s simple enough to know what they are. To understand why they are, on the other hand, is much more difficult.
Definitions & Examples
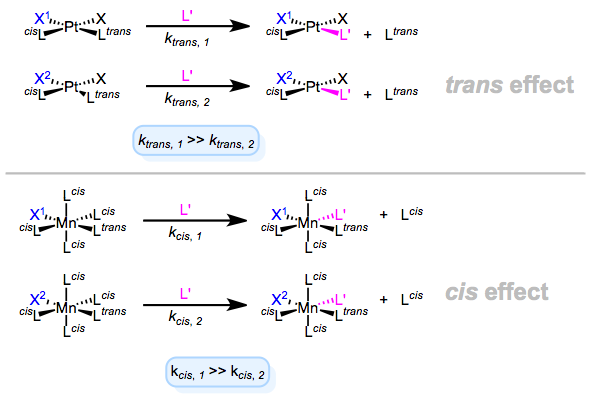
Let’s begin with definitions: what is the trans effect? There’s some confusion on this point, so we need to be careful. The trans effect proper, which is often called the kinetic trans effect, refers to the observation that certain ligands increase the rate of ligand substitution when positioned trans to the departing ligand. The key word in that last sentence is “rate”—the trans effect proper is a kinetic effect. The trans influence refers to the impact of a ligand on the length of the bond trans to it in the ground state of a complex. The key phrase there is “ground state”—this is a thermodynamic effect, so it’s sometimes called the thermodynamic trans effect. Adding to the insanity, cis effects and cis influences have also been observed. Evidently, ligands may also influence the kinetics or thermodynamics of their cis neighbors. All of these phenomena are independent of the metal center, but do depend profoundly on the geometry of the metal (more on that shortly).
Kinetic trans and cis effects are shown in the figure below. In both cases, we see that X1 exhibits a stronger effect than X2. The geometries shown are those for which each effect is most commonly observed. The metals and oxidation states shown are prototypical.
On to the influences, which are simpler to illustrate since they’re concerned with ground states, not reactions. The lengthened bonds below are exaggerated.
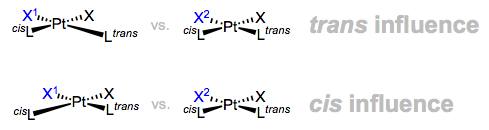
And there we have it folks, the thermodynamic and kinetic cis/trans effects. It’s worth keeping in mind that the kinetic trans effect is most common for d8 square planar complexes, and the kinetic cis effect is most common for d6 octahedral complexes (particularly when the departing L is CO). But a lingering question remains: what makes for a strong trans effect ligand?
Origins of Effects & Influences
The trans effect and its cousins are all electronic, not steric effects. So, the electronic properties of the ligand dictate the strength of its trans effect. Let’s finally dig into the trans effect series:
(weak) F–, HO–, H2O <NH3 < py < Cl– < Br– < I–, SCN–, NO2–, SC(NH2)2, Ph– < SO32– < PR3 < AsR3, SR2, H3C– < H–, NO, CO, NC–, C2H4 (strong)
What’s the electronic progression here? It’s clear that electronegativity decreases across the series: F– < Cl– < Br– < I– < H3C–. From a bonding perspective, we can say that ligands with strong trans effects are strong σ-donors (or σ-bases). Yet σ-donation doesn’t tell the whole story. What about ethylene and carbon monoxide, which both appear at the top of the heap? Neither of these ligands are strong σ-donors, but their π systems do interact with the metal center through backbonding. Consider the following sub-series: S=C=N– < PR3 < CO. Backbonding increases across this series, along with the strength of the trans effect. Strong backbonders—better known as π-acceptors or π-acids—exhibit strong trans effects.
Strong trans effect = strong σ-donor + strong π-acceptor
Wonderful! Using these ideas we can identify ligands with strong trans effects. But we can dive deeper down the rabbit hole: why does this particular combination of electronic factors lead to a strong trans effect? To understand this, we need to know the mechanism of the ligand substitution reaction that’s sped up by strong trans effect ligands. For 16-electron Pt(II) complexes, associative substitution is par for the course. The incoming ligand binds to the metal first, forming an 18-electron complex (yay!), which jettisons a ligand to yield a new 16-electron product. The mechanism in all its glory is shown in the figure below.
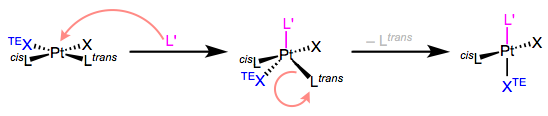
Some very important points about this mechanism:
- The incoming ligand always sits at an equatorial site in the trigonal bipyramidal intermediate. More on this another day, but I think of this result as governed by the principle of least motion. Consider the molecular gymnastics that would have to happen to place the incoming ligand in an axial position.
- Two ligands in the square plane are “pushed down” and become the other two equatorial ligands.
- Owing to microscopic reversibility, the leaving group must be one of the equatorial ligands.
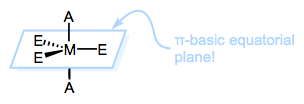
The third point reveals that once L’ has “pushed down” XTE and Ltrans, Ltrans has no choice but to leave (assuming XTE stays put). Thus, the trans effect has nothing to do with the second step of the mechanism, which is not rate determining anyway. The key is the first step—in particular, the “pushing down” event. Apparently, ligands with strong trans effects like to be pushed down. They like to occupy the equatorial plane of the TBP intermediate. Now here’s the kicker: the equatorial sites of the TBP geometry are more π basic than the axial sites. The equatorial plane is just the xy-plane of the metal center, and the d orbitals in that plane (when occupied) are great electron sources for π-acidic ligands. Thus, π-acidic ligands want to occupy those equatorial sites, to receive the benefits of strong backbonding! Boom; strong π-acids encourage loss of the ligand trans to themselves.
What about those pesky σ donors? Well, we can imagine that in a square planar complex, a ligand and its trans partner are competing for donation into the same d orbital. Strong σ donation from a ligand should thus weaken the bond trans to it. Although this is the thermodynamic trans effect (trans influence) in action, the resulting destabilization of the ground state relative to the transition state is a kinetic effect. On the whole, the barrier to substitution of the trans ligand goes down as σ-donating strength goes up.
This idea of “competition for the metal center” is a nice heuristic to use when thinking about the trans and cis influences. The type of metallic orbital involved in M–L bonding determines the strength of L’s trans and cis influences on neighboring ligands that also need that metallic orbital for bonding. For example: both influences are large if the metal’s s orbital is a significant contributor to M–L bonding, since it’s non-directional; the trans influence is much greater than the cis influence when metallic p orbitals are primarily involved in M–L. For a deeper explanation of these ideas, see this paper.
Summing up
Perhaps the most valuable lesson from a study of the trans effect is that many concepts from organometallic chemistry involve more than meets the eye. Geometric effects and influences are real icebergs, in the sense that the observations and trends are easy to grasp, but difficult to explain. We had to dig all the way into the mechanism of associative ligand substitution before a satisfactory explanation emerged!


