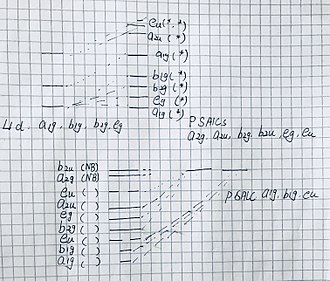1.10: D4h Molecular Orbitals
- Page ID
- 204711
The D4h point group are one of the most common molecular symmetry found in nature. For example, the XeF4 molecule belongs to the D4h point group. the XeF4 contains one C4 rotation axis, one C2 rotation axis, and four C2 perpendicular rotation axis, 2σv planes, 2σd planes and 1σh plane, those composed the character table of the D4h Point group.
| E | 2C4 | C2 | 2C'2 | 2C"2 | i | 2S4 | σh | 2σv | 2σd | Linear's Rotation | Quadractic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1g | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x2+y2, z2 | |
| A2g | 1 | 1 | 1 | -1 | -1 | 1 | 1 | 1 | -1 | -1 | Rz | x2-y2 |
| B1g | 1 | -1 | 1 | 1 | -1 | 1 | -1 | 1 | 1 | -1 | xy | |
| B2g | 1 | -1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | 1 | (xz, yz) | |
| Eg | 2 | 0 | -2 | 0 | 0 | 2 | 0 | -2 | 0 | 0 | (Rx, Ry) | |
| A1u | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | ||
| A2u | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | z | |
| B1u | 1 | -1 | 1 | 1 | -1 | -1 | 1 | -1 | -1 | 1 | ||
| B2u | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | ||
| Eu | 2 | 0 | -2 | 0 | 0 | -2 | 0 | 2 | 0 | 0 | (x, y) | |
| σ | 4 | 0 | 0 | 2 | 0 | 0 | 0 | 4 | 2 | 0 | ||
| \(\pi\) | 8 | 0 | 0 | -4 | 0 | 0 | 0 | 0 | 0 | 0 |
To compose a Molecular Diagram of a molecule with D4h symmetry group, we should first find the irreducible representation of the ligands and of the center molecule. and then find the SALCS for each of the irreducible representation and finally, compose the molecular diagram. To take an easy example, the Square Planar Complexes.. starting with the sigma orbital of the ligands, the reducible representation of the sigma orbital is the total number of atoms that do not move under each operation. For the Pi orbital, we have to degenerate the pi orbital has two degrees of freedom, thus, the reducible representation of the pi orbital can also be found by using the similar method. and then, by using the projection operation method, we can find the irreducible representations of the ligand's sigma and pi orbital. In this case, the sigma orbital has A1g, B1g, Eu three irreducible representations and the pi orbital has A2g, A2u, B2g, B2u, Eg and Eu.
| E | 2C4 | C2 | 2C’2 | 2C’’2 | i | 2S4 | σh | 2σv | 2σd | |
|---|---|---|---|---|---|---|---|---|---|---|
| sigma | 4 | 0 | 0 | 2 | 0 | 0 | 0 | 4 | 2 | 0 |
| Pi | 8 | 0 | 0 | -4 | 0 | 0 | 0 | 0 | 0 | 0 |
Move on the central atom, we can find irreducible representation of the valence orbitals on the central atoms by using the character table. The results are as follow:
| Representation | Orbital |
|---|---|
| A1g | s, dz2 |
| B1g | dx2- y2 |
| B2g | dxy |
| Eg | dxz, dyz |
| A2u | Pz |
| Eu | Px, py |