4.3.2: Representations of Point Groups
- Page ID
- 226817
Symmetry Operations: Matrix Representations
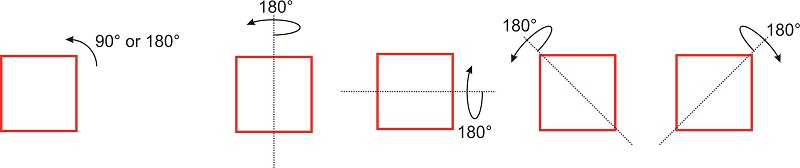
A symmetry operation, such as a rotation around a symmetry axis or a reflection through a plane, is an operation that, when performed on an object, results in a new orientation of the object that is indistinguishable from the original. For example, if we rotate a square in the plane by \(\pi/2\) or \(\pi\), the new orientation of the square is superimposable on the original one (Figure \(\PageIndex{1}\)).
If rotation by an angle \(\theta\) of a molecule (or object) about some axis results in an orientation of the molecule (or object) that is superimposable on the original, the axis is called a rotation axis. The molecule (or object) is said to have an \(n\)-fold rotational axis, where \(n\) is \(2\pi/\theta\). The axis is denoted as \(C_n\). The square of Figure \(\PageIndex{1}\) has a \(C_4\) axis perpendicular to the plane because a \(90^{\circ}\) rotation leaves the figure indistinguishable from the initial orientation. This axis is also a \(C_2\) axis because a \(180^{\circ}\) degree rotation leaves the square indistinguishable from the original square. In addition, the figure has several other \(C_2\) axis that lie on the same plane as the square:
A symmetry operation moves all the points of the object from one initial position to a final position, and that means that symmetry operators are \(3\times 3\) square matrices (or \(2\times 2\) in two dimensions). Each symmetry operation can be expressed as a transformation matrix where the vector \((x',y',z')\) represents the new coordinates of the point \((x,y,z)\) after the symmetry operation.
\[[\text{New Coordinates} (x',y',z')] = [\text{Transformation Matrix}] \times [\text{Old Coordinates} (x,y,z)] \nonumber \]
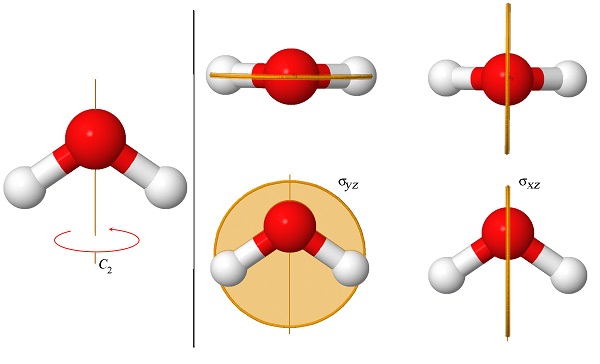
We will use the example of water, which is in the \(C_{2v}\) point group, to illustrate how transformation matrices can be used to represent the symmetry of a group.
Figure \(\PageIndex{2}\) shows the three symmetry elements of the molecule of water (H\(_2\)O). This molecule has only one rotation axis, which is 2-fold, and therefore we call it a “\(C_2\) axis.” It also has two mirror planes, one that contains the two hydrogen atoms (\(\sigma_{yz}\)), and another one perpendicular to it (\(\sigma_{xz}\)). Both planes contain the C\(_2\) axis.
Transformation Matrix of \(C_2\) rotation
A 2-fold rotation around the \(z-\)axis changes the location of a point \((x,y,z)\) to \((-x,-y,z)\) (see Figure \(\PageIndex{3}\)). By convention, rotations are always taken in the counterclockwise direction.
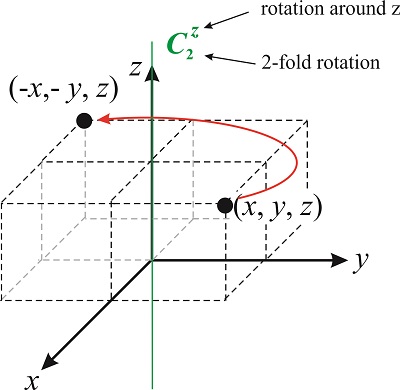
What is the matrix that represents the \(C_2\) rotation? The matrix transforms the vector \((x,y,z)\) into \((-x,-y,z)\), so
\[{C_2}(x,y,z)=(-x,-y,z) \nonumber \]
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} -x \\ -y \\ z \end{pmatrix} \nonumber \]
We know the matrix is a \(3\times 3\) square matrix because it needs to multiply a 3-dimensional vector. In addition, we write the vector as a vertical column to satisfy the requirements of matrix multiplication.
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix} \nonumber \]
\[a_{11}x+a_{12}y+a_{13}z=-x \nonumber \]
\[a_{21}x+a_{22}y+a_{23}z=-y \nonumber \]
\[a_{31}x+a_{32}y+a_{33}z=z \nonumber \]
and we conclude that \(a_{11}=-1\), \(a_{12}=a_{13}=0\), \(a_{22}=-1\), \(a_{21}=a_{23}=0\) and \(a_{33}=1\), \(a_{31}=a_{32}=0\). The transformation matrix of the \(C_2\) operation of the \(C_{2v}\) point group is:
\[C_2=\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]
Transformation Matrix of \(\sigma_{xz}\) reflection
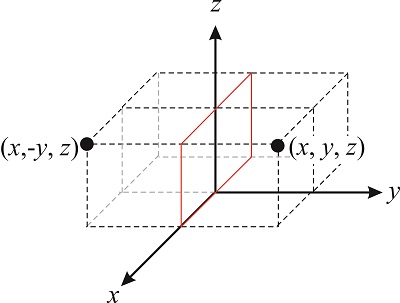
Rotations are not the only symmetry operations we can perform on a molecule. Figure \(\PageIndex{4}\) illustrates the reflection of a point through the \(xz\) plane. This operation transforms the vector \((x,y,z)\) into the vector \((x,-y,z)\). Symmetry operators involving reflections through a plane are usually denoted with the letter \(\sigma\), so the operator that reflects a point through the \(xz\) plane is \(\hat{\sigma}_{xz}\):
\[\sigma_{xz}(x,y,z)=(x,-y,z) \nonumber \]
Following the same logic we used for the rotation matrix, we can write the \(\sigma_{xz}\) transformation matrix as:
\[\sigma_{x,z}=\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]
This is true because
\[\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} x \\ -y \\ z \end{pmatrix} \nonumber \]
Find the transformation matrix of the identity (E) and the \(\sigma_{y,z}\) operations under the \(C_{2v}\) point group.
- Answer
-
The transformation matrix for \(E\) is \(\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\).
The transformation matrix for \(\sigma_{v(yz)"}\) is \(\begin{pmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\).
Characters
For a square matrix, the character is the trace of the matrix. For the \(C_2\) operation, with the transformation matrix
\[\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}, \nonumber \]
the trace is \((-1) + (-1) + 1 = -1\).
The set of characters for a point group is called a reducible representation (\(\Gamma\)). The reducible representation for the \(C_{2v}\) point group is:
\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]
Prove that the characters in the reducible representation for \(C_{2v}\) are correct:
\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]
- Answer
-
For the \(E\) operation, with the transformation matrix \(\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), the trace is \(1 + 1 + 1 = \) \(3\).
For the \(C^z_2\) operation, with the transformation matrix \(\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), the trace is \((-1) + (-1) + 1 =\) \( -1\).
For the \(\sigma_{v(xz)'}\) operation, with the transformation matrix \(\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), the trace is \(1 + (-1) + 1 =\) \(1\).
For the \(\sigma_{v(yz)"}\) operation, with the transformation matrix \(\begin{pmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), the trace is \(-1 + 1 + 1 =\) \(1\).
This gives the reducible representation \(\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \)
Reducible and Irreducible Representations
Let us now go back and look in more detail at the transformation matrices of the \(C_{2v}\) point group that we derived above. If we look at the matrices carefully we see that they all take the same block diagonal form (a square matrix is said to be block diagonal if all the elements are zero except for a set of submatrices lying along the diagonal).
\[E=\begin{pmatrix} {\color{red}[1]}&0&0 \\ 0&{\color{blue}[1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix}, \, C_2=\begin{pmatrix} {\color{red}[-1]}&0&0 \\ 0&{\color{blue}[-1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} ,\, \sigma_{v(xz)}'=\begin{pmatrix} {\color{red}[1]}&0&0 \\ 0&{\color{blue}[-1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} ,\, \sigma_{v(yz)"}=\begin{pmatrix} \color{red}[-1]&0&0 \\ 0&{\color{blue}[1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} \nonumber \]
All the non-zero elements become 1x1 matrices that each represent individual \({\color{red}x}, {\color{blue}y}, {\color{green}z}\) coordinates. In other words, the element \(\color{red}a_{11}\) represents \(\color{red}x\), \(\color{blue}a_{22}\) represents \(\color{blue}y\), and \(\color{green}a_{33}\) represents \(\color{green}z\). The matrix elements for x from each transformation matrix combine to form an irreducible representation of the \(C_{2v}\) point group. Likewise, the matrix elements for y combine to form a second irreducible representation, and the same is true for z elements. These irreducible representations are shown below:
\[\begin{array}{l|llll|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & \text{Coordinate Used}\\ \hline & \color{red}1 & \color{red}-1&\color{red}1&\color{red}-1 & \color{red}x \\ & \color{blue}1 & \color{blue}-1 & \color{blue}-1 & \color{blue}1 & \color{blue}y \\ & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}z\\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]
The irreducible representations add to form the reducible representation, \(\Gamma\). This \(\Gamma\), which is the set of 3x3 matrices, can be reduced to the set of 1x1 matrices of the irreducible representations. The irreducible representations cannot be reduced further, hence their name.
Sources & Attribution
- Parts of this page was adapted from Matrices (click here) (Symmetry Operators), contributed by Marcia Levitus, Associate Professor (Biodesign Institute) at Arizona State University.
- Parts of this page were adapted from Reductions of Representations, contributed by
Claire Vallance (University of Oxford)
Curated or created by Kathryn Haas


