3.2: Symmetry Operations and Elements
- Page ID
- 2596
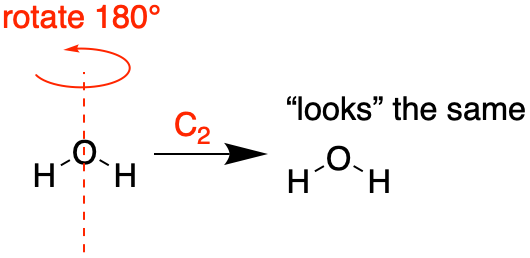
Figure \(\PageIndex{1}\): An example of a symmetry operation is a 180° rotation where the resulting position is indistinguishable from the original. A 180° rotation is called a C2 operation; the axis of rotation is the symmetry element. (CC-BY-NC-SA; Kathryn Haas) |
Introduction
The symmetry of a molecule consists of symmetry operations and symmetry elements. A symmetry operation is an operation that is performed to a molecule which leaves it indistinguishable and superimposable on the original position. Symmetry operations are performed with respect to symmetry elements (points, lines, or planes).
An example of a symmetry operation is a 180° rotation of a water molecule in which the resulting position of the molecule is indistinguishable from the original position (see Figure \(\PageIndex{1}\)). In this example, the symmetry operation is the rotation and the symmetry element is the axis of rotation.
There are five types of symmetry operations including identity, reflection, inversion, proper rotation, and improper rotation. The improper rotation is the sum of a rotation followed by a reflection. The symmetry elements that correspond to the five types of symmetry operations are listed in Table \(\PageIndex{1}\).
| Element | Operation | Symbol |
|---|---|---|
| Identity | identity | E |
| Proper axis | rotation by (360/n)o | Cn |
| Symmetry plane | reflection in the plane | σ |
| Inversion center | inversion of a point at (x,y,z) to (-x,-y,-z) | i |
| Improper axis | rotation by (360/n)o, followed by reflection in the plane perpendicular to the rotation axis | Sn |
Symmetry Operations and Elements
Identity (E)
All molecules have the identity element. The identity operation is doing nothing to the molecule (it doesn't rotate, reflect, or invert...it just is).
Proper Rotation and Proper Axis (Cn)
A "proper" rotation is just a simple rotation operation about an axis. The symbol for any proper rotation or proper axis is C(360/n), where n is the degree of rotation. Thus, a 180° rotation is a C2 rotation around a C2 axis, and a 120° rotation is a C3 rotation about a C3 axis.
PRINCIPLE AXIS: The principle axis of a molecule is the highest order proper rotation axis. For example, if a molecule had C2 and C4 axes, the C4 is the principle axis.
Reflection and Symmetry Planes (σ)
Symmetry planes are mirror planes within the molecule. A reflection operation occurs with respect to a plane of symmetry. There are three classes of symmetry elements:
- σh (horizontal): horizontal planes are perpendicular to principal axis
- σv (vertical): vertical planes are parallel to the principal axis
- σd (dihedral): dihedral planes are parallel to the principle axis and bisecting two C2' axes
Inversion and Inversion Center (i)
The inversion operation requires a point of symmetry (a center of symmetry within a molecule). In other words, a point at the center of the molecule that can transform (x,y,z) into (-x,-y,-z) coordinate. Structures of tetrahedron, triangles, and pentagons lack an inversion center.
Improper rotation (Sn)
Improper rotation is a combination of a rotation with respect to an axis of rotation (Cn), followed by a reflection through a plane perpendicular to that Cn axis. In short, and Sn operation is equivalent to Cn followed by \(\sigma_h\).
References
- Introduction to Molecular Symmetry by J. S Ogden
- Inorganic Chemistry by Catherine Housecroft And Alan G. Sharpe.
Problems
1. Water molecule H2O was used as an example and was mentioned that water was rotated 180 degree around an axis bisecting the oxygen, then the molecule was superimposable on the original water molecule, how about CO2? Is it going to be like the water molecule since CO2 also has 2 atoms of oxygen.
Of course not, because every molecule has different molecular shape. To recognize the symmetry of any molecule the structure and the molecular shape of that molecule should be defined. The water molecule is bent but CO2 is not, and if CO2 is rotated 360 degree around the axis bisecting the C atom then it can be superimposed on the original molecule. We then see the symmetry for the CO2.
2. Why should all of the five symmetry elements be done on a molecule in order to find the point group the molecule belongs to, why is performing only one or two of the symmetry elements not enough for recognizing the point group?
One or two of the symmetry elements will not be able to tell us everything about the molecule's symmetry since those one or two properties do not tell us everything about the molecule. Also, while different molecules may have one or two symmetrical properties in common, the five properties will not be the same for all molecules.
3. What does the symbol Cn stand for and what does n represent? Why is it important to identify n?
C is the axis of rotation and n is the order of the axis.
4. How are the character tables helpful?
The character table tells us about all the operational elements performed on the molecule and indicates if we have forgotten to perform any of the symmetry elements. The tables serve as a checklist because all the operational elements should be done on the molecule in order to find the point group of the molecule.
5. Why is important to find symmetry in molecules?
Symmetry tells us about bounding for that molecular bonding.

