15.2: The Isolobal Analogy
- Page ID
- 151451
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The isolobal analogy (aka isolobal principle) is a strategy used in organometallic chemistry to relate the structure of organic and inorganic molecular fragments in order to predict bonding properties of organometallic compounds. Roald Hoffmann described molecular fragments as isolobal: "if the number, symmetry properties, approximate energy and shape of the frontier orbitals and the number of electrons in them are similar – not identical, but similar." One can predict the bonding and reactivity of a species from that of a better-understood species if the two molecular fragments have similar frontier orbitals; the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Isolobal compounds are analogues to isoelectronic compounds that share the same number of valence electrons and structure.
Isolobal species are indicated with an isolobal arrow symbol; a double-headed arrow with half an orbital (Figure \(\PageIndex{1}\)).

The concept of isolobality was developed by Roald Hoffmann (Figure \(\PageIndex{2}\)), who won the Nobel prize in chemistry in 1981. It comes from the greek words “isos” meaning “similar” and “lobos” meaning lobe. Hence, “isolobal” means “similar lobes”. In his Nobel speech he defined isolobality as follows: “Molecular fragments are isolobal if the number, symmetry properties, approximate energy and shape of the frontier orbitals and the number of electrons in them are similar - not identical, but similar. “ When molecular fragments are isolobal then they can likely be combined to form a stable molecule. Thus, isolobal fragments are compatible building blocks for the construction of stable molecules. We can also say that the concept of isolobality helps us to predict when a stable bond forms. Whenever two molecular fragments are isolobal, then they will likely form stable bonds between them.

Isolobal Fragments of main group elements
There is a simple means to determine if fragments are isolobal. In main group chemistry the octet rule is a very helpful guide, especially for the period 2 elements (B,C,N,O,F) for which the octet rule holds fairly strictly. The difference between the number "8" and the number of valence electrons (VE) of the molecular fragment is equal to the number of frontier orbitals and the number of electrons in it.
# of frontier orbitals = # of electrons in frontier orbitals = 8 – VE
Thus, when two fragments (of main group elements) have the same number of valence electrons, they can be considered isolobal. For example, the \(\ce{CH3}\) fragment created by homolytic cleavage of a \(\ce{C-H}\) bond from \(\ce{CH4}\) is shown in Figure \(\PageIndex{1}\). This \(\ce{CH3}\) fragment has 7 VE on the carbon, and therefore it has one frontier orbital with one electron it (Figure \(\PageIndex{1}\)). The same is true for the \(\ce{NH2}\) (7 VE) and \(\ce{OH}\) (7 VE) fragments shown in XXX. All of these fragments have 7 VE and one frontier orbital (Figure \(\PageIndex{3}\)).

According to the isolobal analogy, it should be possible to combine isolobal fragments to form stable molecules. Let's test this on the fragments shown in Figure \(\PageIndex{3}\). All the posible combinations are shown in Figure \(\PageIndex{4}\). Two \(\ce{CH3}\) fragments can be combined to form an ethane molecule which is known to be stable. The combination of \(\ce{CH3}\) and\(\ce{NH2}\) gives methylamine which is stable, and the combination of \(\ce{CH3}\) and \(\ce{OH}\) gives methanol, which is also stable. Two\(\ce{NH2}\) fragments give hydrazine, H2N-NH2 which exists, the combination of\(\ce{NH2}\)and \(\ce{OH}\) gives the known hydroxylamine molecule \(\ce{NH2OH}\). The combination of two \(\ce{OH}\) fragments gives hydrogen peroxide \(\ce{H2O2}\).

As another example, a \(\ce{CH2}\) fragment is a 6 VE fragment, thus there are 8-6=2 frontier orbitals with overall two electrons in them (Figure \(\PageIndex{5}\)). An \(\ce{NH}\)-fragment and an O-atom also have 6 VE, and are therefore isolobal to \(\ce{CH2}\). In \(\ce{NH}\) there are 5+1=6 valence electrons, and an oxygen atom has 6 valence electrons. We can combine two \(\ce{CH2}\) fragments to form ethene \(\ce{H2C=CH2}\). Combining \(\ce{CH2}\) with \(\ce{NH}\) and \(\ce{O}\), respectively gives methanimine \(\ce{H2CNH}\), and formaldehyde \(\ce{H2C=O}\), respectively. Methylene imine is stable in the gas phase, and oligomerizes in higher concentrations to form a hexamer, called urotropine. Other oligomers and polymers are also known. The combination of two \(\ce{NH}\) fragments gives the known molecule diazene \(\ce{HN=NH}\), and the combination with an \(\ce{O}\) atom gives \(\ce{HN=O}\), which is known as nitroxyl or azanone, and is stable in the gas phase. The combination of two oxygen atoms gives the well known O2 molecule.
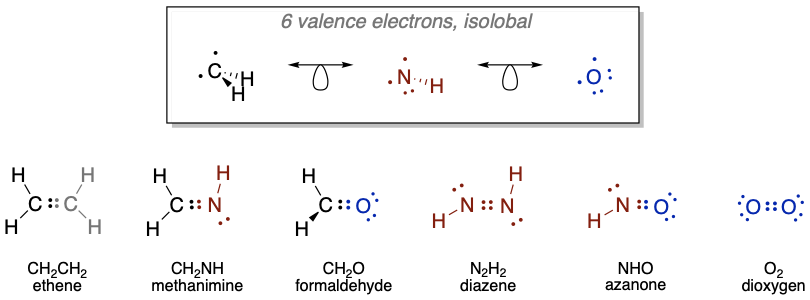
The analogy could also be extended to 5 VE fragments (not shown). The CH fragment has 4+1=5 VE, and an N-atom has 5 VE as well, thus they can be considered isolobal. Two CH fragments give acetylene C2H2, and two N atoms give the dinitrogen molecule N2. The combination of a CH fragment with an N fragment gives H-CN, well known as hydrogen cyanide.
Isolobal fragments of transition elements
In the way the octet rule can help to predict the number of frontier orbitals and the electrons in them for main group element fragments, the 18 electron rule can be used to predict the number of frontier orbitals and electrons for organometallic fragments, including carbonyl fragments. The number of frontier orbitals and the number of electrons in them is 18 minus the number of valence electrons the organometallic fragment has:
# frontier orbitals = # of electrons in frontier orbitals = 18 – VE
For example, a metal complex with a count of 17 electrons, such as \(\ce{Mn(CO)5}\), there is one frontier orbital with one electron. This implies that a 17 VE carbonyl fragment is isolobal to a 7 VE organic fragment such as \(\ce{CH3}\). For a 16 VE fragment such as \(\ce{Fe(CO)4}\) there are two frontier orbitals with one electron in each of them, and for a 15 VE fragment such as \(\ce{(CO)3Co}\) there are three frontier orbitals with overall three valence electrons (Figure \(\PageIndex{6}\)). Similarly, a 16 VE metal carbonyl fragment is isolobal to a 6 VE fragment such as \(\ce{CH2}\), and a 15 VE fragment is isolobal to a 5 VE fragment such as CH (Figure \(\PageIndex{6}\)).

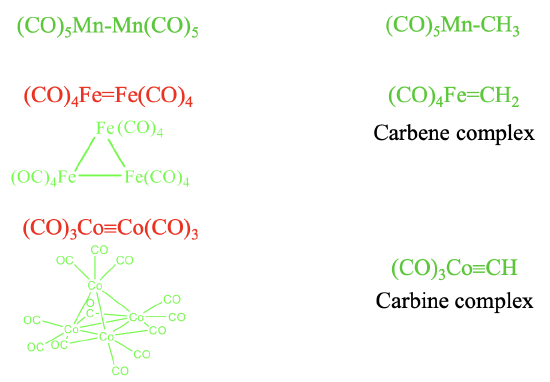
It should be possible to combine the isolobal fragments from Figure \(\PageIndex{6}\) to form stable molecules. Let us check how well this works (Figure \(\PageIndex{7}\)). It should be possible to combine the two 17 VE electron fragments such as \(\ce{Mn(CO)5}\) to form \(\ce{(CO)5Mn-Mn(CO)5}\). This is a known molecule. Remember we encountered it previously when we discussed the homoleptic carbonyls of metals with an odd number of electrons. Combining this fragment with a 7 VE \(\ce{CH3}\) fragment leads to \(\ce{(CO)5Mn-CH3}\) which is also stable.
Can we also combine two 16 VE electron fragments to form \(\ce{(CO)4Fe=Fe(CO)4}\) with an Fe=Fe double bond? The answer is no. Metal-metal double bonds, and also metal-metal triple bonds in carbonyl complexes are not formed. Instead clusters with single bonds are realized. The number of single bonds a metal makes is equal to the number of its frontier orbitals. In the case of 16 VE fragments trimeric clusters with single bonds are formed. In this cluster the two frontier orbitals of each fragment make two single bonds to two other fragments. In contrast, a 16 VE carbonyl fragment such as \(\ce{(CO)4Fe}\) can be combined with a 6 VE fragment to form a compound with a Fe=C double bond. A compound with a metal-carbon double bond is called a carbene complex. Similarly, the combination of 15 VE fragments of the type \(\ce{Co(CO)3}\) does not lead to a stable \(\ce{(CO)3Co≡Co(CO)3}\) molecule with a \(\ce{Co≡Co}\) triple bond. Instead, nature realizes a tetrameric tetrahedral cluster in which the three frontier orbitals of each 15 VE fragment make three single bonds to the other three 15 VE fragments. In clusters the CO ligands may not only be terminal, they can also be bridging. In the tetrameric Co-cluster, there are are nine terminal and three bridging CO-ligands. The three bridging CO ligands are connecting the three Co atoms at the base triangular face of the tetrahedron. What about the combination of a 15 VE fragment with an organic 5 VE fragment? The combination of a 15 VE fragment such as Co(CO)3 with a 5 VE organic fragment such as CH to does yield stable complexes such as the \(\ce{(CO)3Co≡CH}\) complex with a \(\ce{Co≡C}\) triple bond. Complexes with metal-carbon triple bonds are called carbine complexes.
Synthesis of Terameric Cluster Carbonyls
How can we make a carbonyl cluster like ((Co(CO)3)4?
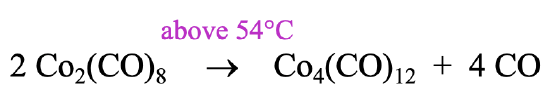
It can be prepared by heating the Co2(CO)8 to a temperature above 54°C. Above this temperature the reactant loses four CO ligands and rearranges to form the cluster (Fig. \(\PageIndex{8}\)). Interestingly, the higher homologues of the Co-cluster, the Rh4(CO)12 and the Ir4(CO)12 form spontaneously from the elements. Remember, that we previously determined that the Rh2(CO)8 and the Ir2(CO)8 are not stable. Rh and Ir favor the tetrameric clusters with 12 COs over the dimer with 8 CO ligands.
Structures of Co4(CO)12, Rh4(CO)12 and Ir4(CO)12
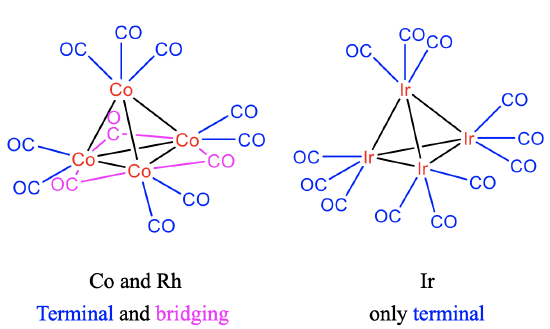
Like in the Co-cluster, there are 9 terminal and three bridging CO ligands in the Rh4(CO)12 cluster. By contrast, there are only terminal CO ligands in the iridium cluster (Fig.\(\PageIndex{9}\)) . This may be explained by the larger Ir-Ir bond length in comparison to the Co-Co and Rh-Rh bond lengths. The observation reflects the general rule that only 3d and 4d elements have bridging CO ligands, while only terminal ligands are observed in metals with 5d electrons.
Isoelectronic Charged Carbonyl Clusters
The previously discussed clusters were charge-neutral. Can we construct charged isoelectronic ones with different metals, and what is their stability? Let us start with the tetrameric Co-cluster made of four 15 VE fragments. The element left to the Co is the Fe. It has one electron less, therefore Fe(CO)3- is the 15 VE electron fragment which is isoelectronic to the neutral Co(CO)3 fragment. Its tetramer would be a Fe4(CO)124- cluster. This cluster is not known. The cluster already carries a 4- charge which is too high to support stable Fe-Fe bonds. Each Fe carries formally a 1- negative charge and there is too much electrostatic repulsion between the Fe atoms. Another possibility to realize a 15 VE fragment with Fe is a (CO)4Fe+ fragment. Here an additional ligand is added contributing two electrons, and one electron is removed resulting in a fragment with a 1+ charge. The fragment could be combined to form an Fe4(CO)164+ cluster. However, such a cluster is also not stable. This is because the coordination number would be 7, which is too high for a carbonyl. In addition, there is the destabilizing effect of the positive charge on the Fe-C bond. Similarly, tetramers of the 15 VE fragments Mn(CO)4, Cr(CO)4- and (CO)5Cr+ are also not known. Also in these cases, the coordination numbers would be too high. The Mn(CO)4 and the Cr(CO)4- would lead to a coordination number of 7, in the case of the Cr(CO)5+ fragment the coordination number would be even 8. We see here the limitations of the concept of isolobality. The presence of isolobality is not always sufficient to make a stable molecule, also other factors like coordination numbers and charge needs to be considered.What about charged isoelectronic clusters made from 16 VE? We saw previously that the neutral 16 VE Fe(CO)4 fragment gave a Fe3(CO)12 trimer. If we go from the Fe to the Mn, the isoelectronic 16 VE fragment would be a Mn(CO)4- fragment because Mn has one electron less than Fe. This fragment can indeed be trimerized to give a stable Mn3(CO)123- cluster with a 3- charge. This charge is not too high yet to destabilize the Mn-Mn bond and the coordination number of 6 is ideal for the stability of carbonyls. We could add a ligand and remove two electrons to produce a 15 VE Mn(CO)5+ fragment. However, in this case the coordination number would become 7 upon trimerization, which is too high to produce a stable cluster. In addition, the positive charge destabilizes the Mn-C bond. Replacing Mn by Cr in Mn(CO)5+ would give a neutral 16 VE Cr(CO)5 fragment, but its trimer is not stable because also in this case the coordination number becomes too high. Replacing Fe in Fe(CO)4 by Co would require a 1+ charge giving a Co(CO)4+ 16 VE fragment. Its trimer would have the coordination number 6, but it would carry a 4+ charge which is too high. A Co(CO)3- fragment would also have 16 VE, but its trimer is also not known, possibly because the relatively small coordination number of 5, which is less favorable than a coordination number of 6. Overall we can say as a rule for the stability for carbonyl clusters that there should not be positive charges, and no high negative charges. There should not be high coordination numbers.
Clusters with 16 VE and 6 VE Fragments

The cluster chemistry of carbonyls is even more versatile due to the possibility to substitute 16 and 15 VE fragments by 6 and 5 VE fragments, respectively. For instance, we can replace one 16 VE Fe(CO)4 fragment by a 6 VE CH2 fragment in the trimeric triiron dodecacarbonyl Fe3(CO)12 cluster (Fig. \(\PageIndex{10}\)). In the resulting cluster a methylene group bridges two Fe atoms, therefore the complex can be regarded a μ-methylene complex. The substitution reduces the number of cluster valence electrons (CVE) from 48 to 38. A second substitution of another 16 VE tetracarbonyl iron fragment by another 6 VE methylene fragment gives a cluster with two Fe-C bonds and one carbon-carbon bond having 28 cluster valence electrons. This complex can be regarded as a ethene complex in which an ethene molecule binds side-on to a 15 VE Fe(CO)4 fragment. Upon binding, the two Fe-C bonds are formed at the expense of the C-C π-bond and the bond order in the C-C bond is reduced from 2 to 1. If we substitute the last tetracarbonyl iron fragment by a third CH2 unit, then a completely organic molecule, cyclopropane, results. All the molecules are known to be stable molecules, and their stability can be nicely understood by using the concept of isolobality.
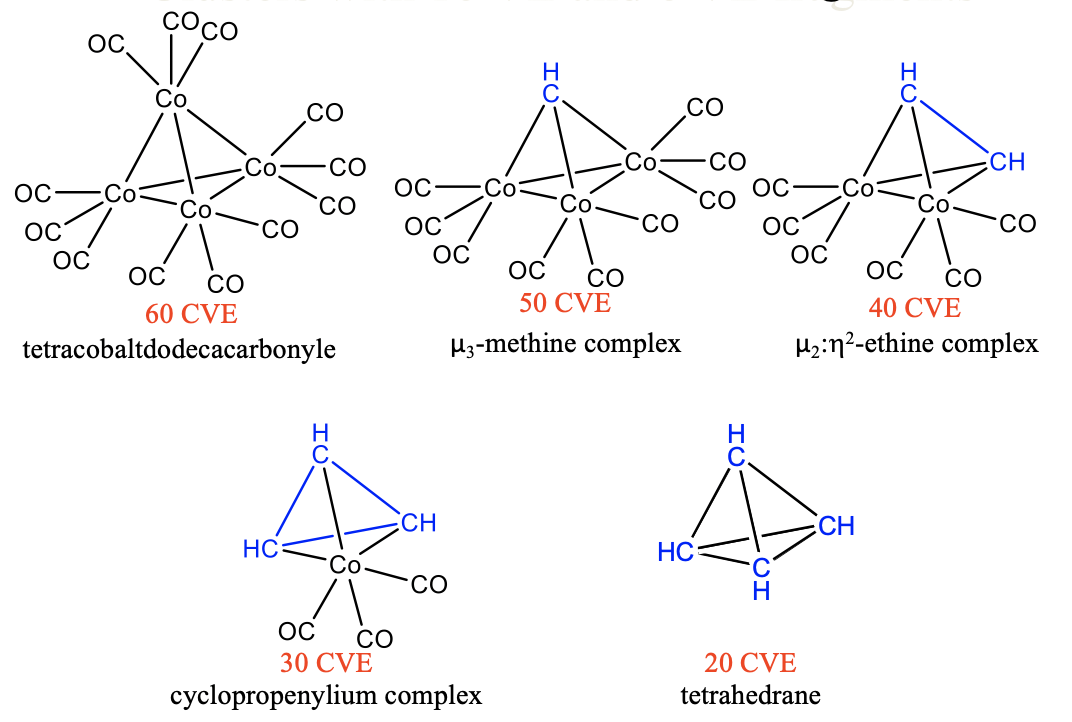
Similarly, we can substitute 15 VE tricarbonyl cobalt units by 5 VE CH fragments in tetracobaltdodecacarbonyl Co4(CO)12. A first substitution gives a 50 VE cluster with one CH fragment that makes three bonds to three Co(CO)4 fragments (Fig. \(\PageIndex{11}\)). Because the CH group bridges three metal atoms it is regarded a μ3-methine complex. A second substitution produces a 40 VE cluster with an organic CH-CH unit that makes four bonds to two Co atoms of two 15 VE Co(CO)3 fragments. The CH-CH fragment can be considered an ethine molecule binding side-on to a dicobalthexacarbonyl fragment, whereby the two π-bonds in ethine are expended to form four Co-C single bonds. The cluster can be considered a μ2:ƞ2-ethine complex because the ethine bridges two Co atoms and both carbons are involved in the bonding with Co. A third substitution leads to a 30 CVE cluster with three CH units binding to one Co(CO)3 fragment. There are three C-C single bonds and three Co-C bonds in the cluster. The three CH units form a cyclopropenylium complex that binds side-on to a Co(CO)4 fragment. A free cyclopropenylium molecule is a 3-ring with three π-electrons that are delocalized in the ring. Therefore, the bond order in a free cyclopropenylium molecule is 1.5. In the complex the three π-electrons are being used to make the three single bonds with the cobalt atoms. The bond order in cyclopropenylium is thereby reduced from 1.5 to 1. Finally, the fourth substitution of a tricarbonyl cobalt fragment by a methine fragment yields the completely organic tetrahedrane molecule. This molecule and the others discussed before are stable. The isolobality concept lets us rationalize these complex structures easily and understand their stability.
Synthesis of Cluster Complexes From Alkynes
The view that the 40 VE clusters are alkyne clusters is not just a formal view. They can be synthesized from alkynes. For instance alkyne-dicobalt clusters are accessible from dicobalt octacarbonyl and alkynes (Fig. \(\PageIndex{12}\)).
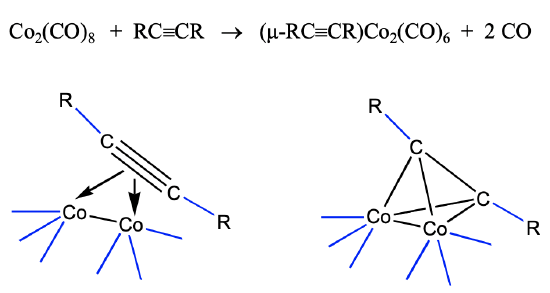
The cluster forms via the donation of the four π electrons of the alkynes into the metal d-orbitals of the dimeric cobalt carbonyl. This leads to a loss of of two CO ligands, and the formation of four Co-C bonds. Under harsher conditions the C-C triple bond can also cleave and this can give access to methine complexes.
Carbonyl Hydrides
Now let us leave the carbonyl cluster compounds and talk about another interesting class of carbonyls: carbonyl hydrides. They can be rationalized by the concept of isolobality as well. A hydrogen atom can be conceived as a species with one frontier orbital containing one electron. In this case the frontier orbital is simply the 1s orbital of the hydrogen. Thus, it should be possible to combine an H atom with a 17 VE carbonyl fragment like tetracarbonyl cobalt.
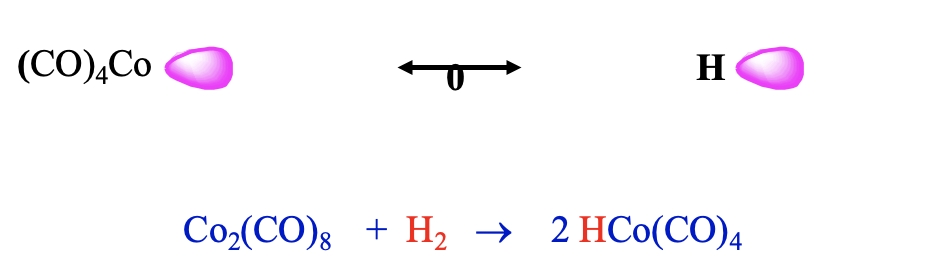
Indeed, one can combine such fragments to form stable carbonyl hydrides such as tetracarbonylhydrido cobalt (0). This molecule can be synthesized by reduction of bis(tetracarbonyl cobalt) (0) with dihydrogen (Fig. \(\PageIndex{13}\)). Counter-intuitively, this molecule is a strong acid, it has an acidity similar to sulfuric acid. One would think that the Co-H bond would be polarized toward H based on electronegativity arguments. However, this is not the case. The carbonyl fragment has a frontier orbital which is energetically higher than that of H, and thus the bond is polarized toward H. In another view we can explain the high acidity be the fact that the loss of the proton leads to the very stable 18 VE tetrahedral Co(CO)4- anion. Thus, loss of the proton occurs easily.
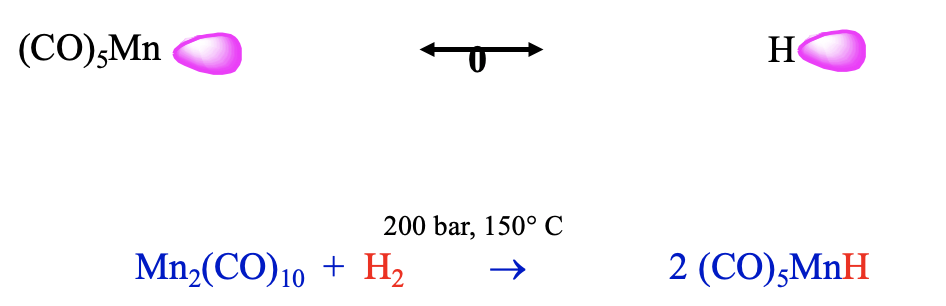
Another 17 VE electron fragment is the Mn(CO)5 fragment. Also this fragment can be combined with an isolobal H fragment to form a stable molecule, which has the composition HMn(CO)5 (Fig. \(\PageIndex{14}\)). It can be prepared from bis(pentacarbonyl manganese) and dihydrogen at 200 bar and 150°C. This carbonyl hydride is a weak acid, it has a similar acidity as H2S. We could argue that this lower acidity may be because the loss of the proton reduces its coordination number from 6 to 5. The coordination number of 6 is the preferred coordination number for carbonyls and thus the tendency to lose the proton is relatively small. The different metal and the number of carbonyl ligands will likely lead to a different energy of the frontier orbital compared to the previous example, which leads to a different polarity.
Overall, one can tune the properties in carbonyl hydrides from highly acidic to hydridic by choice of the metal the coordination number, and also by the choice of additional ligands L other than carbonyl. The electronic and steric properties of the ligands have an influence on the energy of the HOMO of the fragment, and thus on the polarity of the metal-hydrogen bond, and the acidity.


