14.2.3: Migratory Insertion-1,2-Insertions
- Page ID
- 385620
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Insertions of \(\pi\) systems into M-X bonds are appealing in the sense that they establish two new \(\sigma\) bonds in one step, in a stereocontrolled manner. As we saw in the last post, however, we should take care to distinguish these fully intramolecular migratory insertions from intermolecular attack of a nucleophile or electrophile on a coordinated \(\pi\)-system ligand. The reverse reaction of migratory insertion, \(\beta\)-elimination, is not the same as the reverse of nucleophilic or electrophilic attack on a coordinated \(\pi\) system.

Like 1,1-insertions, 1,2-insertions generate a vacant site on the metal, which is usually filled by external ligand. For unsymmetrical alkenes, it’s important to think about site selectivity: which atom of the alkene will end up bound to metal, and which to the other ligand? To make predictions about site selectivity we can appeal to the classic picture of the M–X bond as M + X–. Asymmetric, polarized \(\pi\) ligands contain one atom with excess partial charge; this atom hooks up with the complementary atom in the M–R bond during insertion. Resonance is our best friend here!

A nice study by Yu and Spencer illustrates these effects in homogeneous palladium- and rhodium-catalyzed hydrogenation reactions. Unactivated alkenes generally exhibit lower site selectivity than activated ones, although steric differences between the two ends of the double bond can promote selectivity.
Reactivity Trends in 1,2-Insertions
The thermodynamics of 1,2-insertions of alkenes depend strongly on the alkene, but we can gain great insight by examining the structure of the product alkyl. Coordinated alkenes that give strong metal-alkyl bonds after migratory insertion tend to undergo the process. Hence, electron-withdrawing groups, such as carbonyls and fluorine atoms, tend to encourage migratory insertion—remember that alkyl complexes bearing these groups tend to have stable M–C bonds.
Insertions of alkenes into both M–H and M–R (R = alkyl) are favored thermodynamically, but the kinetics of M–R insertion are much slower. This observation reflects a pervasive trend in organometallic chemistry: M–H bonds react more rapidly than M–R bonds. The same is true of the reverse, \(\beta\)-elimination. Even in cases when both hydride and alkyl elimination are thermodynamically favored, \(\beta\)-hydride elimination is much faster. Although insertion into M–R is relatively slow, this elementary step is critical for olefin polymerizations that form polyalkenes (Ziegler-Natta polymerization). This reaction deserves a post all its own!
As the strength of the M–X bond increases, the likelihood that an L-type \(\pi\) ligand will insert into the bond goes down. Hence, while insertions into M–H and M–C are relatively common, insertions into M–N and M–O bonds are more rare. Lanthanides and palladium are known to promote insertion into M–N in some cases, but products with identical connectivity can come from external attack of nitrogen on a coordinated \(\pi\) ligand. The diastereoselectivity of these reactions provides mechanistic insight—since migratory insertion is syn (see below), a syn relationship between Pd and N is to be expected in the products of migratory insertion. An anti relationship indicates external attack by nitrogen or oxygen.
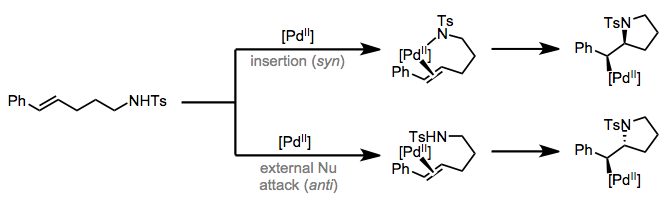
Stereochemistry of 1,2-Insertions
1,2-Insertion may establish two stereocenters at once, so the stereochemistry of the process is critical! Furthermore, 1,2-insertions and \(\beta\)-eliminations are bound by important stereoelectronic requirements. An analogy can be made to the E2 elimination of organic chemistry, which also has strict stereoelectronic demands. For migratory insertion to proceed, the alkene and X-type ligand must be syncoplanar during insertion; as a consequence of this alignment, X and MLn end up on the same face of the alkene after insertion. In other words, insertions into alkenes take place in a syn fashion. Complexes that have difficulty achieving a coplanar arrangement of C=C and M–X undergo insertion very slowly, if at all.
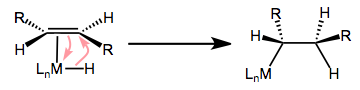
(Michael Evans)
This observation has important implications for \(\beta\)-elimination, too—the eliminating X and the metal must have the ability to align syn.
Insertions of Other \(\pi\) Systems
To close this post, let’s examine insertions into \(\pi\) ligands other than alkenes briefly. Insertions of alkynes into metal-hydride bonds are known, and are sometimes involved in reactions that I refer to collectively as “hydrostuffylation”: hydrosilylation, hydroesterification, hydrogenation, and other net H–X additions across the \(\pi\) bond. Strangely, some insertions of alkynes yield trans products, even though cis products are to be expected from syn addition of M–X. The mechanisms of these processes involve initial syn addition followed by isomerization to the trans complex via an interesting resonance form. The cis complex is the kinetic product, but it isomerizes over time to the more thermodynamically stable trans complex.
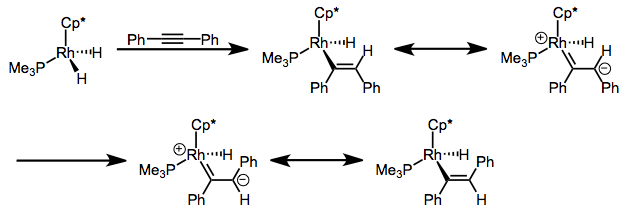
The strongly donating Cp* ligand supports the legitimacy of the zwitterionic resonance form—and suggests that the C=C bond may be weaker than it first appears!
Polyenes can participate in migratory insertion, and insertions of polyenes are usually quite favored because stabilized \(\pi\)-allyl complexes result. In one mind-bending case, a coordinated arene inserts into an M–Me bond in a syn fashion!
Have you ever stopped to consider that the addition of methyllithium to an aldehyde is a formal insertion of the carbonyl group into the Li–Me bond? It’s true! We can think of these as (very) early-metal “insertion” reactions. Despite this precedent, migratory insertion reactions of carbonyls and imines into late-metal hydride and alkyl bonds are surprisingly hard to come by. Rhodium is the most famous metal that can make this happen—rhodium has been used in complexes for arylation and vinylation, for example. Insertion of X=C into the M–R bond is usually followed by \(\beta\)-hydride elimination, which has the nifty effect of replacing H in aldehydes and aldimines with an aryl or vinyl group.


