14.1.3: Reductive Elimination
- Page ID
- 392523
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Reductive Elimination Reactions
Reductive elimination is the microscopic reverse of oxidative addition. The reductive elimination can only occur when the two ligands to be eliminated are in cis-position.
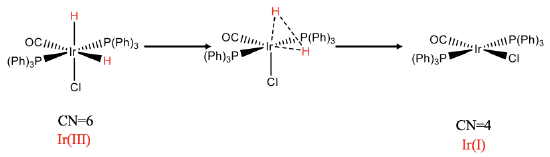
For instance the previously discussed oxidative cis-addition of H2 to the iridium complex is reversible, and the reverse is called the reductive elimination (Fig. \(\PageIndex{1}\)). The cis-orientation of the two hydrido ligands is necessary to form an H-H bond. The reaction can be thought of going along a reaction path in which the Ir-H bonds become gradually larger and and the H-H distance gradually smaller until the H2 molecule is eliminated from the complex.
During reductive elimination, the electrons in the M–X bond head toward ligand Y, and the electrons in M–Y head to the metal. The eliminating ligands are always X-type! On the whole, the oxidation state of the metal decreases by two units, two new open coordination sites become available, and an X–Y bond forms. What does the change in oxidation state suggest about changes in electron density at the metal? As suggested by the name “reductive,” the metal gains electrons. The ligands lose electrons as the new X–Y bond cannot possibly be polarized to both X and Y, as the original M–X and M–Y bonds were. Using these ideas, you may already be thinking about reactivity trends in reductive elimination…hold that thought.
It’s been observed in a number of cases that a ligand dissociates from octahedral complexes before concerted reductive elimination occurs. Presumably, dissociation to form a distorted TBP geometry brings the eliminating groups closer to one another to facilitate elimination.

Square planar complexes may either take on an additional fifth ligand or lose a ligand to form an odd-coordinate complex before reductive elimination. Direct reductive elimination without dissociation or association is possible, too.
Reactivity trends in reductive elimination are opposite those of oxidative addition. More electron-rich ligands bearing electron-donating groups react more rapidly, since the ligands lose electron density as the reaction proceeds. More electron-poor metal centers—bearing π-acidic ligands and/or ligands with electron-withdrawing groups—react more rapidly, since the metal center gains electrons. Sterically bulky ancillary ligands promote reductive elimination since the release of X and Y can “ease” steric strain in the starting complex. Steric hindrance helps explain, for example, why coordination of a fifth ligand to a square planar complex promotes reductive elimination even though coordination increases electron density at the metal center. A second example: trends in rates of reductive eliminations of alkanes parallel the steric demands of the eliminating ligands: C–C > C–H > H–H.

Mechanistic trends for reductive elimination actually parallel trends in mechanisms of oxidative addition, since these two reactions are the microscopic reverse of one another. Non-polar and moderately polar ligands react by concerted or radical mechanisms; highly polarized ligands and/or very electrophilic metal complexes react by ionic (SN2) mechanisms. The thermodynamics of reductive elimination must be favorable in order for it to occur! Most carbon–halogen reductive eliminations, for example, are thermodynamically unfavorable (this has turned out to be a good thing, especially for cross-coupling reactions).
Reductive elimination is an important step in many catalytic cycles—it usually comes near the “end” of catalytic mechanisms, just before product formation. For some catalytic cycles it’s the turnover-limiting step, making it very important to consider! Hydrocyanation is a classic example; in the mechanism of this reaction, reductive elimination of C–CN is the slow step. Electron-poor alkyl ligands, derived from electron-poor olefins like unsaturated ketones, are bad enough at reductive elimination to prevent turnover altogether! Of course, the electronegative CN ligand is not helping things either…how would you design the ancillary ligands L to speed up this step?

Dr. Michael Evans (Georgia Tech)
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


