14.1.1: Ligand Dissociation and Substitution
- Page ID
- 392863
As discussed in Chapter 13, ligand substitution is characterized by a continuum of mechanisms bound by associative (A) and dissociative (D) extremes. At the associative extreme, the first step is an Associative reaction; the incoming ligand forms a bond to the metal and creates an intermediate of higher coordination number. Then the departing ligand takes its lone pair and leaves. At the dissociative extreme, the fist step is a Dissociative reaction and the order of events is opposite; a ligand departs and a new complex with lower coordination number forms. Then, a new ligand associates with the complex in the second step. Sometimes, instead of reacting, the "intermediate" is simply a stable complex with a different coordination number than the reactant.
The most common reactions that are used to create new complexes are Dissociations and Substitutions (involving both Dissociation and Association steps). Associative substitution is common for 16-electron complexes (like \(d^8\) complexes of Ni, Pd, and Pt), while both Dissociation and Dissociative Substitution are the norm for 18-electron complexes. Then again, reality is often more complicated than these extremes. In some cases, evidence is available for interchange (\(I_a\) or \(I_d\)).
In this subsection, we’ll explore ligand substitution reactions and mechanisms in the context of organometallic chemistry. We’d like to be able to (a) predict whether a mechanism is likely to be associative or dissociative; (b) propose a reasonable mechanism from given experimental data; and (c) describe the results we’d expect given a particular mechanism. Keep these goals in mind as you learn the theoretical and experimental nuts and bolts of substitution reactions.
Dissociation
Carbonyl compounds are known to undergo dissociation reactions upon heating or irradiation with light. For example, upon heating, the the cyclopentadienylmolybdenum tricarbonyl dimer (\(\ce{Cp2Mo2(CO)6}\)), where Cp is the cyclopentadienyl ligand) loses a CO ligand from each Mo ion, and a triple bond between the Mo ions is formed (Top, Figure \(\PageIndex{1}\)). An example of a photoactivated dissociation of CO is the case of neutral iron pentacarbonyl, \(\ce{Fe(CO)5}\). Irradiation of \(\ce{Fe(CO)5}\) with UV produces \(\ce{Fe(CO)4}\) (Bottom, Figure \(\PageIndex{1}\)).
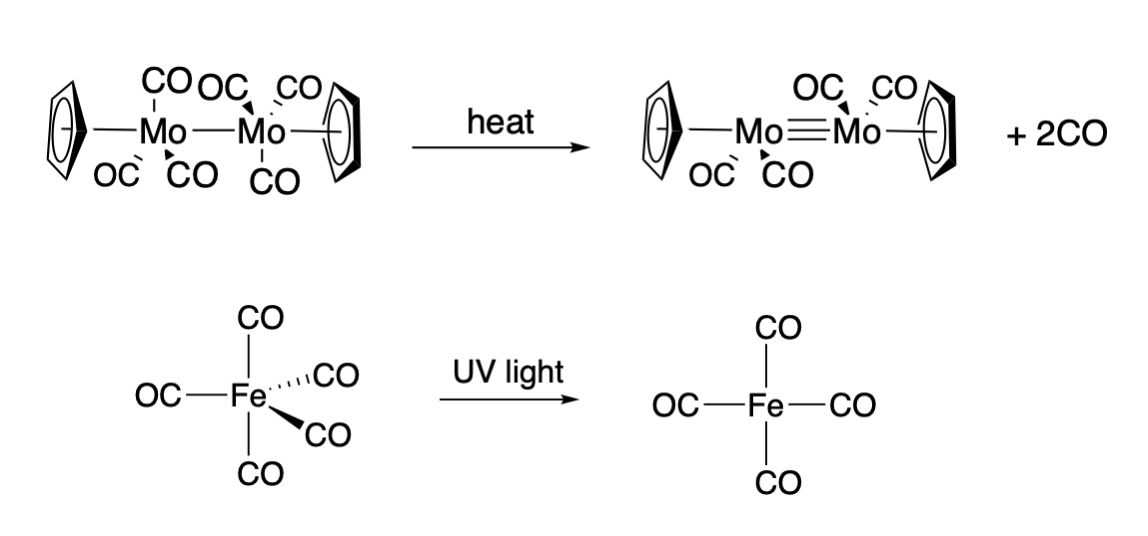
However, in each of the cases shown above, the product complex is reactive toward ligand association, usually resulting in an overall substitution. The cyclopentadienylmolybdenum dicarbonyl dimer shown on the top of Figure \(\PageIndex{1}\) binds a variety of substrates across the metal-metal triple bond. And the iron tetracarbonyl complex shown on the bottom in Figure \(\PageIndex{1}\) readily captures a variety of ligands to result in an overall substitution (example given below); when a ligand doe not associate with it, \(\ce{Fe2(CO)9}\) is produced.
Sources: Iron Pentacarbonyl and Cyclopentadienylmolybdenum tricarbonyl dimer articles from Wikipedia.
Dissociative Substitution
Associative substitution is unlikely for saturated, 18-electron complexes—coordination of another ligand would produce a 20-electron intermediate. For 18-electron complexes, dissociative substitution mechanisms involving 16-electron intermediates are more likely. In a slow step with positive entropy of activation, the departing ligand leaves, generating a coordinatively unsaturated intermediate. The incoming ligand then enters the coordination sphere of the metal to generate the product. For the remainder of this post, we’ll focus on the kinetics of the reaction and the nature of the unsaturated intermediate (which influences the stereochemistry of the reaction). The reverse of the first step, re-coordination of the departing ligand (rate constant k–1), is often competitive with dissociation.
Reaction Kinetics
Let’s begin with the general situation in which \(k_1\) and \(k_{–1}\) are similar in magnitude. Since \(k_1\) is rate limiting, \(k_2\) is assumed to be much larger than \(k_1\) and \(k_{–1}\). Most importantly, we need to assume that variation in the concentration of the unsaturated intermediate is essentially zero. This is called the steady state approximation, and it allows us to set up an equation that relates reaction rate to observable concentrations Hold onto that for a second; first, we can use step 2 to establish a preliminary rate expression.
\[\text{rate} = k_2[L_nM–◊][Li] \tag{1}\]
Of course, the unsaturated complex is present in very small concentration and is unmeasurable, so this equation doesn’t help us much. We need to remove the concentration of the unmeasurable intermediate from (1), and the steady state approximation helps us do this. We can express variation in the concentration of the unsaturated intermediate as (processes that make it) minus (processes that destroy it), multiplying by an arbitrary time length to make the units work out. All of that equals zero, according to the SS approximation. The painful math is almost over! Since Δt must not be zero, the other factor, the collection of terms, must equal zero.
\[ Δ[L_nM–◊] = 0 = (k1[L_nM–L^d] – k–1[L_nM–◊][L^d] – k_2[L_nM–◊][Li])Δt \tag{2}\]
\[0 = k_1[L_nM–Ld] – k_{-1}[L_nM–◊][Ld] – k_2[L_nM–◊][Li] \tag{3}\]
Rearranging to solve for \([L_nM–◊]\), we arrive at the following.
\[ [L_nM–◊] = k_1 \dfrac{[L_nM–L_d]}{(k_{-1}[L_d] + k_2[Li]} \tag{4}\]
Finally, substituting into equation (1) we reach a verifiable rate equation.
\[ \text{rate} = k_2k_1 \dfrac{[L_nM–Ld][Li]}{(k_{-1}[L_d] + k_2[Li]} \tag{5}\]
When \(k_{–1}\) is negligibly small, (5) reduces to the familiar equation (6), typical of dissociative reactions like SN1.
\[\text{rate} = k_1[L_nM–L_d] \tag{6}\]
Unlike the associative rate law, this rate does not depend on the concentration of incoming ligand. For reactions that are better described by (5), we can drown the reaction in incoming ligand to make \(k_2[Li]\) far greater than \(k_{-1}[Ld]\), essentially forcing the reaction to fit equation (6).
The Unsaturated Intermediate & Stereochemistry
Dissociation of a ligand from an octahedral complex generates an usaturated ML5 intermediate. When all five of the remaining ligands are L-type, as in Cr(CO)5, the metal has 6 d electrons for a total electron count of 16. The trigonal bipyramidal geometry presents electronic problems (unpaired electrons) for 6 d electrons, as the figure below shows. The orbital energy levels come from crystal field theory. Distortion to a square pyramid or a distorted TBP geometry removes the electronic issue, and so five-coordinate d6 complexes typically have square pyramidal or distorted TBP geometries. This is just the geometry prediction process in action!
When the intermediate adopts square pyramidal geometry (favored for good π-acceptors and σ-donors…why?), the incoming ligand can simply approach where the departing ligand left, resulting in retention of stereochemistry. Inversion is more likely when the intermediate is a distorted trigonal bipyramid (favored for good π-donors). As we’ve already seen for associative substitution, fluxionality in the five-coordinate intermediate can complicate the stereochemistry of the reaction.
Encouraging Dissocative Substitution
In general, introducing structural features that either stabilize the unsaturated intermediate or destabilize the starting complex can encourage dissociative substitution. Both of these strategies lower the activation barrier for the reaction. Other, quirky ways to encourage dissociation include photochemical methods, oxidation/reduction, and ligand abstraction.
Let’s begin with features that stabilize the unsaturated intermediate. Electronically, the intermediate loves it when its d electron count is nicely matched to its crystal field orbitals. As you study organometallic chemistry, you’ll learn that there are certain “natural” d electron counts for particular geometries that fit well with the metal-centered orbitals predicted by crystal field theory. Octahedral geometry is great for six d electrons, for example, and square planar geometry loves eight d electrons. Complexes with “natural” d electron counts—but bearing one extra ligand—are ripe for dissociative substitution. The classic examples are d8 TBP complexes, which become d8 square planar complexes (think Pt(II) and Pd(II)) upon dissociation. Similar factors actually stabilize starting 18-electron complexes, making them less reactive in dissociative substitution reactions. d6 octahedral complexes are particularly happy, and react most slowly in dissociative substitutions. The three most common types of 18-electron complexes, from fastest to slowest at dissociative substitution, are:
\(d^8\) TBP > \(d^10\) tetrahedral > \(d^6\) octahedral
Destabilization of the starting complex is commonly accomplished by adding steric bulk to its ligands. Naturally, dissociation relieves steric congestion in the starting complex. Chelation has the opposite effect, and tends to steel the starting complex against dissociation.
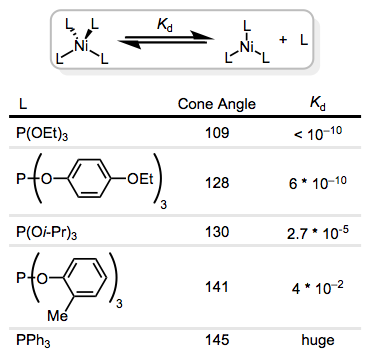
I plan to cover the “quirky” methods in a post of their own, but these include strategies like N-oxides for CO removal, photochemical cleavage of the metal–departing ligand bond, and the use of silver cation to abstract halide ligands. Oxidation and reduction can also be used to encourage substitution: 17- and 19-electron complexes are much more reactive toward substitution than their 18-electron analogues.
Associative Substitutions
Despite the sanctity of the 18-electron rule in organometallic chemistry, a wide variety of stable complexes possess fewer than 18 total electrons at the metal center. Perhaps the most famous examples of these complexes are 14- and 16-electron complexes of group 10 metals (Ni, Pt, Pd). Ligand substitution in complexes of this class typically occurs via an associative mechanism, involving approach of the incoming ligand to the complex before departure of the leaving group. If we keep this principle in mind, it seems easy enough to predict when ligand substitution is likely to be associative. But how can we spot an associative mechanism in experimental data, and what are some of the consequences of this mechanism?
The prototypical mechanism of associative ligand substitution. The first step is rate-determining. A typical mechanism for associative ligand substitution is shown above. It should be noted that square pyramidal geometry is also possible for the intermediate, but is less common. Let’s begin with the kinetics of the reaction.
Reaction Kinetics for Associative Reactions
Reaction kinetics are commonly used to elucidate organometallic reaction mechanisms, and ligand substitution is no exception. Different mechanisms of substitution may follow different rate laws, so plotting the dependence of reaction rate on concentration often allows us to distinguish mechanisms. Associative substitution’s rate law is analogous to that of the SN2 reaction—rate depends on the concentrations of both starting materials.
\[ L_nM–L^d + L_i → L_nM–L_i + L^d \]
\[ \dfrac{d[L_nM–L^i]}{dt} = rate = k_1[L_nM–L^d][L^i] \]
The easiest way to determine this rate law is to use pseudo-first-order conditions. Although the rate law is second order overall, if we could somehow render the concentration of the incoming ligand unchanging, the reaction would appear first order. The observed rate constant under these conditions reflects the constancy of the incoming ligand’s concentration (\(k_{obs} = k_1[L^i]\), where both \(k_1\) and \([Li]\) are constants). How can we make the concentration of the incoming ligand invariant, you ask? We can drown the reaction in ligand to achieve this. The teensy weensy bit actually used up in the reaction has a negligible effect on the concentration of the “sea” of starting ligand we began with. The observed rate is equal to \(k_{obs}[L_nM–L^d]\), as shown by the purple trace below. By determining \(k_{obs}\) at a variety of \([L^i]\) values, we can finally isolate \(k_1\), the rate constant for the slow step. The red trace below at right shows the idea.
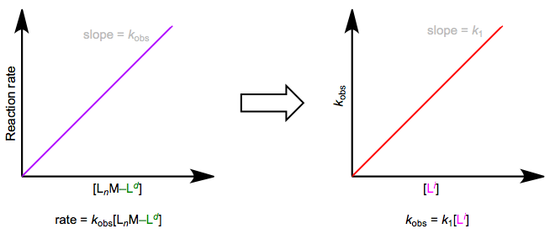
In many cases, the red trace ends up with a non-zero y-intercept…curious, if we limit ourselves to the simple mechanism shown in the first figure of this post. A non-zero intercept suggests a more complex mechanism. We need to add a new term (called \(k_s\) for reasons to become clear shortly) to our first set of equations:
\[rate = (k_1[L_i] + k_s)[L_nM–L^d]\]
\[k_{obs} = k_1[L_i] + k_s\]
The full rate law suggests that some other step (with rate ks[LnM–Ld]) independent of incoming ligand is involved in the mechanism. To explain this observation, we can invoke the solvent as a reactant. Solvent can associate with the complex first in a slow step, then incoming ligand can displace the solvent in a fast step. Solvent concentration doesn’t enter the rate law because, well, it’s drowning the reactants and its concentration undergoes negligible change! An example of this mechanism in the context of Pt(II) chemistry is shown below.
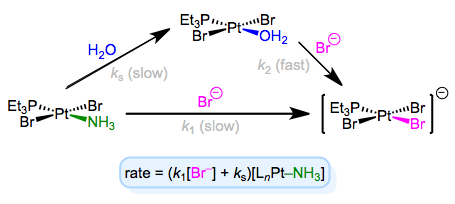
As an aside, it’s worth mentioning that the entropy of activation of associative substitution is typically negative. Entropy decreases as the incoming ligand and complex come together in the rate-determining step. Dissociative substitution shows the opposite behavior: loss of the departing ligand in the RDS increases entropy, resulting in positive entropy of activation.
Stereochemistry of Associative Substitution
As we saw in discussions of the trans effect, the entering and departing ligands both occupy equatorial positions in the trigonal bipyramidal intermediate. Microscopic reversibility is to blame: the mechanism of the forward substitution (displacement of the leaving by the incoming ligand) must be the same as the mechanism of the reverse reaction (displacement of the incoming by the leaving ligand). This can be a confusing point, so let’s examine an alternative mechanism that violates microscopic reversibility.
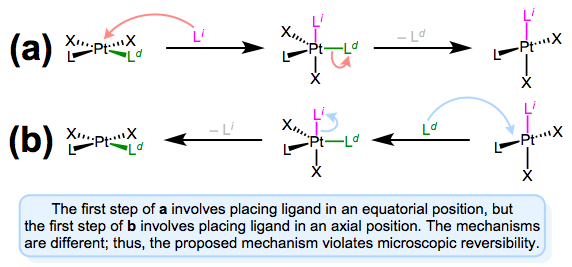
The figure above shows why a mechanism involving axial approach and equatorial departure (or vice versa) is not possible. The forward and reverse reactions differ, in fact, in both steps. In forward mechanism a, the incoming ligand enters an axial site. But in the reverse reaction, the incoming ligand (viz., the departing ligand in mechanism a) sits on an equatorial site. The second steps of each mechanism differ too—a involves loss of an equatorial ligand, while b involves loss of an axial ligand. Long story short, this mechanism violates microscopic reversibility. And what about a mechanism involving axial approach and axial departure? Such a mechanism is unlikely on electronic grounds. The equatorial sites are more electron rich than the axial sites, and σ bonding to the axial \(d_{z^2}\) orbital is expected to be strong. Intuitively, then, loss of ligand from an axial site is less favorable than loss from an equatorial site.
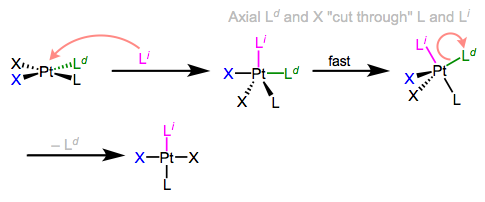
I know what you’re thinking: what the heck does all of this have to do with stereochemistry? Notice that, in the equatorial-equatorial mechanism (first figure of this post), the axial ligands don’t move at all. The configuration of the starting complex is thus retained in the product. Although retention is “normal,” complications often arise because five-coordinate TBP complexes—like other odd-coordinate organometallic complexes—are often fluxional. Axial and equatorial ligands can rapidly exchange through a process called Berry pseudorotation, which resembles the axial ligands “cutting through” a pair of equatorial ligands like scissors (animation!). Fluxionality means that all stereochemical bets are off, since any ligand can feasibly occupy an equatorial site. In the example below, the departing ligand starts out cis to L, but the incoming ligand ends up trans to L.
Associative Substitution in 18-electron Complexes?
Associative substitution can occur in 18-electron complexes if it’s preceded by the dissociation of a ligand. For example, changes in the hapticity of cyclopentadienyl or indenyl ligands may open up a coordination site, which can be occupied by a new ligand to kick off associative substitution. An allyl ligand may convert from its π to σ form, leaving an open coordination site where the π bond left. A particularly interesting case is the nitrosyl ligand—conversion from its linear to bent form opens up a site for coordination of an external ligand.
Summary of Associative Substitution
Associative ligand substitution is common for complexes with 16 total electrons or fewer. The reaction is characterized by a second-order rate law, the possibility of solvent participation, and a trigonal bipyramidal intermediate that is often fluxional. An open coordination site is essential for associative substitution, but such sites are often hidden in the dynamism of 18-electron complexes with labile ligands.
Quirky Substitutions
Over the years, a variety of “quirky” substitution methods have been developed. All of these have the common goal of facilitating substitution in complexes that would otherwise be inert. It’s an age-old challenge: how can we turn a stable complex into something unstable enough to react? Photochemical excitation, oxidation/reduction, and radical chains all do the job, and have all been well studied. We’ll look at a few examples in this post—remember these methods when simple associative or dissociative substitution won’t get the job done.
Photochemical Substitution
Substitution reactions of dative ligands—most famously, CO—may be facilitated by photochemical excitation. We just discussed the photochemically-activated dissociation of CO from ironpentacarbonyl above; that reaction is often used to accomplish substitution of a CO ligand. Other CO complexes also undergo photochemically-activated CO substitution reactions. Two examples are shown below. The first reaction yields only monosubstituted product without ultraviolet light, even in the presence of a strongly donating phosphine.
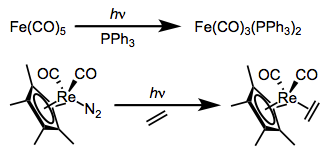
All signs point to dissociative mechanisms for these reactions (the starting complexes have 18 total electrons each). Excitation, then, must increase the M–L antibonding character of the complex’s electrons; exactly how this increase in antibonding character happens has been a matter of some debate. Originally, the prevailing explanation was that the LUMO bears M–L antibonding character, and excitation kicks an electron up from the HOMO to the LUMO, encouraging cleavage of the M–L bond. A more recent, more subtle explanation backed by calculations supports the involvement of a metal-to-ligand charge-transfer state along with the “classical” ligand-field excited state.
Oxidation/Reduction
Imagine a screaming baby without her pacifier—that’s a nice analogy for an odd-electron organometallic complex. Complexes bearing 17 and 19 total electrons are much more reactive toward substitution than their even-electron counterparts. Single-electron oxidation and reduction (“popping out the pacifier,” if you will) can thus be used to efficiently turn on substitution. As you might expect, oxidation and reduction work best on electron-rich and electron-poor complexes, respectively. The Mn complex in the oxidative example below, for instance, includes a strongly donating MeCp group (not shown).
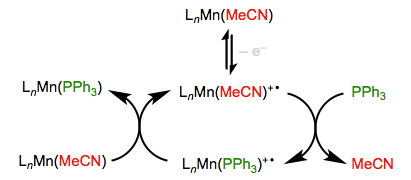
Reduction works well for electron-poor metal carbonyl complexes, which are happy to accept an additional electron.
There is a two-electron oxidation method that’s also worth knowing: the oxidation of CO with amine oxides. This nifty little method releases carbon dioxide, amine, and an unsaturated complex that may be quenched by a ligand hanging around. The trick is addition to the CO ligand followed by elimination of the unsaturated complex. As the oxidized CO2 and reduced amine float away, the metal complex finds another ligand.
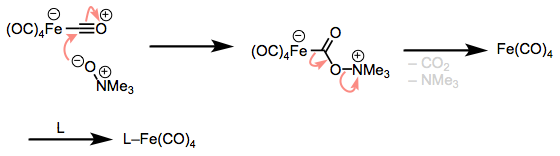
Radical Chain Processes
Atom abstraction from 18-electron complexes produces neutral 17-electron intermediates, which are susceptible to ligand substitution via radical chain mechanisms. The fact that the intermediates are neutral distinguishes these methods from oxidation-based methods. First-row metal hydrides are great for these reactions, owing to their relatively weak M–H bonds. One example is shown below.
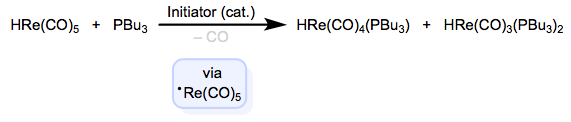
After abstraction of the hydrogen atom by initiator, substitution is rapid and may occur multiple times. Propagation begins anew when the substituted radical abstracts hydrogen from the starting material to regenerate the propagating radical and form the product. These quirky methods are nice to have in your back pocket when you’re backed into a synthetic corner—sometimes, conventional associative and dissociative substitution just won’t do the job. In the next post, we’ll press on to oxidative addition.