13.3.2: Simplifying the Organometallic Complex by Deconstruction
- Page ID
- 385576
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Organometallic complexes, which consist of centrally located metals and peripheral organic compounds called ligands, are the workhorses of organometallic chemistry. Just like organic intermediates, understanding something about the structure of these molecules tells us a great deal about their expected reactivity. Some we would expect to be stable, and others definitely not! A big part of our early explorations will involve describing, systematically, the principles that govern the stability of organometallic complexes. From the outset, I will say that these principles are not set in stone and are best applied to well controlled comparisons. Nonetheless the principles are definitely worth talking about, because they form the foundation of everything else we’ll discuss. Let’s begin by exploring the general characteristics of organometallic complexes and identifying three key classes of organic ligands.
When we think of metals we usually think of electropositive atoms or even positively charged ions, and many of the metals of OM chemistry fit this mold. In general, it is useful to imagine organic ligands as electron donors and metals as electron acceptors. When looking at a pair of electrons shared between a transition metal and main-group atom (or hydrogen), I imagine the cationic metal center and anionic main-group atom racing toward one another from oblivion like star-crossed lovers. In the opposite direction (with an important caveat that we’ll address soon), we can imagine ripping apart metal–R covalent bonds and giving both electrons of the bond to the organic atom. This heterolytic bond cleavage method reproduces the starting charges on the metal and ligand. Unsurprisingly, the metal is positive and the ligand negative.
FYI, you might see the blue bipyridine referred to as an L2 ligand elsewhere; this just means that a single bipyridine molecule possesses two L-type binding points. Ligands with multiple binding points are also known as chelating or polydentate ligands. Chelating ligands may feature mixed binding modes; for instance, the allyl ligand is of the LX-type. Chelating ligands can also bind to two different metal centers; when they act in this way, they’re called bridging ligands. But don’t let all this jargon throw you! Deconstruct complexes one binding point at a time, and you cannot go wrong.
Next, we’ll take a closer look at the metal center and expand on the purpose of the deconstruction process described here.
"Bookkeeping" through deconstruction of organometallic complexes
Now it’s time to turn our attention to the metal center, and focus on what the deconstruction process can tell us about the nature of the metal in organometallic complexes. Let’s turn our attention now to a new complex. I’ve gone ahead and deconstructed it for us.
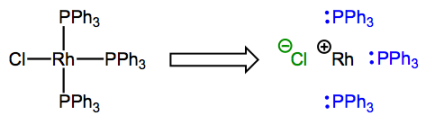
Say hello to rhodium (Rh)! Don't fret; it's just a group 9 element.
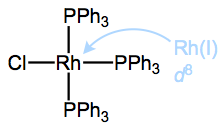
The complex possesses one X-type and three L-type ligands, so the rhodium atom ends up with a formal charge of +1. The formal charge on the metal center after deconstruction has a very special name that you will definitely want to commit to memory: it’s called the oxidation state. It’s usually indicated with a roman numeral next to the atomic symbol of the metal (the “+” is implied). In the complex shown above, rhodium is in the Rh(I) or +1 oxidation state. Oxidation state is most useful because changes in oxidation state indicate changes in electron density at the metal center, and this can be a favorable or unfavorable occurrence depending on the other ligands around. We will see this principle in action many, many times! Get used to changes in oxidation state as everyday events in organometallic reaction mechanisms. Unlike carbon (with the exception of carbene…what’s its oxidation state?!) and other second-row elements, the transition metals commonly exhibit multiple different oxidation states. More on that later, though. For now, training yourself to rapidly identify the oxidation state of a complexed metal is most important. Please note that when a complex possesses an overall charge, the oxidation state is affected by this charge!
oxidation state = number of X-type ligands bound to metal + overall charge of complex
What of this number of d electrons concept? A very useful way to think about “number of d electrons” is as the “number of non-bonding electrons on the metal center,” and you’re probably familiar with identifying non-bonding electrons from organic chemistry. The numbers of valence electrons of each organic element are set in stone: carbon has four, nitrogen has five, et cetera. Furthermore, using this knowledge, it’s straightforward to determine the number of lone pair electrons associated with an atom by subtracting its number of covalent bonds from its total number of valence electrons. E.g., for a neutral nitrogen atom in an amine NR3, 5 – 3 = 2 lone pair electrons, typically. The extension to organometallic chemistry is natural! We can analyze complexed metal centers in the same way, but they tend to have a lot more non-bonding electrons than organic atoms, and the number depends on the metal’s oxidation state. For instance, the deconstructed rhodium atom in the figure above has 8 d electrons: 9 valence electrons minus 1 used for bonding to Cl. Dative bonds don’t affect d electron count since both electrons in the bond come from the ligand.
number of non-bonding electrons = number of d electrons = metal’s group number – oxidation state
Drawing all the non-bonding d electrons out as lone pairs would clutter things up, so they are never drawn…but we must remember that they’re around! Why? Because the number of d electrons profoundly affects a complex’s geometry. We will return to this soon, but the key idea is that the ligands muck up the energies of the d orbitals as they approach the metal (recall the “star-crossed lovers” idea), and the most favorable way to do so depends on the number of non-bonding electrons on the metal center.
Oxidation state and d electron count: two tools the OM chemist can't live without!
This post introduced us to two important bookkeeping tools, oxidation state and number of d electrons. In the final installment of the “Simplifying the Organometallic Complex” series, we’ll bring everything together and discuss total electron count. We’ll see that total electron count may be used to draw a variety of insightful conclusions about organometallic complexes.
Apply deconstruction to gain insight
So far, we’ve seen how deconstruction can reveal useful “bookkeeping” properties of organometallic complexes: number of electrons donated by ligands, coordination number, oxidation state, and d electron count (to name a few). Now, let’s bring everything together and discuss total electron count, the sum of non-bonding and bonding electrons associated with the metal center. Like oxidation state, total electron count can reveal the likely reactivity of OM complexes—in fact, it is often more powerful than oxidation state for making predictions. We’ll see that there is a definite norm for total electron count, and when a complex deviates from that norm, reactions are likely to happen.
Let’s begin with yet another new complex. This molecule features the common and important cyclopentadienyl and carbon monoxide ligands, along with an X-type ethyl ligand.
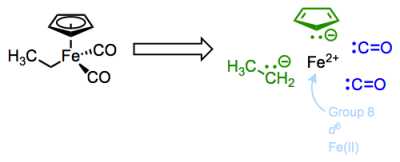
What is the total electron count of this Fe(II) complex?
The Cp or cyclopentadienyl ligand is a polydentate, six-electron L2X ligand. The two pi bonds of the free anion are dative, L-type ligands, which we’ll see again in a future post on ligands bound through pi bonds. Think of the electrons of the pi bond as the source of a dative bond to the metal. Since both electrons come from the ligand, the pi bonds are L-type binders. The anionic carbon in Cp is a fairly standard, anionic X-type binder. The carbon monoxide ligands are interesting examples of two-electron L-type ligands—notice that the free ligands are neutral, so these are considered L-type! Carbon monoxide is an intriguing ligand that can teach us a great deal about metal-ligand bonding in OM complexes…but more on that later.
After deconstruction, we see that the Fe(II) center possesses 6 non-bonding d electrons. The total electron count is just the d electron count plus the number of electrons donated by the ligands. Since the d electron count already takes overall charge into account, we need not worry about it as long as we’ve followed the deconstruction procedure correctly.
total electron count = number of d electrons + electrons donated by ligands
For the Fe(II) complex above, the total electron count is thus 6 + (6 + 2 + 2 + 2) = 18. Let’s work through another example: the complex below features an overall charge of +1. Water is a dative ligand—that “2″ is very important!
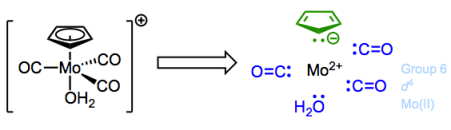
Note that the overall charge is lumped into the oxidation state and d electron count of Mo.
The oxidation state of molybdenum is +2 here…remember that the overall charge factors in to that. When everything is said and done, the total electron count is 4 + (6 + 2 + 2 + 2 + 2) = 18.
What’s up with 18?! As it turns out, 18 electrons is a very common number for stable organometallic complexes. So common that the number got its own rule—the 18-electron rule—which states that stable transition-metal complexes possess 18 or fewer electrons. The rule is analogous to organic chemistry’s octet rule. The typical explanation for the 18-electron rule points out that there are 9 valence orbitals (1 s, 3 p, 5 d) available to metals, and using all of these for bonding seems to produce the most stable complexes. Of course, as soon as the rule left the lips of some order-craving chemist, researchers set out to find counterexamples to it, and a number of counterexamples are known. Hartwig describes the rule as an “empirical guideline” with little theoretical support. In fact, theoretical studies have shown that the participation of p orbitals in complex MOs is unlikely. I know that’s not what you want to hear—but hang with me! The 18-electron rule is still a very useful guideline. It’s most interesting, in fact, when it is not satisfied.
One last example…how would you expect the complex below to react?
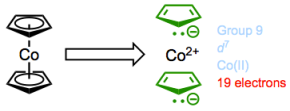
Cobaltocene: jonesing for chemical change.
If we assume that the 18-electron rule is true, then cobaltocene has a real problem. It possesses 7 + (6 + 6) = 19 total valence electrons! Yet, we can also reason that this complex will probably react to relieve the strain of not having 18 electrons by giving up an electron. Guess what? In practice, cobaltocene is a great one-electron reducing agent, and can be used to prepare anionic complexes through electron transfer.
\[CoCp_2 + ML_n → [CoCp_2]+[ML_n]^–\]
This post described how to calculate total electron count and introduced the power of the 18-electron rule for predicting whether a complex will donate or accept electrons. We will definitely see these ideas again! But what happens when the electron counts of two complexes we’re interested in comparing are the same? We’ll need more information. In the next post, we’ll explore the periodic trends of the transition series. Our goal will be to make meaningful comparisons between complexes of different metals.


