13.4.1: Carbon Monoxide (Carbonyl Complexes)
- Last updated
- Save as PDF
- Page ID
- 385580
Introduction into Carbonyl Complexes
In this chapter we will look closer at carbonyl complexes, often just called carbonyls. Why? They are interesting for a number of reasons. Firstly, they are a quite extensive class of compounds with a diverse coordination chemistry. We will learn that the CO ligand can bind to a metal in various, sometimes non-obvious ways. Further, carbonyls are frequently used as starting materials for other coordination compounds. This is because the carbonyl ligand has no charge and carbon monoxide is a gas. Because of that a ligand substitution reaction can be easily driven to the right side by purging CO out of the reaction vessel. CO is a C1 unit, and this is frequently used in catalysis with carbonyls. Carbonyls are often intermediates in reactions that add a single carbon atom to a hydrocarbon chain. A fascinating fundamental property of carbonyls is that its \(\pi\)-accepting properties stabilize metals in low, sometimes even negative oxidation numbers.
Bonding in CO
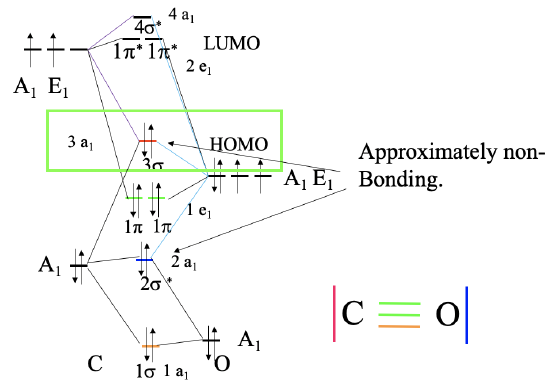
Figure \(\PageIndex{1}\): Bonding in the CO molecule. MO diagram (left), and corresponding valence bond structure (right). For more explaination click here.
The carbon in the CO molecule is the more reactive end, and thus CO prefers to bind with the carbon to a metal, and not with oxygen. This is not obvious because the carbon is less electronegative than oxygen. The reason is that the HOMO of the CO molecule is an approximately non-bonding orbital which is primarily localized at the carbon (Figure \(\PageIndex{1}\)). In the valence bond picture it is resembled by the electron-lone pair at the carbon atom. The electron lone pair at the oxygen is resembled by the 2a1 molecular orbital which has a significantly lower energy, therefore it is rarely used in bonding. Both the \(\pi\) and \(\pi\)*-orbitals are relatively close in energy to the HOMO, and thus these orbitals can also be used for bonding in carbonyls. This explains the diverse coordination chemistry of carbonyls.
σ-binding Modes of The Carbonyl Ligand

In the most simple case the CO uses its electron lone pair at the carbon to bind to single metal atom M (Figure \(\PageIndex{2}\)). In this case we call CO a terminal carbonyl ligand. In addition, it is possible that the electron lone pair is shared between two or even three metals that are interconnected via metal-metal bonds. In these cases, we say that the CO acts as a \(\mu\)-bridged, and \(\mu_3\)-brigded ligand, respectively. If two metals held together by a metal-metal bond are different, then the interaction of CO with one metal may be stronger than with the other. In this case the CO ligand acts as a semibridging ligand. In all these cases CO acts as a 2-electron donor because it donates its two electrons in the electron lone pair in the carbon atom.
In addition to the electron lone pair at the carbon the CO ligand can also use its binding \(\pi\)-orbitals for electron-donation into metal orbitals (Figure \(\PageIndex{3}\)). However, these electrons can only be used in conjunction with the electron lone pair at C because the electron pair has a higher energy than the \(\pi\)-electrons, and electrons of higher energy are always used first. For steric reasons the electron lone pair and the \(\pi\)-electrons are always donated to different metals that are held together by metal-metal bonds.
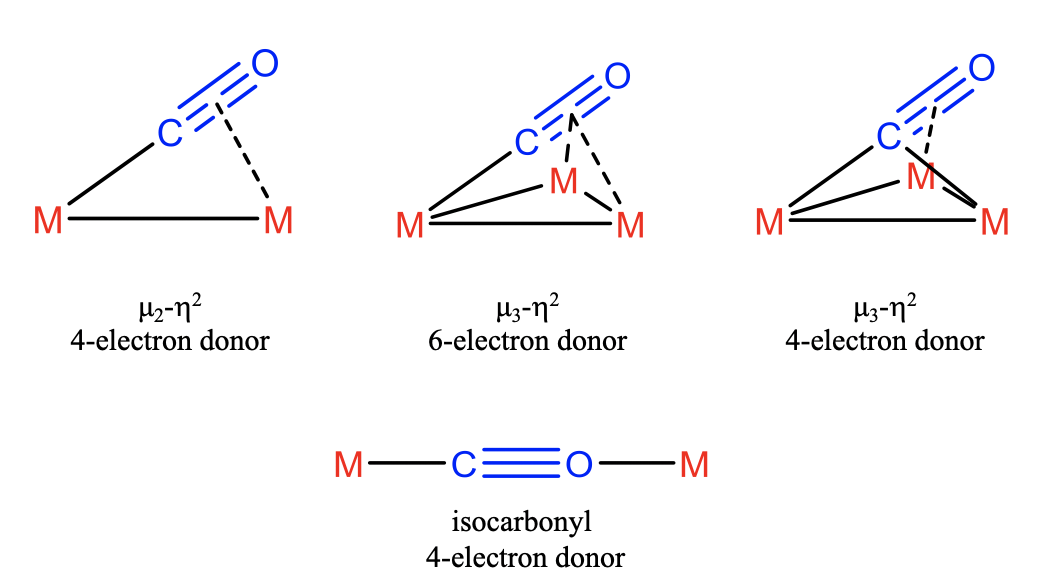
In the most simple case the CO ligand binds in \(\mu_2\)-\(\eta_2\)-mode which implies that the electron lone pair binds to one metal and two \(\pi\)-electrons bind to another. In this this case the CO ligand acts as a 4-electron donor. In addition, it is possible that all four \(\pi\)-electrons are involved involved in the bonding in addition to the electron lone pair. In this case three metal atoms are involved. The first one interacts with the electron-lone pair, the second one with the two \(\pi\)-electrons, and the third one with the other two \(\pi\)-electrons. Because three metals are bridged and both atoms of the ligand are involved in the bonding with the metal we can say that CO binds in \(\mu_3\)-\(\eta_2\)-fashion and acts as a 6-electron donor. It is also possible that the electron-lone pair is being shared between two metals, and two \(\pi\)-electrons are donated to the third metal. Also in this case the ligand binds in \(\mu_3\)-\(\eta_2\)-fashion, but acts as a 4-electron donor. Another way the CO ligand can act as 4-electron donor is when it acts as an isocarbonyl ligand. In this case it uses its electron pairs at both the C and the O-atoms. This is only possible when steric circumstances favor the utilization of the O-electron lone pair over the energetically higher \(\pi\)-electrons. This is rare.
\(\pi\)-binding Modes of The Carbonyl Ligand
The carbonyl ligand can use its \(\pi\)*-orbitals for bonding with metal d-orbitals in \(\pi\)-fashion. The ligand acts as a \(\pi\)-acceptor. There are two possibilities for the binding (Figure \(\PageIndex{4}\)).
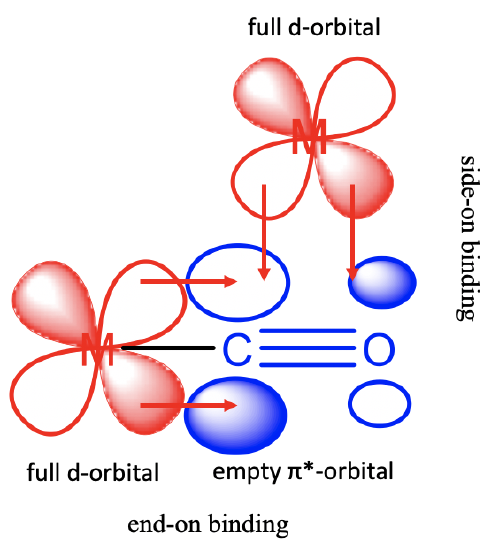
The first one occurs when the CO-ligand acts as a terminal ligand binding end-on. In this case the two lobes of the \(\pi\)*-orbitals at the carbon interact with the the lobes of a metal d-orbital. Also the bonding \(\pi\)-orbitals have the right symmetry to overlap with the metal d-orbital in this mode, but their energies are much further away from those of the d-orbitals, so that these interactions can be neglected. The second possibility is that the CO binds side-on to the a metal-d-orbital. In this case one lobe at C and one lobe at O interacts with the metal d-orbital. These interactions are less strong compared to the end-on interactions because the orbital overlap is less efficient due to the unequal size of the lobes of the \(\pi\)*-orbital. The \(\pi\)*-orbital is mostly localized at the carbon-atom because the carbon atom is the more electropositive atom. Note that the bonding \(\pi\)-orbitals do not have the right symmetry to overlap with a metal-d orbital in \(\pi\)-fashion, they can only overlap in σ-fashion when the binding is side-on.
The Dewar-Chatt-Duncanson model
The σ-donor and the \(\pi\)-acceptor interactions in carbonyl complexes synergistically reinforce each other. This synergistic effect is called the Dewar-Chatt-Duncanson model for carbonyls. How can we understand the synergistic interactions. Let us consider a carbonyl ligand that binds end-on to a metal.

Let us first look at the σ-donor interactions. The electron lone pair at the carbon donates electron density into empty metal d-orbitals and a dative bond is formed between the metal and the carbon. The donated electron density enhances the energy of the metal d-electrons due to increased electron-electron repulsion. Because of their increased energy the d-electrons get more easily accepted by the carbonyl ligand through the \(\pi\)-acceptor interactions. The \(\pi\)-acceptor interactions increase the bond order between the metal and the carbon bond. At the same time the bond order between carbon and oxygen gets decreases because electron density has been transferred from the metal into the \(\pi\)*-orbitals (Figure \(\PageIndex{5}\)).
The strength of the \(\pi\)-acceptor interactions can differ significantly in carbonyls. One can draw three different structures for weak, intermediate, and strong \(\pi\)-acceptor interactions (Figure \(\PageIndex{6}\) to \(\PageIndex{8}\)).

When only weak interactions are present we can represent the M-C bond as a single bond, and the C-O bond as a triple bond.

When the interactions have intermediate strength we can represent both the M-C bond and the C-O bond as a double-bonds.

When the \(\pi\)-acceptor interactions are strong then the M-C bond becomes a triple bond and the C-O bond becomes a single bond.
On what does the strength of the \(\pi\)-acceptor interactions depend? It depends mostly on the charge on the carbonyl. Carbonyl cations with a charge of +2 or higher tend to have weak \(\pi\)-acceptor interactions. Neutral carbonyls or carbonyls with a +1 or -1 charge have intermediate \(\pi\)-acceptor interactions. and those with a negative charge of 2- or higher have strong \(\pi\)-acceptor interactions. One can see from this that the smaller the positive charge and the higher the negative charge, the higher the metal-carbon bond-order, and the stronger the metal-carbon bond. As a consequence negative charges tend to stabilize carbonyls, while positive charges destabilize them. Therefore, carbonylate anions tend to be more stable compared to carbonyl cations. The stability of neutral carbonyls is intermediate.
Homoleptic Carbonyls of The Transition Metals
After having understood the principles of the bonding in carbonyls let us next think about what structures transition metal carbonyls make. The structures follow mostly the 18 electron rule. For the most simple homoleptic carbonyls, in which the carbonyl ligand binds end-on to the transition metal acting as a two-electron donor, we would just assemble as many ligands as needed until we have 18 electrons. This would give us the coordination number in the carbonyl from which we could deduct the structure. This works well for transition metals with an even number of valence electrons.

In this case the number of ligands x is just 18 minus the number of metal electrons divided by 2. We would therefore expect a mononuclear carbonyl of the type M(CO)x (Figure \(\PageIndex{9}\)). For metals with an odd number of electrons, the situation is more complicated because an odd number times two multiplied with an integer number never gives 18. In this case, as many ligands x as needed to make a 17 valence electron complex are added to the metal, and then the 17 valence electron complex dimerizes to form a dinuclear carbonyl of the composition M2(CO)x. An exception is the vanadium. It makes a 17 valence electron vanadium hexacarbonyl that does not dimerize because a coordination number of 7 is not favorable.
Homoleptic carbonyls of the 6th group (M = Cr, Mo, W)
Now let us look closer at the carbonyls with metals with an even number of electrons. We can start out with group 6 which contains the elements chromium, molybdenum, and tungsten. Our task is to determine the composition and structure of the carbonyls.

According to the 18 electron rule we need 18 electrons overall. How many are contributed by the metal? Because the metals are in group 6, they all have six electrons. The carbonyls carry no charge, so there are no electrons to be subtracted or added. How many ligand electrons do we need to get to 18? Well, that is 18-6=12 electrons. How many carbonyl ligands are needed then? Because each ligand is considered a two electron donor, we need 12/2=6 ligands. The composition of the carbonyl will therefore be M(CO)6. The carbonyl adopts octahedral shape in order to maximize the distance of the ligands from each other. The group 6 carbonyls are colorless, crystalline, and sublimable solids.
Charged Octahedral Carbonyls with 18 Electrons
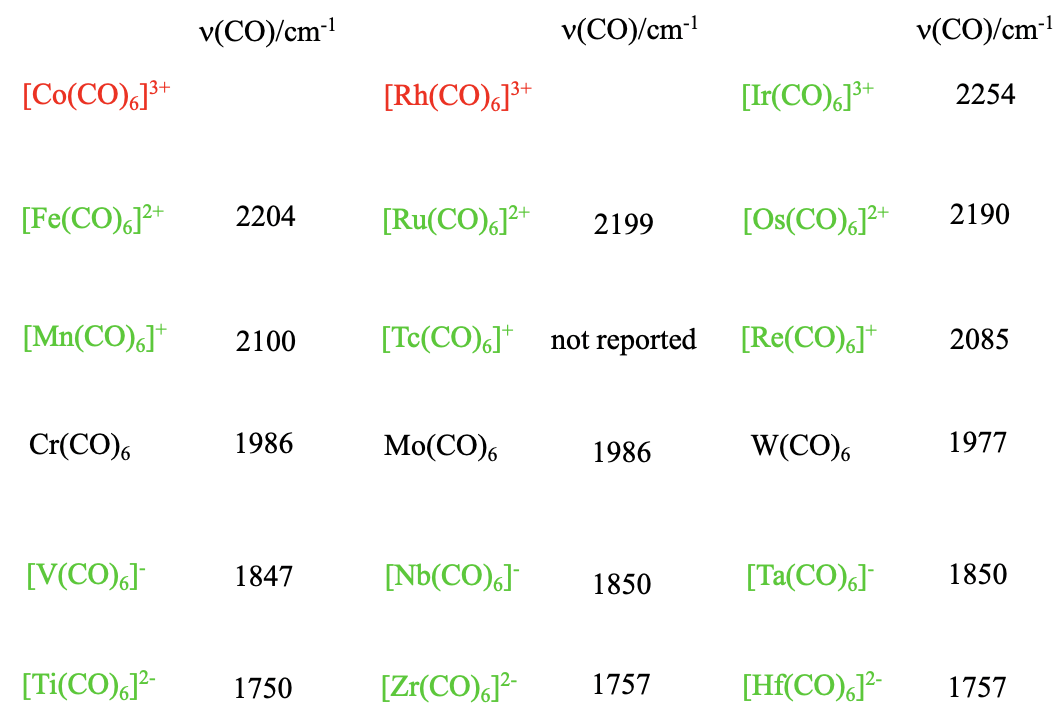
Are there also other 18 e carbonyls of the type M(CO)6 with other metals but group 6 metals? Yes, but the charge at the carbonyl needs to be adjusted so that the complex has 18 electrons. For instance, we can replace Cr by V, but then the we need a 1- charge which results in a carbonylate of the formula V(CO)6-. Why? The vanadium is in group 5 and has one electron less than chromium. For that reason, we must add an electron which gives the complex a 1- charge. Also the higher homologues Nb(CO)6- and Ta(CO)6- are known. What if we go further to the left in the periodic table? Titanium is left to the vanadium, and has four valence electrons. Therefore, the 18 valence electron hexacarbonyl of titanium has a 2- charge, and the formula is Ti(CO)62-. Again, the higher homologues of Ti(CO)62- , the Zr(CO)62- and the Hf(CO)62- are also known. Can we also go to the right in the periodic table? Manganese sits to the right of the chromium. The manganese has one electron more than the chromium, therefore the 18 electron hexacarbonyl of manganese must be a carbonyl cation with a 1+ charge, and the formula is Mn(CO)62+. Of the higher homologues, both the Tc(CO)6+ and the Re(CO)6+ are known, too. To the right of the Mn, there is the Fe which has 8 valence electrons. Therefore the 18 electron iron hexacarbonyl must have a 2+ charge, and the formula is Fe(CO)62+. The higher homologues Ru(CO)62+ and Os(CO)62+ are also known. Can we go even further to the left, to the Co? The expected formula for Co carbonyl would be Co(CO)63+, but it is not known, and neither is the higher homologue, the Rh(CO)63+. Only the Ir(CO)63+ has been isolated. This reflects a general trend in carbonyl chemistry. Positive charges destabilize the carbonyl, and carbonyls with high positive charges are frequently not stable. On the other hand, negative charges stabilize a carbonyl and even carbonylates with high negative charges are stable. We can easily explain this by the fact that the bond order between the metal and the carbon decreases with increasing positive charge, and increases with increasing negative charge. Increasing bond order strengthens the stability of the carbonyl. We see from this that the \(\pi\)-acceptor properties are quite important for the stability of carbonyls. We also see that in carbonylates the oxidation numbers of the metals are negative. Negative oxidation numbers are quite unusual for metals. We conclude that the carbonyl ligand has the unusual property to stabilize the metal in negative oxidation states.
Is there a way to easily measure the bond order of an M-C bond? We can do this indirectly by measuring the IR-spectrum of the carbonyl. Because the bond order of the C-O bond decreases with increasing bond order for the M-C bond, the wavenumber for the C-O stretch vibration can be used as a measure for the M-C bond order. The lower the wavenumber, the lower the C-O bond order, and the higher the M-C bond order. When we look at the numbers for the different carbonyls within a period we see that as expected the wavenumbers increase with increasing group number indicating a decreasing bond order. We can also look down the groups. We see that in this case, the numbers hardly change, meaning that the bond order is hardly affected by the period of the metal.
Homoleptic Carbonyls of the 8th Group (Fe, Ru, Os)
What charge-neutral carbonyls would we expect for the group 8 elements Fe, Ru, and Os?

Overall, these carbonyl need to have 18 electrons. In this case the metals have 8 electrons. The charge is 0. This means that we would have 18-8=10 electrons that would need to come from the ligand. The number of ligands needed would therefore be 10/2=5. Thus, we would expect pentacarbonyls of the composition M(CO)5 (Figure \(\PageIndex{12}\)). These carbonyls adopt the trigonal-bipyramidal shape. The group 8 carbonyls are all liquids. The iron pentacarbonyl has a light-orange color while the ruthenium and the osmium carbonyls are colorless.
Charged Trigonal-Bipyramidal Carbonyls with 18 electrons

We can again ask if there are charged isosteric pentacarbonyls with 18 e of metals other than group 8 metals. The answer is yes. The manganese is left to the iron in the periodic table and has one electron less. Therefore its pentacarbonyl needs to have a 1- charge and the composition is Mn(CO)5-. Also the higher homologues, the Tc(CO)5- and the Re(CO)5- exist. The Cr has one electron less than than the Mn, therefore its pentacarbonyl has a 2- charge and the formula is Cr(CO)52-. Mo(CO)52- and W(CO)52- are also known. The vanadium has another electron less because it is in the 5th group, therefore its pentacarbonyl has a 3- charge, and the formula is V(CO)53-. Again, the higher homologues, the Nb(CO)53- and the Ta(CO)53- are also stable. Also for the pentacarbonylates high negative charges are no problem for the stability of the complexes due to the stabilizing effect of the \(\pi\)-acceptor interactions. What about carbonyl cations with trigonal bipyramidal shape? As we go from Fe to Co, we need a 1+ charge at the carbonyl to achieve 18 electrons. The respective Co(CO)5+ cation is stable, and so are their higher homologues, the Rh(CO)5+ and the Ir(CO)5+. However, the group 10 pentacarbonyl cations Ni(CO)52+, Pd(CO)52+, and Pt(CO)52+ are not stable. The 2+ positive charge weakens the metal-carbon bond too much. This behavior is consistent with the weakening of the M-C bond with increasing positive charge due to weaker \(\pi\)-acceptor effects.
Homoleptic carbonyls of group 10 (Ni, Pd, Pt)
What about the group 10 carbonyls?

In this case the metals have 10 electrons. There is no charge. The number of ligand electrons needed is 18-10 = 8 electrons. Thus, the number of ligands is 8/2=4. Therefore, the composition is M(CO)4 (Figure \(\PageIndex{14}\)). The shape is tetrahedral because we have an 18 and not a 16 valence electron complex. Nickel tetracarbonyl is a volatile, colorless liquid. The higher homologues, the Pd(CO)4 and the Pt(CO)4 are not stable. We can explain this when remembering that the \(\pi\)-orbital overlap in tetrahedral complexes is generally weak. Therefore, the M-C carbon bond is less effectively stabilized by the \(\pi\)-acceptor interactions compared to octahedral and trigonal-bipyramidal carbonyls. This effect is even more pronounced for the Pd and Pt carbonyls because they have larger orbitals that can overlap even less effectively with the relatively small \(\pi\)*-orbitals of the CO ligand. In this case the \(\pi\)-acceptor interactions are so weak so that the entire molecule is no longer stable.
Charged Tetrahedral Carbonyls with 18 electrons

What about charged 18 electron tetrahedral carbonyls with other metals? Again, negatively charged carbonylates are stable, even with high negative charges. Co(CO)4-, Fe(CO)42-, Mn(CO)43-, and Cr(CO)44- are all stable and so are their higher homologues. The Cu(CO))4+ which has a 1+ positive charge is also known, but its higher homologues, the Ag(CO)4+ and the Au(CO)4+ are not.
Overall Stability Trends
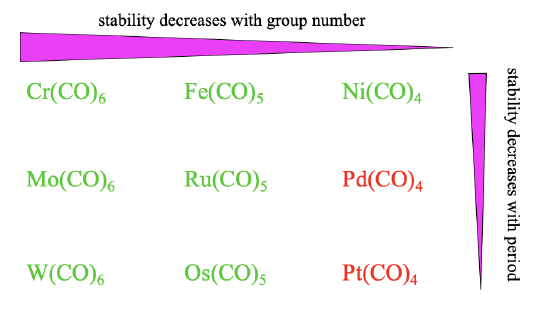
Overall the stability of carbonyls tends to decrease from group 6 to group 8 to group 10 (Figure \(\PageIndex{16}\)). This trend is because the octahedral shape allows for the best orbital overlap for \(\pi\)-acceptor interactions, followed by the trigonal bipyramidal, followed by the tetrahedral shape. The stability also tends to decline from the 4th to the 6th period. This trend can be explained by less efficient orbital overlap due to increasingly different orbital size between the ligand and the metal orbitals. These effects are sufficiently large for Pd(CO)4 and Pt(CO)4 to make them instable.
Group 4 and Group 12 Carbonyls (non-existing)
We have discussed group 6, 8, and 10 carbonyls, but not group 4 and group 12. Why? Because no carbonyls of these groups are stable. What is the reason? For group 4 carbonyls, we would need seven carbonyl ligands. This would lead to a coordination number of seven which is unacceptably high for carbonyls. For group 12 carbonyls, we would only need three carbonyl ligands. This would lead to an unacceptably low coordination number of 3.
Homoleptic carbonyls of the 7th group (M = Mn, Tc, Re)
Now let us think about what structures the homoleptic carbonyls with metals having an odd number of electrons form. Let us start with the 7th group which consists of the metals Mn, Tc, and Re. Our approach is to see how many ligands we need to produce a 17 valence electron fragment, and then dimerize that fragment.
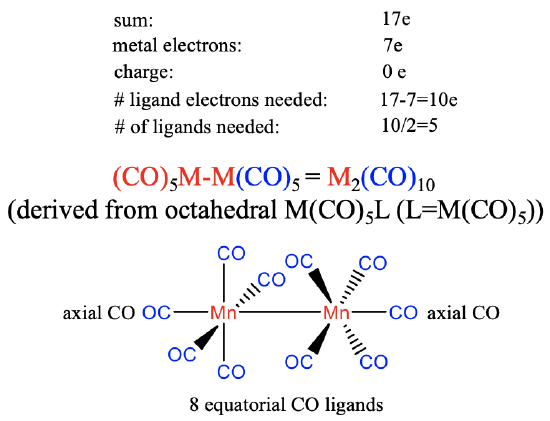
The group 7 metals have seven valence electrons. Again, we will assume that there is no charge on the carbonyl. The number of ligand electrons to produce the 17 valence electrons fragment will therefore be 17-7 = 10. The number of ligands needed is therefore 10/2=5 assuming that the carbonyl ligand is a 2-electron donor binding end-on to the metal. This gives an M(CO)5 fragment that dimerizes to form an M2(CO)10 carbonyl with a metal-metal bond. The structure can be thought to be derived from an octahedral structure in which each metal is surrounded octahedrally by five CO ligands and an M(CO)5 fragment acting as the sixth ligand. Each M(CO)5 unit has one axial ligand and four equatorial ligands, whereby the axial ligand is co-directional with the metal-metal bond. The four equatorial ligands of the first metal are in staggered conformation relative to the four equatorial ligands of the second metal due to steric repulsion arguments.
Charged Isoelectronic Carbonyls of the Type M2(CO)10
Can we make charged isoelectronic carbonyls of the type M2(CO)10 with other metals? The answer is yes, but only carbonylate anions with low negative charge, and no carbonyl cations. The formation of carbonyl cations is prohibited because of the weakening of the \(\pi\)-acceptor interactions that result from the positive charge. High negative charges are not possible because too many negative charges on the metal atoms lead to electrostatic repulsion and the destabilization of the metal-metal bonds.
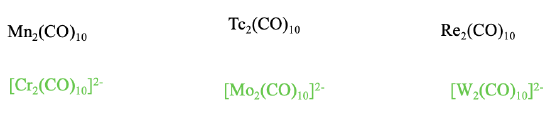
There are therefore only Cr2(CO)102-, and the higher homologues Mo2(CO)102- and W2(CO)102-, but no other M2CO10 type carbonyl ions.
Homoleptic carbonyls of the 9th group (M = Co, Rh, Ir)
What are the expected structures for the homoleptic carbonyls of group 9?
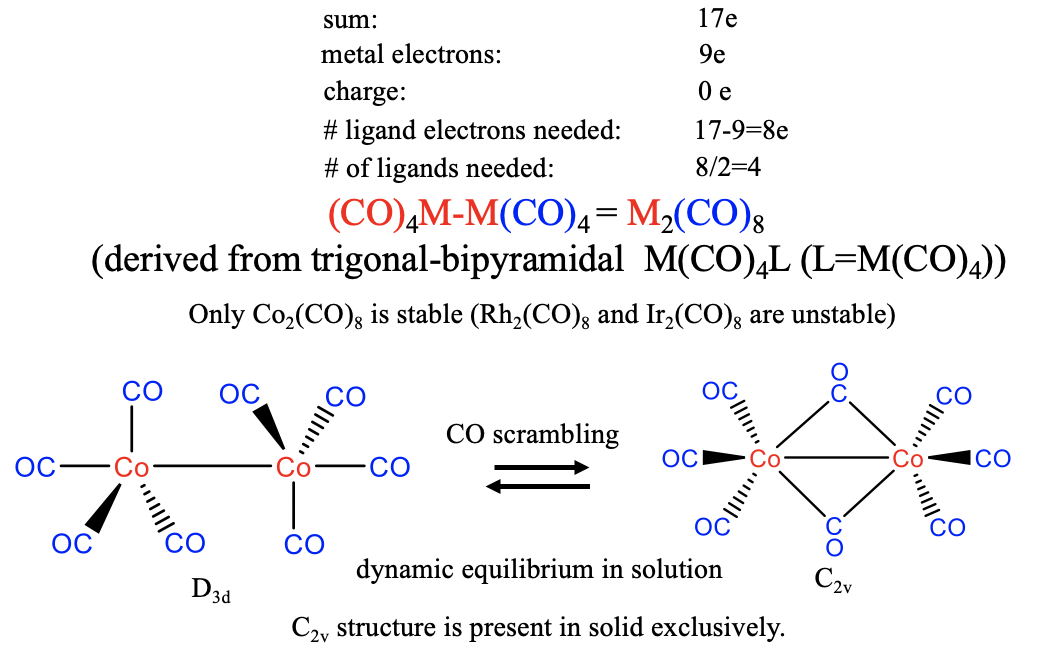
In this case, the metal contributes 9 electrons, and this means that 17-9=8 electrons need to come from the carbonyl ligand. We therefore need 8/2=4 CO molecules to produce an M(CO)4 17 valence electron fragment. Two of the fragments then dimerize to form a dinuclear carbonyl of the composition M2CO8. In nature, however, only the Co-carbonyl is realized, the Rh and the Ir analogs are unstable. The structure of the Co2(CO)8 carbonyl can be derived from an M(CO)4L trigonal-pyramid, whereby L is the second M(CO)4 unit (Fig. 10.2.19). According to that, the coordination number is 5. There are two axial and six equatorial ligands whereby the equatorial ligands are oriented in a staggered conformation. In solution this structure is in dynamic equilibrium with a second structure with C2v symmetry in which two CO ligands are bridging. Due to this equilibrium there is constant ligand scrambling, meaning that the CO ligands constantly move from axial to equatorial positions, and migrate from one metal atom to the other. In solid state the C2v-type structure is present exclusively indicating that it is slightly more stable.
Charged Isoelectronic Carbonyls of the Type M2(CO)8
The charged, isoelectronic carbonyls of the type M2(CO)8 behave similarly to that of the type M2(CO)10. There are no highly charged binuclear carbonylate anions, and no carbonyl cations.

There are only the weakly negatively charged [Fe2(CO)8]2- , [Ru2(CO)8]2-, and [Os2(CO)8]2-. The weakly negative charge stabilizes the metal-carbon bond without destabilizing the metal-metal bond too much. We can further see from this that a weakly negative charge is better for the stability of the species than no charge at all.
Homoleptic Carbonyls of the 11th Group (M = Cu, Ag, Au)
The group 11 metals Cu, Ag, and Au have eleven valence electrons.
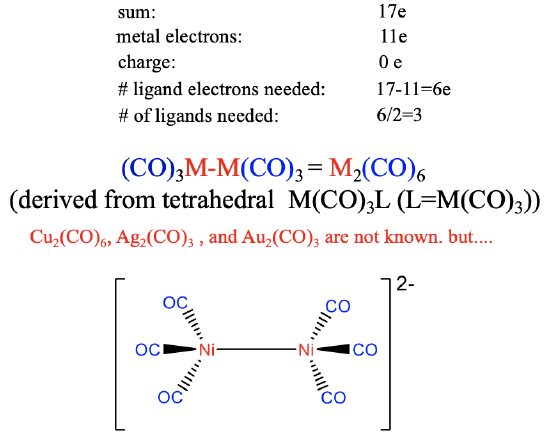
Therefore, six ligand electrons are needed to achieve 17 electrons (Figure \(\PageIndex{21}\)). This means that 6/2=3 CO ligands are required to produce the 17 valence electron fragment. The dimer of it has the composition M2(CO)6 and its structure can be derived from a tetrahedral M(CO)3L structure in which L is the second M(CO)3 fragment. Neither the Cu, nor the Ag, nor the Au carbonyl are known due to the weak \(\pi\)-overlap in tetrahedral coordination. However, the weakly negatively [Ni2(CO)6]2- ion is known which may be explained by the stabilizing effect of one negative charge on the M-C bond.
Overall Stability Trends
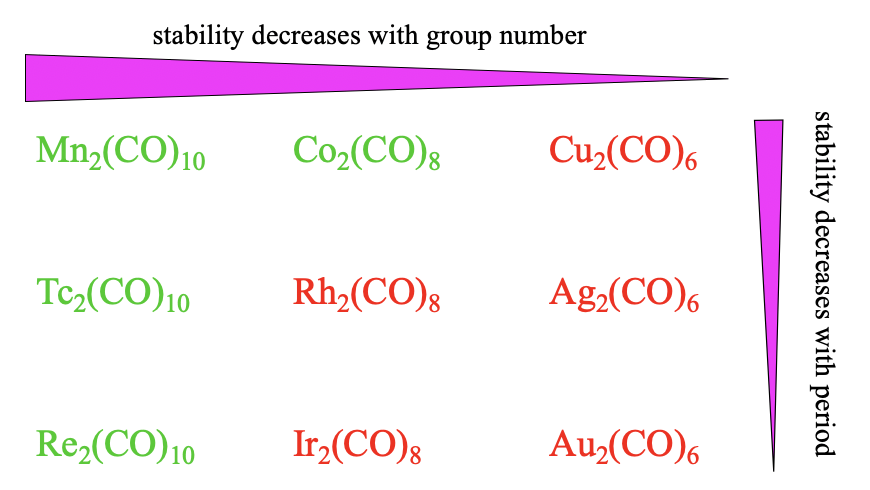
Overall, we see the same stability trends for the dinuclear carbonyls as compared to the mononuclear ones. The stability decreases with the group number because \(\pi\)-overlap becomes smaller with smaller coordination numbers. Also, we see that the stability decreases with the period because of decreasing match of orbital sizes.
Homoleptic carbonyls of the 5th group (M = V, Nb, Ta)
The 17 valence electron fragment of the carbonyl of vanadium has the composition V(CO)6. It does not dimerize because the coordination number of 6 is much more favorable compared to the coordination number 7. V(CO)6 is a dark violet radical of octahedral shape. The radical electron is sterically inactive. V(CO)6 can be used as an oxidant because it can be reduced easily to the 18 valence electron species V(CO)6-. The higher homologues Nb(CO)6 and Ta(CO)6 are not known. This may be explained by the weaker orbital overlap between the relatively small \(\pi\)*-orbitals of the carbonyl ligand and the large metal d-orbitals of Nb and Ta.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.
Synthesis
Metal carbonyl complexes containing only CO ligands abound, but most cannot be synthesized by the method we all wish worked, bathing the elemental metal in an atmosphere of carbon monoxide (entropy is a problem, as we already discussed for W(CO)6). This method does work for nickel(0) and iron(0) carbonyls, however.
M + n CO → M(CO)n [M = Fe, n = 5; M = Ni, n = 4]
Other metal carbonyl complexes can be prepared by reductive carbonylation, the treatment of a high-oxidation-state complex with CO. These methods usually require significant heat and pressure. One example:
WCl6 + CO + heat, pressure → W(CO)6
Still other methods employ deinsertion from organic carbonyl compounds like dimethylformamide. These methods are particularly useful for preparing mixed carbonyl complexes in the presence of reducing ligands like phosphines.
IrCl3(H2O)3 + 3 PPh3 + HCONMe2 + PhNH2 → IrCl(CO)(PPh3)2 + (Me2NH2)Cl + OPPh3 + (PhNH3)Cl + 2 H2O
The key thing to notice about the reaction above is that the CO ligand is derived from dimethylformamide (DMF).


