12.6.1: Kinetics and Stereochemistry of Square Planar Reactions

Kinetics

In general, the reaction kinetics of square-planar associative substitution takes the form of the following rate law, which has two terms:

\[\frac {d \ce{[ML3Y]}}{dT} =k_1 \ce{[ML3X]} + k_2 \ce{[ML3X][Y]} \nonumber \]

Each of the terms corresponds to one of the two possible reaction pathways. The term, \(k_2 \ce{[ML3X][Y]}\), is second-order, and corresponds to a simple associative pathway. The \( k_1 \ce{[ML3X]}\) term is first-order, although it also corresponds to an associative pathway. The reason it appears to be first order is because square planar complexes can react through a solvent-assisted pathway where bulk solvent replaces the leaving group, and then is replaced by the entering group (Figure \(\PageIndex{2}\)). Because solvent concentration does not appreciably change as the reaction proceeds, it is not part of the rate law term even though it is involved in the rate-determining association. The step in which solvent is substituted by the entering group must happen faster than the solvent-assisted replacement of X.

Figure \(\PageIndex{2}\): Solvent-assisted substitution pathway where X is the leaving group, Y is the entering group, and S is solvent. (CC-BY-SA; Kathryn Haas)

The kinetic rate constats in square planar substitution can depend on the identities of the leaving group, the ligand trans to the leaving group, and the entering group. The ligands that are in the \(cis\) positions with respect to the leaving group do not have a significant affect on the rate, and these are referred to as spectator ligands.

Stereochemistry

Square planar complexes react to give products in which the stereochemistry of the reactant is retained. In other words, a trans-reactant will give a trans-product, and a cis-reactant will give a cis-product (Figure \(\PageIndex{3}\)). The identity of the trans ligand has particular importance in the outcome of square planar substitutions (discussed further in the next sections). We will designate the trans ligand generally with the symbol T to indicate its position (Figure \(\PageIndex{3}\)), the leaving group as X, and the entering group as Y. The spectator ligands (ligands that are \(cis\) to X) will be desginated L and L'. For the discussion that follows, the plane of the metal complex will be designated as the \(xy\) plane, while the \(z\) axis is perpendicular to the plane (Figure \(\PageIndex{3}\)). The \(x\) and \(y\) axes will run colinear to the bond axes, with the \(x\) axis running colinear to the T-M-X bonds (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): Stereochemistry is strictly retained in the reactions of square planar complexes. By convention, the plane of the metal complex is the \(xy\) plane, with the \(x\) axis colinear with the T-M-X bonds. M = metal ion | X = leaving group ligand | Y = entering group ligand | T = ligand trans to the leaving/entering group. (CC-BY-SA; Kathryn Haas)

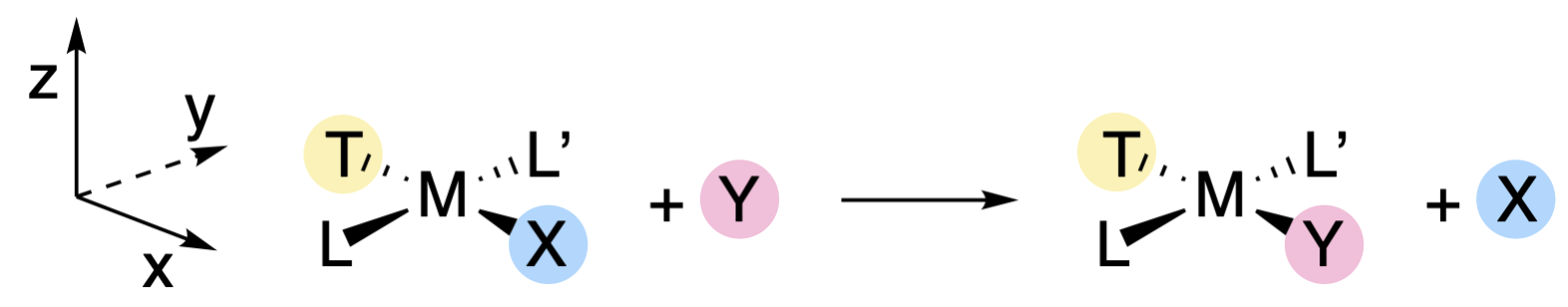
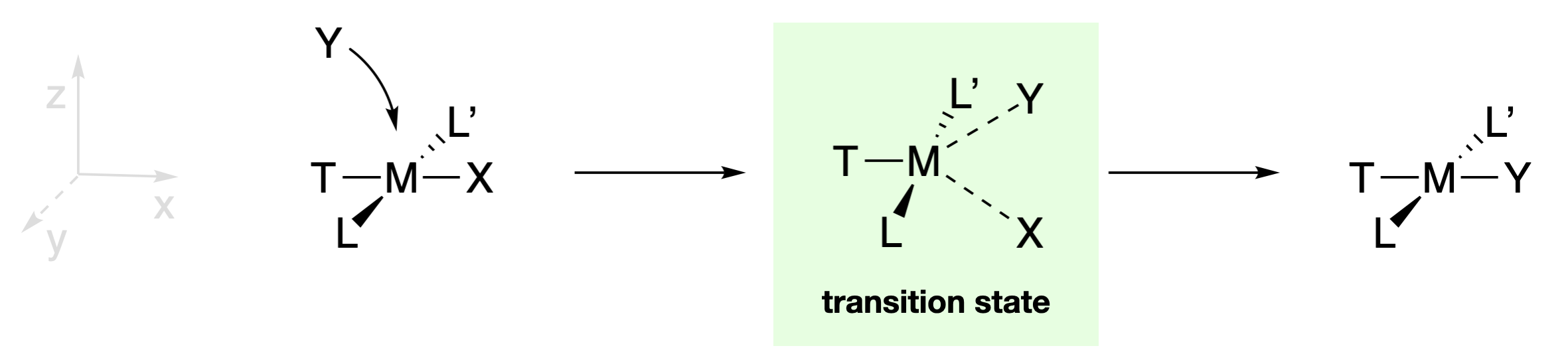
The retention of stereochemistry, and the fact that X, Y, and T can influence the rate of reaction provide hints at the nature of intermediates and/or transition states involved in these reactions. The existence of five-coordinate square pyramidal structures, like those of \(\ce{[Ni(CN)5]^3-}\) and \(\ce{[Pt(SnCl3)5]^3-}\), suggests that five-coordinate intermediates are possible. However the substitutions of square planar complexes are generally classified as associative interchange mechanisms (\(I_a\)) because isolation of a true intermediate is rarely accomplished. In any case, the retention of stereochemistry is explained by a five-coordinate trigonal bipyramidal transition state in which X, Y, and T are each in the trigonal plane (along with the metal center). As the M-X bond is breaking, the M-Y bond is forming and Y replaces X in the position trans to T. Because T, Y and X are in the trigonal plane in the transition state, all three ligands are able to interact with the same \(d\) orbitals of the central metal ion. Thus the identities of X, Y, and T should influence the ability of the M-X bond to break and the M-Y bond to form. On the other hand, L and L' are in a perpendicular plane, and would interact with different orbitals than X and Y. This explains why spectator ligands L and L' have little effect on the reaction rate, as they are interacting with different orbitals than those involved in bond breaking and bond making.

Figure \(\PageIndex{4}\): Mechanism for simple \(I_a\) substitution. The structure of the transition state is trigonal bipyramidal, with T, X, and Y in the trigonal plane with M. The spectator ligands, L and L', are in a perpendicular plane and are coplanar with T and M. (CC-BY-SA; Kathryn Haas)

The solvent-assisted pathway can occur through similar transition states and mechanistic steps, except that there are additional steps involving solvent association and displacement.

Figure \(\PageIndex{5}\): Solvent-assisted \(I_a\) substitution. Compare to Figure \(\PageIndex{4}\). S is solvent. (CC-BY-SA; Kathryn Haas)

Although there is general consensus that square planar complexes react through associative pathways, the characterization of intermediates and/or transition states has remained elusive, and there is still debate as to the intricate details of the reaction mechanisms involving square planar complexes. For example, there are arguments that a six-coordinate transition state may exist in the solvent-assistant pathway.