12.5.1: Substitution in trans-en octahedral complexes

Last updated
Save as PDF

Page ID: 389966

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The reaction of metal complexes of the form \(\ce{[M(en)2LX]^{n+}}\) have multiple possible pathways in terms of the structure of the intermediate.

When the X ligand departs from a trans complex, the most likely case is that the L ligand will remain in the axial position. In that case, there is one primary structure for the square pyramidal intermediate. Reaction of that intermediate with the incoming ligand, Y, will result in retention of trans stereochemistry.

An alternative possibility is that the intermediate adopts a trigonal bipyramidal structure. In that case, the outcome of the reaction depends on which of the possible trigonal bipyramidal structures exist and their relative amounts. There are two chemically distinguishable positions on the trigonal bipyramid; the axial and equatorial positions. The remaining L ligand can occupy either the axial position, which has a slightly longer bond, or the equatorial positions, which are slightly closer to the metal and more sterically hindered in space. To adopt either of the trigonal bipyramidal structures, rearrangement of the complex is necessary. It is more likely that the rearrangement will result in the trans ligand being in the equatorial position, since that requires less distortion of the original positions of each ligand (this is not obvious from the structures in Figure \(\PageIndex{1}\)). A trigonal structure with axial L requores one of the en ligand nitrogens to move by 90 degrees, while a structure with equitoral L requires only 30 degree movement from any ligand. As a result, the trigonal bipyramid with equitorial L (bottom of Figure \(\PageIndex{1}\)) is the dominant trigonal bipyramidal structure. That structure can produce three optical isomers from the three different angles of ligand Y entering along the equitorial plane. When Y enters trans to L, it produces the trans product. When Y enters cis to L, it produces either of the two cis optical isomers. The cis-\(\Lamda\) and \(cis-\Delta\) isomers are equally likely, and are produced as a racemic miture from an optically inactive starting trans reactant. The expected ratios of cis to trans are 2:1.

Regarding the trigonal bipyramidal intermediates, the identity of L influences its preference for the axial or equatorial positions. For example, \(\pi\)-donor ligands prefer equatorial positions due to the shorter bond lengths involved in \(\pi\)-donor interactions. Thus, when L is a strong \(\pi\)-donor, reaction products are more likely to come from the trigonal intermediate with an equatorial L. This last point is relevant to reactions where the conjugate base mechanisms is at play. The deprotonated ligand that results from the conjugate base mechanism is a stronger \(\pi\)-donor, and has preference for occupation of the equatorial positions of a trigonal bipyramidal intermediate. Even in cases where the square pyramid is typically preferred, the conjugate base mechanism can result in preference for a trigonal intermediate.

possible intermediates and rxt outcomes for trans_en octahedron.png — Figure \(\PageIndex{1}\): Three different possibilities for the five-coordinate intermediate yield different possibilities for the stereochemistry of the product complex. The possibility of a square pyramid with basal ligand is not shown and is considered less likely than the three pathways shown because it would require a long-lived intermediate to allow time for the rearrangement of the square planar intermediate shown. (CC-BY-SA; Kathryn Haas)

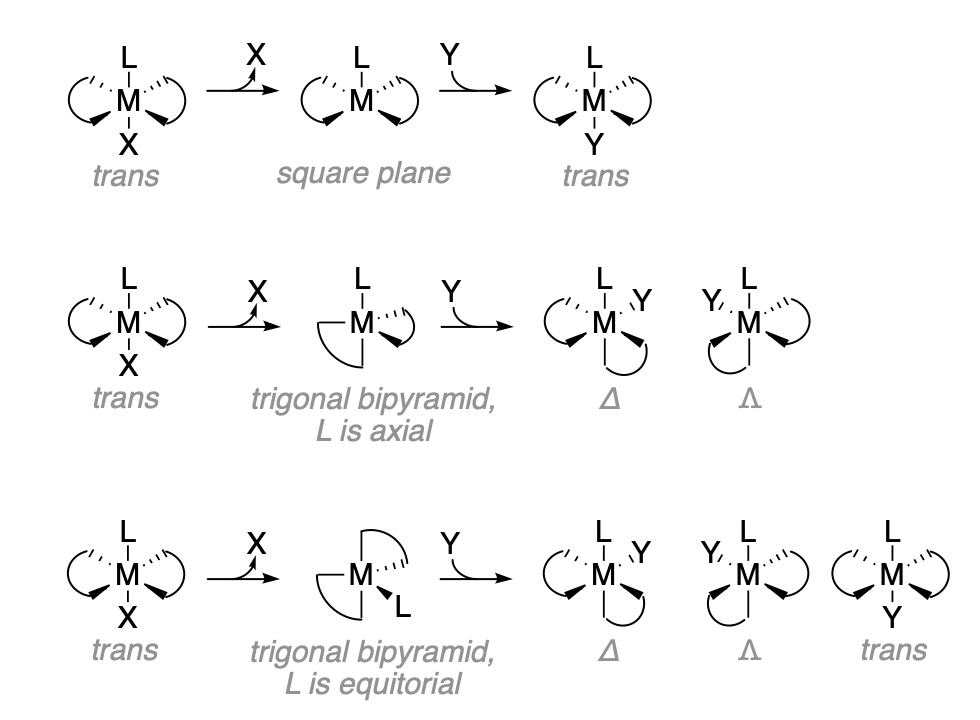
The actual proportion of reaction products of a given stereochemistry depends on the extent to which each of the possible intermediates leads to the products. However, the expected percentages of cis-trans from any single intermediate is rarely found in experimental data (See Table \(\PageIndex{1}\)).

Table \(\PageIndex{1}\) gives the % of trans stereochemistry retained in the displacement of \(\ce{Cl^-}\) by either \(\ce{H2O}\) or \(\ce{OH^-}\)in a series of \(\ce{trans-[Co(en)2LCl]^+}\) complexes where the identity of the trans ligand, \(\ce{L^-}\), is varied.

The reactions run under acidic conditions is shown below, and its data is shown in the middle column in Table \(\PageIndex{1}\) :

\[\ce{trans-[Co(en)2LCl]^+ + H2O <==> [Co(en)2L(H2O)]^2+ + Cl^-} \nonumber \]

The reactions run under basic conditions is shown below, and its data is shown in the right column in Table \(\PageIndex{1}\) :

\[\ce{trans-[Co(en)2LCl]^+ + OH^- <==> [Co(en)2L(OH)]^+ + Cl^-} \nonumber \]

Table \(\PageIndex{1}\): % trans product under different conditions
\(\ce{L^-}\)	% trans product under acidic conditions (stereochemistry of reactant is retained)	% trans product under basic conditions (stereochemistry of reactant is retained)
\(\ce{OH^-}\)	25	6
\(\ce{NCS^-}\)	30-50	24
\(\ce{Br^-}\)	50	100
\(\ce{Cl^-}\)	65	95
\(\ce{NH3^-}\)	100	24
\(\ce{NO2^-}\)	100	94
Data from Miessler, G. L.; Fischer, P. J.; Tarr, D. A. Inorganic Chemistry, 5th Ed. Pearson: Boston, 2014, p. 459.