12.3.1: Rate Law for Dissociative Mechanisms
- Page ID
- 385511
Derrivation of the Rate Law
A Dissociative (D) mechanism is two steps in which the first step is the dissociation of a ligand. The intermediate, \(\color{blue}{\ce{ML_{n}}}\), has a lower coordination number than that of the reactant, \(\ce{ML_{n}X}\).
\[\begin{array}{rc}
\text{Step 1 (Dissociation):} & \ce{ML_{n}X <=>[k_1][k_{-1}]}\textcolor{blue}{\ce{ML_{n}}}\ce{ + X}\\
\text{Step 2 (Association):} & \textcolor{blue}{\ce{ML_{n}}}\ce{ + Y <=>[k_2][k_{-2}] ML_{n}Y} \\
\hline \text{Overall Reaction:} & \ce{ML_{n}X + Y <=> ML_{n}Y + X}
\end{array} \nonumber \]
If we assume that \(k_{-2}<<k_2\), the rate law for the formation of products is the rate law of the second step.
\[\frac{d\left[\mathrm{ML}_{n}\right]}{d t}=k_{2} \textcolor{blue}{\ce{[ML_{n}]}} \ce{[Y]} \nonumber \]
We can assume that the concentration of the intermediate is small enough that it would be difficult or impossible to measure its concentration. Here, we can evoke the steady-state approximation and assume that the concentration, \(\color{blue}{\ce{[ML_{n}]}}\), is approximately unchanging over the course of reaction. The \(\color{blue}{\ce{[ML_{n}]}}\) depends on \(k_1, k_{-1}\) and \(k_2\). These assumption are expressed mathematically as follows.
\[\frac{d\left[\mathrm{ML}_{n}\right]}{d t}=k_{1}\left[\mathrm{ML}_{n} \mathrm{X}\right]-k_{-1}\left[\mathrm{ML}_{n}\right][\mathrm{X}]-k_{2}\left[\mathrm{ML}_{n}\right][\mathrm{Y}]=0 \nonumber \]
We can then use the equation above to solve for \(\color{blue}{\ce{[ML_{n}]}}\).
\[\textcolor{blue}{\ce{ML_{n}}}=\frac{k_{1}\left[\mathrm{ML}_{n} \mathrm{X}\right]}{k_{-1}[\mathrm{X}]+k_{2}[\mathrm{Y}]} \nonumber \]
Then substitution this into the rate law given above for the second step of the mechanism. This would yield a rate law that depends only on species with measurable concentrations.
\[\frac{d\left[\mathrm{ML}_{n} \mathrm{Y}\right]}{d t}=\frac{k_{2} k_{1}\left[\mathrm{ML}_{n} \mathrm{X}\right][\mathrm{Y}]}{k_{-1}[\mathrm{X}]+k_{2}[\mathrm{Y}]} \nonumber \]
The rate law above suggests that the rate of product formation has an inverse relationship to the concentration of the outgoing ligand, X. This is one piece of evidence that can be used to distinguish a Dissociative mechanism; that is if the rate of reaction decreases as [X] in solution is increased it is evidence of a D mechanism. This rate law also suggests that ther is a complicated dependence of the reaction rate on the concentration of incoming ligand, Y. The importance of [Y] compared to [X] depends mathmatically on the weight of the two values in the demoninator of the rate law. If [X] >> [Y], then a valid approximation is to assume that the \(k_2\ce{[Y]}\) term is relatively small and simplify the rate law by dropping it out completely.
\[\text{If X >> Y, then simplify: } \frac{d\left[\mathrm{ML}_{n} \mathrm{Y}\right]}{d t}=\frac{k_{2} k_{1}\left[\mathrm{ML}_{n} \mathrm{X}\right][\mathrm{Y}]}{k_{-1}[\mathrm{X}]} \nonumber \]
The resulting rate law (above) has a simpler dependence on [Y]; that is when [X] is large, the reaction rate is directly related to [Y].
The opposite extreme is under conditions of high [Y]. This yields a rate law that is first order in its dependence on the reactant metal complex. When [Y] is large, and the \(k_{-1}\ce{[X]}\) term is relatively insignificant, the rate law can be simplified to the pseudo-first order rate law as follows.
\[\text{If Y >> X, then simplify: } \frac{d\left[\mathrm{ML}_{n} \mathrm{Y}\right]}{d t}= k_{1}\ce{[ML_{n}X]} \nonumber \]
The best type of experimental evidence to determine a dissociative mechanism would be a systematic study of the dependence of rate on both [X] and [Y]. However, the dissociative reaction is unique in that it displays this type of saturation kinetics at high concnetration of the incoming ligand, and so the study of how a reaction rate behaves under high [Y] is common.
First-order reactions
Under conditions of high [Y], the a reaction following a D mechanism is said to follow "first order" kinetics. This type of reaction is sometimes called a first order reaction. That means the rate law depends on only one concentration term.
Why does the dissociative mechanism depend on concentrations in this specific way?
The rate depends on one molecule losing a ligand. Once it does so, a second ligand can replace the one that left. However, losing a ligand may be harder to do than gaining a new one. To lose a ligand, a bond must be broken, which costs energy. To gain a new ligand, a bond is made, releasing energy. That first step is harder to do, so it takes longer. It is a bottleneck that slows the reaction down. It is called the rate-determining step.
- The rate-determining step is the slow step of the reaction.
- The rate-determining step controls the rate of the overall reaction; everything else has to wait for that step to happen.
- Once the rate-determining step has occurred, everything else follows very quickly.
No collision is necessary for the metal complex to lose a ligand. Instead, a bond in the metal complex has to break. That just takes time and energy. As a result, concentration of the incoming ligand matters very little.
We should think a little more about energy requirements, available energy and reaction rate. It takes a certain amount of energy to break a bond. Over any given period of time, a specific amount of energy is available in the surroundings to use. That energy is not available uniformly. Some molecules will get more energy from their surroundings and others will get less. There will be a statistical distribution, like a bell curve, of energy available in different molecules. That means bond-breaking events are governed by statistics.
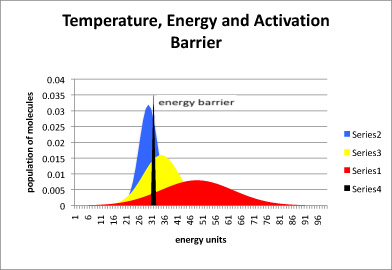
Figure \(\PageIndex{2}\): The relationship between temperature, energy available, and energy barrier. The black line represents energy needed to start the reaction, also called the energy barrier or the activation barrier. The blue curve is the distribution of available energy in a group of molecules at a cooler temperature. The yellow curve is for a group of molecules that is a little warmer, and the red curve even warmer.
In figure \(\PageIndex{2}\), most of the molecules at the low temperature (blue) do not have enough energy to begin the reaction. A small portion do, and so the reaction will proceed, but very slowly. In the yellow curve, there is more energy available, and so a large fraction of molecules have the energy necessary to begin the reaction. In the red curve, the vast majority have sufficient energy to react. Thus, one of the factors governing how quickly a reaction will happen is the energy needed, or activation barrier. A second factor is the energy available, as indicated by the temperature.
Of course, even if there is enough energy for the reaction, the reaction might not occur yet. Energy is necessary but not sufficient to start a reaction. There are also statistical factors in terms of whether a molecule has its energy allotted into the right places, or in some cases, whether two molecules that need to react together are oriented properly.
Suppose at a given temperature it takes a specific amount of time for half the molecules to gain enough energy so that they can undergo the reaction. That amount of time is called the half life of the reaction. After one half life, half the molecules have reacted and half remain. After a second half life, half the remaining molecules (another quarter, for three quarters of the original material in all) have also reacted, and a quarter still remain. After a third half life, half the remaining ones (another eighth, making it seven eighths reacted in total) will have reacted, leaving an eighth of the original material behind.
- Exponential decay is based on a statistical distribution of energy availability.
- The concept of half life is related to exponential decay.
- It takes a fixed period of time for a half of the metal complex obtain enough energy to dissociate.
Thus, the time it takes for the reaction to happen does not really depend on the concentration of anything.
However, the change in concentration over time -- the quantity that we can usually measure most easily -- depends on the original concentration, and for that reason the concentration of the metal complex appears in the rate law.
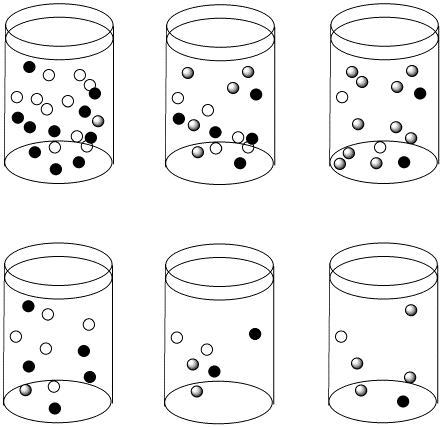
Figure \(\PageIndex{3}\): The reactions in the top row and bottom row are proceeding with the same half-life as we move from left to right. However, the top row starts out more concentrated than the bottom row. As a result, the concentrations in the top row are changing more quickly than in the bottom row.
Suppose the half life for a particular case of ligand substitution is one second. After a half life, a 1 M solution becomes 0.5 M, so the rate of change in concentration per time is 0.5M/s. But after the same half life, a 0.5 M solution becomes 0.25 M, so the change in concentration is 0.25 M/s.
If a first order reaction has a half-life of 120 seconds, how much of the original material is left after
a) four minutes? b) six minutes? c) eight minutes? d) ten minutes?
- Answer a
-
4 minutes = 240 seconds = 2 x 120 second = 2 half lives.
Material left = 50% x 50% = 0.5 x 0.5 = 0.25 = 25% left
- Answer b
-
6 minutes = 360 seconds = 3 x 120 second = 3 half lives.
Material left = 0.5 x 0.5 x 0.5 = 0.125 = 12.5% left
- Answer c
-
8 minutes = 480 seconds = 4 x 120 second = 4 half lives.
Material left = 0.5 x 0.5 x 0.5 x 0.5 = 0.0625 = 6.25% left
- Answer d
-
10 minutes = 600 seconds = 5 x 120 second = 5 half lives.
Material left = 0.5 x 0.5 x 0.5 x 0.5 x 0.5 = 0.03125 = 3.125% left
Given the first-order dissociative rate law above, what would happen to the reaction rate for substitution in each of the following cases?
- the concentration of ligand is doubled, and the concentration of metal complex is doubled
- the concentration of ligand is tripled, and the concentration of metal complex is halved
- the concentration of ligand is doubled, and the concentration of metal complex is tripled
- the concentration of ligand is halved, and the concentration of metal complex is halved
- Answer a
-
Dissociative Rate Law: Rate = [MLn], if MLn is the complex. There is no dependence on [X], if X is the new ligand.
Rate will double: Rate = 2 x [MLn]0, if [MLn]0 is the original concentration.
- Answer b
-
Rate will be halved: Rate = 0.5 x [MLn]0.
- Answer c
-
Rate will triple: Rate = 3 x [MLn]0.
- Answer d
-
Rate will be halved: Rate = 0.5 x [MLn]0.
Plot graphs of initial rate vs concentration to show what you would see in dissociative substitution.
a) The concentration of metal complex, [MLn], is held constant at 0.1 mol/L and the concentration of ligand is changed from 0.5 mol/L to 1 mol/L and then to 1.5 mol/L.
b) The concentration of new ligand, [X], is held constant at 0.1 mol/L and the concentration of metal complex is changed from 0.5 mol/L to 1 mol/L and then to 1.5 mol/L
Given the following sets of initial rate data, determine whether each case represents a dissociative substitution. [MLn] = concentration of the coordination complex; [X] = concentration of incoming ligand.
a)
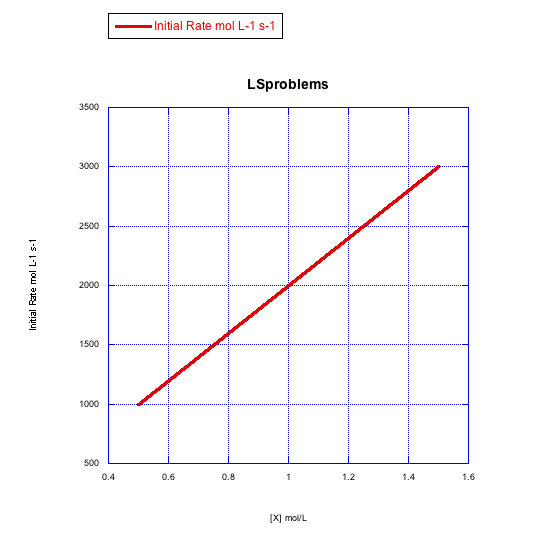
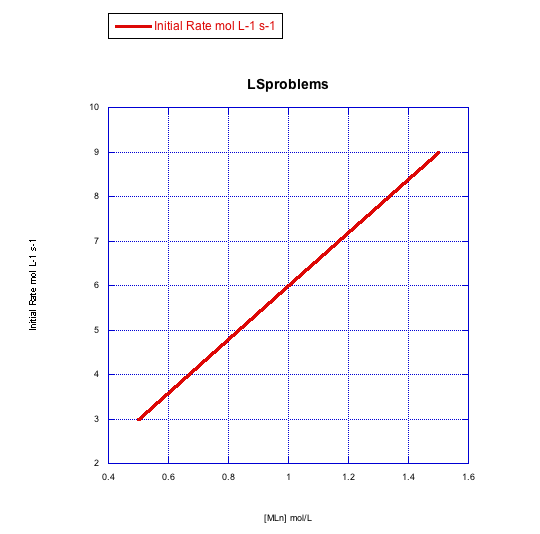
b)
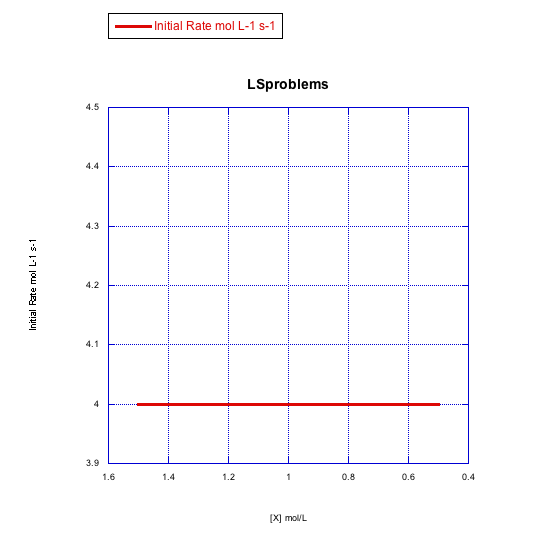
Answer a-
The rate increases with both concentration of metal complex and incoming ligand. This looks like an associative mechanism.
- Answer b
-
The rate depends on concentration of the metal complex, but not the incoming ligand. This looks like a dissociative mechanism.
- Answer c
-
The rate depends on the concentration of incoming ligand, but not the metal complex. Whatever is going on here, it isn't a simple dissociative mechanism.
In the following data, the concentration of the metal complex and the incoming ligand were held constant, but more of the departing ligand was added to the solution.
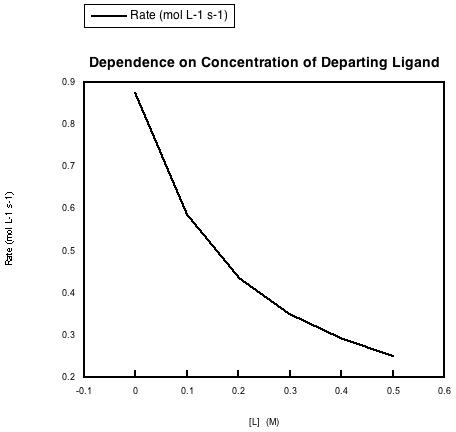
a) Explain what the data says about rate dependence on this concentration.
b) Explain this rate dependence in terms of the reaction.
- Answer a
-
The rate of the reaction is depressed when the concentration of the departing ligand is increased.
- Answer b
-
This dependence could indicate an equilibrium in the dissociative step. The more departing ligand is added, the more the equilibrium is pushed back towards the original metal complex. With less dissociated metal complex around, the entering ligand cannot form the new complex as quickly.
In certain solvents, such as THF, acetonitrile and pyridine, the rate law for substitution often appears to be Rate = k1[MLn] + k2[MLn][X], in which X is the incoming ligand and MLn is the metal complex.
a) What do these solvents have in common?
b) What is a possible explanation for this rate law?
c) This rate law has been shown to be consistent with an entirely associative mechanism. How is that possible?
- Answer a
-
These solvents all have lone pairs. They could be Lewis bases or nucleophiles.
- Answer b
-
It looks like two competing mechanisms. On term suggests a dissociative mechanism, whereas the other term suggests a dissociative mechanism. They could be happening in competition with each other.
- Answer c
-
On the other hand, it could be that there is one mechanism with two different nucleophiles. If the incoming ligand is the nucleophile, the term on the right shows up in the rate law. If the solvent is the nucleophile, forming a third complex, the term on the left shows up in the rate law. That's because we would typically change the amount of metal complex and the amount of ligand that we add to the solution in order to determine the rate law, but we wouldn't normally be able to change the concentration of the solvent, so it would be a constant. (How could you confirm this explanation in an experiment?)