Skip to main content
Chemistry LibreTexts

12.1: Introduction to Reactions of Metal Complexes

  1. Last updated
  2. Save as PDF
  • Page ID
    385527

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Although there are a vast array of reactions that occur at transition metal centers, we will touch on only a subset of the possibilities. This chapter will focus on the reactions of octahedral and square planar metal complexes, and the reactions will be divided into three types:

    1. Substitution reactions at the metal center: these are reactions in which one ligand is replaced with another ligand within the metal's inner coordination sphere.
    2. Redox: these are reactions in which the metal oxidation state formally changes by gaining or loosing electrons.
    3. Ligand reactions: these are reactions that occur primarily on the ligands that are bound to metal ions.

    Review of reaction coordinate diagrams and terms

    Before we begin our discussion of reactions, let's review some of the vocabulary and models that chemists use to understand reactions.

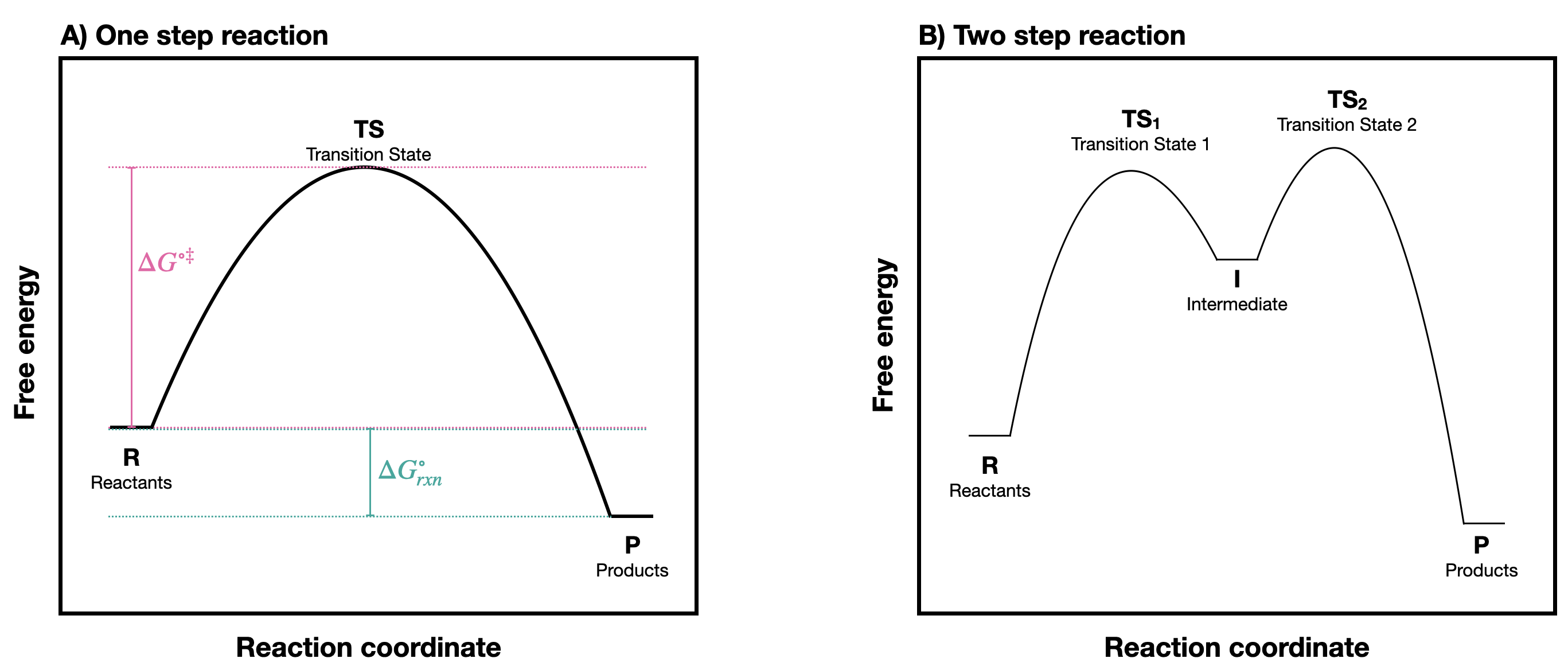
    A chemical reaction can be represented with a reaction coordinate diagram in which the total potential energy of a state is plotted in the vertical \(y\) axis, and the "reaction coordinate" (sometimes also referred to as "reaction progress", or "extent of reaction") is plotted on the horizontal \(x\) axis. The reaction coordinate is often drawn as the progress of a reaction from reactants (R) on the left to products (P) on the right.* Examples of reaction coordinate diagrams for a one-step and a two-step reaction are shown in Figure \(\PageIndex{1}\). Notice the difference in the reaction profile that depends on the number of reaction steps. A one-step reaction has one "hill" shape, while a two step reaction takes on a "saddle" shape.

    clipboard_e491e03fd4742ed70c5318f9e0e1ed7e2.png
    Figure \(\PageIndex{1}\): Examples of a reaction coordinate diagram for a one-step reaction (left), and a two-step reaction (right). (CC-BY-SA; Kathryn Haas)
    *Many students find it helpful to envision the horizontal axis in an reaction coordinate diagram as being analogous to the progress bar at the bottom of a youtube video.

    Thermodynamics

    The difference in energy between reactants (R) and products (P) indicates whether reactants or products will dominate at thermodynamic equilibrium. At standard conditions, this difference is the standard Gibbs Free Energy of the reaction (\(\Delta G^{\circ}_{rxn}\) or \(\Delta G^{\circ}\)). The Gibbs free-energy change is a combination of enthalpy change (\(\Delta H^{\circ}\)) and entropy change (\(\Delta S^{\circ}\)):

    \[\Delta G^{\circ} = \Delta H^o - T\Delta S^o \nonumber \]

    where

    • \(T\) is the temperature in Kelvin (recall that the Kelvin temperature is simply the Celsius temperature plus 273.15).
    • Enthalpy change (\(\Delta H^{\circ}\)) is the heat released or absorbed by the reaction.
    • Entropy change (\(\Delta S^{\circ}\)) is the change in disorder from reactants to products. In a reaction in which one molecule cleaves into two smaller molecules, for example, disorder increases, so \(\Delta S^{\circ}\) is positive.

    The standard Gibbs free energy change for a reaction can be related to the reaction's equilibrium constant \(K_{eq}\) by the equation:

    \[\Delta G^{\circ} = -RT \ln K_{eq} \nonumber \]

    where \(R\) is the gas constant (8.314 J/mol×K) and \(T\) is the temperature in Kelvin (K).

    A negative value for \(\ce{\Delta G_{rnx}^{\circ}}\) (an exergonic reaction) corresponds to \(\ce{K_{eq}}\) being greater than 1, an equilibrium constant which favors product formation. Conversely, an endergonic reaction has a positive value of \(\ce{\Delta G ^{\circ}}\), and a \(\ce{K_{eq}}\) between 0 and 1.

    Kinetics

    The highest point between two energy minima is a transition state (TS). The difference in energies of the reactant and the highest-energy TS is the standard free energy of activation (\(\ce{\Delta G^{\circ \ddagger}}\)). The activation energy, in combination with the temperature at which the reaction is being run, determines the rate of a reaction: the higher the activation energy, the slower the reaction. The rate constant (\(k\)) is the proportionality constant relating the rate of the reaction to the concentrations of reactants. The relationship between activation energy and the rate constant, \(k\), is given by the Arrhenius equation:
    \[k = Ae^{-\frac{E_a}{RT}} \quad \quad \text{or} \quad \quad \ln k=\ln A-\frac{E_{A}}{R T} \nonumber \]

    A rate law is an expression showing the relationship of the reaction rate to the concentrations of each reactant. The rate is defined as the change in reactants or products over time. For example, in a reaction of two reactants (\(R_1\) and \(R_2\)) to form product (P), a rate law could be written as follows:
    \[\frac{d\ce{[P]}}{dT}=\ce{k[R_1][R_2]} \nonumber \]
    The rate law above is second order overall, and first order with respect to both \(R_1\) and \(R_2\). The order indcates the power of reactant concentrations for individual reactants or overall for the reaction.

    In a one-step reaction, the product is formed in one step. There is an energy barrier to overcome so that this process can happen. At the height of that energy barrier is the TS. In a one-step reaction, there is one transition state. In contrast, in a two-step reaction, there are two transition states and an intermediate (denoted by the letter I). The first step from R to I, passes over transition state \(TS_1\), is endergonic. The second step passing through transition state \(TS_2\) is exergonic. The intermediate (I) is thus depicted as an energy 'valley' (a local energy minimum) situated between the two energy maxima; \(TS_1\) and \(TS_2\).

    In Figure \(\PageIndex{1}\)B, notice that the energy barrier for the first step is larger than the energy barrier for the second step. This means that the first step is slower than the second. In a multi-step reaction, the slowest step - the step with the largest energy barrier - is referred to as the rate-limiting or rate-determining step. The rate-determining step can be thought of as the 'bottleneck' of the reaction: a factor which affects the rate-determining step will affect the overall rate of the reaction. Conversely, a factor which affects only a much faster step will not significantly affect the rate of the overall reaction.

    Summary and Key Terms

    Reaction coordinate diagrams convey some very important ideas about how the reaction can proceed, and about the thermodynamics and kinetics of the reaction. In the sections that follow, the following key terms will be used:

    Description of Key Terms

    Reactants (R): The molecular species that are the starting materials for a chemical reaction. These are often written at the left side of a reaction coordinate diagram.

    Products (P): The molecular species that result from a chemical reaction. These are often written at the right side of a reaction coordinate diagram.

    Transition State (TS): a transition state is the transient species that exists at an energy maximum. In other words, TS's are highest-energy structures along a reaction pathway. Hammond's postulate suggests that the structure of a transition state should resemble the lower-energy species (R, P, or I) adjacent to it along the reaction coordinate, and most closely resembles the structure of the species closest in energy.

    Intermediate (I): an intermediate is a high-energy structure at a local minimum. Intermediates are sometimes thought of as long-lived transition states. Unlike transition states, intermediates sometimes exist long enough and in high enough concentration to be detectable experimentally.

    Microscopic reversibility: if a reaction can proceed in the forward direction from R to P, then in principle, it can also proceed in the reverse direction from P to R. There may be many possibilities for how a reaction could happen, but the lowest-energy pathway in the forward direction is also the lowest energy pathway in the reverse direction. In other words, the reactions passes through the same lowest-energy I and TS in the forward and reverse directions.

    Steady-State Approximation: the concentration of an intermediate is assumed to react as quickly as it forms. This approximation allows us to assume that concentration of an intermediate remains "steady" throughout the reaction progress. This approximation is useful for analysis of reaction kinetics.

    Order: The order of a reaction indicates the power of total reactant concentration in a kinetic rate law. The order of a reactant indicates that reactant's power in the rate law. For example, is a rate law that is \(\ce{Rate = k [A]^2[B]}\), the reaction is second order in A, first order in B and third order overall. If there were also a reactant, C, that was not part of the rate law, the reaction would be zero order with respect to C.

    Exercise \(\PageIndex{1}\)

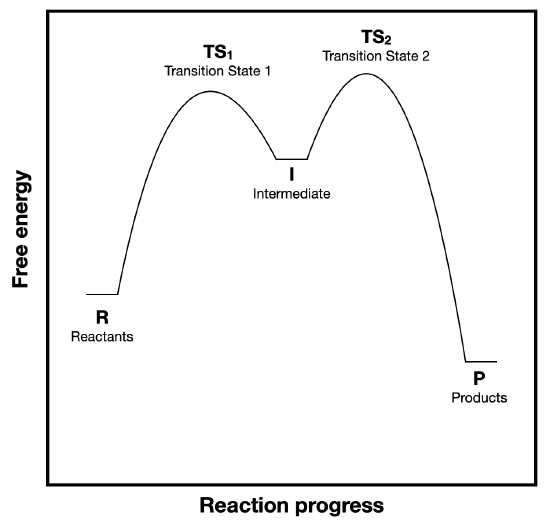
    Figure \(\PageIndex{1}\) is replicated below for convenience. This figure shows a reaction coordinate diagram for a two-step reaction.

    a. (\(\Delta G^{\circ}\)) and \(\Delta G^{\circ \ddagger}\)) are labeled on Figure \(\PageIndex{1}A\), but not on Figure \(\PageIndex{1}B\). Add the appropriate labels to diagram B. (copied below for convenience).

    b. Consider the energy barriers for the first and second steps and explain why the steady-state approximation is a valid assumption.
    Screen Shot 2022-07-13 at 4.47.42 PM.png

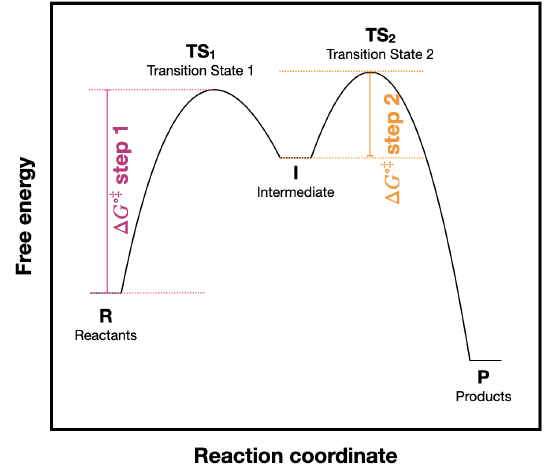
    Answer

    a) The activation energy for this reaction is the difference between R and \(TS_2\) because \(TS_2\) is the highest energy along the reaction pathway.
    clipboard_e2c28cb3160f6c528fd9b0dc9e3230c8b.png

    b) The activation energy for step 2 is much smaller than for step 1. This tells us that step 2 occurs faster than step 1. So, the concentration of intermediate should not increase over the course of the reaction, and it should react at least as fast as it is formed. The fact that the activation barrier for step 2 is less than for step one allows us to assume that [I] does not change over the course of the reaction. This should generally be true for all intermediates.

    clipboard_ea278c11803356d738a94b92761a6d831.png

    Exercise \(\PageIndex{1}\)

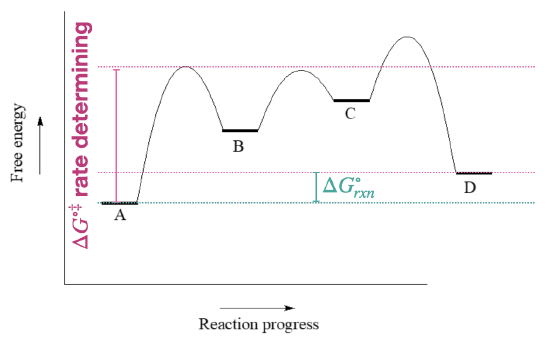
    Use the reaction coordinate diagram below to answer the questions.

    1. Is the overall reaction endergonic or exergonic in the forward (A to D) direction?
    2. How many steps does the reaction mechanism have?
    3. How many intermediates does the reaction mechanism have?
    4. Redraw the diagram if necessary. Add a label showing the energy barrier for the rate-determining step of the forward reaction.
    5. Add a label showing \(\ce{\Delta G^{\circ}_{rxn}}\) for the reverse reaction (D to A).
    6. What is the fastest reaction step, considering both the forward and reverse directions?

    The diagram has three transition states and two intermediates. The products have more energy than the reactants. Both intermediates have more energy than the reactans and products. The second intermediate has more energy than the first intermediate. The First transiton state and the third transiton state have almost equal activation energies. The second transition state has the lowest activation energy.

    Answer
    1. Is the overall reaction endergonic or exergonic in the forward (A to D) direction?
    2. How many steps does the reaction mechanism have?
    3. How many intermediates does the reaction mechanism have?
    4. The first step is rate determining since it has the largest activation barrier.
    5. \(\ce{\Delta G^{\circ}_{rxn}}\) for the reverse reaction (D to A) is the same as for the froward direction, with a revers of its sign.
      clipboard_e8d05f41baaed20de987ff8361e640f00.png
    6. The fastest step has the lowest barriers: this would be the step to/from B and C.

    Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

    Curated or created by Kathryn Haas

    This page titled 12.1: Introduction to Reactions of Metal Complexes is shared under a CC BY-NC 3.0 license and was authored, remixed, and/or curated by Kathryn Haas.