11.3.4: Symmetry labels for split terms
- Page ID
- 377932
While the free ion terms symbols are derived using Russell-Saunders terms, we only briefly discussed how the term symbols may be found from a character table upon ligand-field splitting. The symmetry labels (called Mulliken Labels) that are used in character tables to describe the symmetry of wavefunctions were described in a previous section (Section 4.3.3). Just as orbitals are wavefunctions that are described by the irreducible representations that are part of a character table, so are the terms. When we are discussing the terms of an octahedral complex, we can apply what we already know about octahedral symmetry and symmetry labels to understand how the terms labels are assigned.
Upon close inspection of any of the Tanabe-Sugano diagrams shown previously, or in the Resources Section, you may notice that each free ion term (listed at the right of the diagram) splits into a term or set of terms that retain the same multiplicity (the left superscript). Under an octahedral field, all terms have symbols \(A, B, E\) or \(T\) because they are singly, doubly, or triply degenerate. While some of these terms have subscripts "1" or "2", all the terms also have "\(g\)" subscripts due to the symmetry of the \(d\) orbitals. Some of the symbols might also look familiar, as they are similar to the labels you know for splitting of \(d\) orbitals, like \(E_g\) and \(T_{2g}\).
It is useful to know that under an octahedral field, the \(D, F, G, H, I\) terms split, but the terms \(S, P\) do not split. From inspection of the \(O_h\) character table, we find that free ion terms will split as follows:
\[\begin{array}{|l|l|} \hline \textbf{Free Ion Term} & \textbf{Terms under } O_h\\ \hline \text{S} & A_{1g} \\ P & T_{1g} \\ D & T_{2g}+E_g \\ F & A_{2g}+T_{2g}+T_{1g} \\ G & A_{1g}+E_g+T_{2g}+T_{1g} \\ H & E_g+T_{1g}+T_{1g}+T_{2g} \\ I & A_{1g}+A_{2g}+E_g+T_{1g}+T_{2g}+T_{2g} \\ \hline \end{array} \nonumber \]
The term symbols under an octahedral field have symmetry that matches symmetry of other elements within the molecule, including the \(d\)-orbitals. A reminder of their symmetry meanings is below (see also Section 4.3.3).
Each wavefunction (including terms) can be described by a Mulliken label (symmetry label). The labels used for terms in an octahedral ligand field are listed in the table below.
\(\begin{array}{l|l} \hline \textbf{Mulliken Labels} & \textbf{meaning}\\ \hline \text{A or B} & \text{singly degenerate} \\ E & \text{doubly degenerate} \\ T & \text{triply degenerate} \\ \hline \textbf{Subscripts} & \textbf{meaning} \\ \hline 1 & \text{symmetric to } \sigma_v \text{ or perpendicular } C_2 \\ 2 & \text{anti-symmetric to } \sigma_v \text{ or perpendicular } C_2 \\ g & \text{symmetric to inversion center} \\ u & \text{anti-symmetric to inversion center} \\ \hline \end{array} \)
We can use our knowledge of symmetry to derive the term labels for a given electron configuration under an octahedral field. Let's focus only on the capital letter that is assigned as the term symbol. Assignment of the octahedral term subscripts will not be described here, but are similar to assignment of these same subscripts to orbitals with matching symmetry.
For example, the \(d^1\) electron configuration has a free ion ground state term of \(^2D\). According to the table shown above, these terms will split into \(E_g\) and \(T_{2g}\) terms. Which would be its ground state term under an octahedral field? And which is the excited state term? To answer these questions we need to look at the electron configurations of the ground and excited states in an octahedral field. It is convenient to know that the term symbol under an octahedral field indicates the degeneracies of the related electron configurations.
Let's take a look at the electron configurations of the split \(d\)-orbitals to determine which term is the ground state. In the ground state of a \(d^1\) under an octahedral ligand field, there would be one electron in the \(t_{2g}\) orbitals, thus the electron configuration is \(t_{2g}^1e_g^0\). For simplicity we can consider only the cases where \(m_s\) values are \(+\frac{1}{2}\). There are three ways to put the electron in \(t_{2g}\) therefore, the ground state is triply degenerate, with a symbol "\(T\)". This is illustrated in the left panel of Figure \(\PageIndex{1}\).
In the excited state of a \(d^1\) under an octahedral ligand field, there would be one electron in the \(e_{g}\) orbitals, or a configuration of \(t_2g^0e_g^1\). There are two ways to arrange the electron with \(m_s=+\frac{1}{2}\) in the \(e_{g}\) orbitals (Figure \(\PageIndex{1}\), left). Therefore, the excited state is doubly degenerate, with a symbol "\(E\)".
In summary, the \(^2D\) free ion term for \(d^1\) splits into a lower-energy \(^2T_{2g}\) and a higher-energy \(^2E_g\) term under an octahedral field (Figure \(\PageIndex{1}\), left).
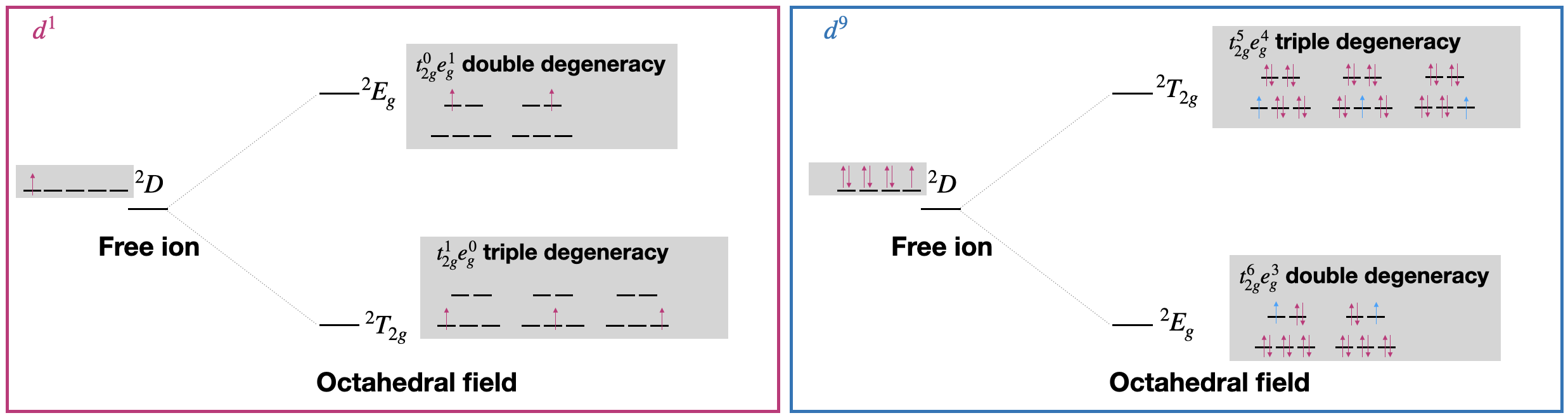
We could use a similar treatment to derive the relative energies and terms of a \(d^9\) ion in an octahedral field. The ground state term of \(d^9\) is the same as for \(d^1\): it is \(^2D\). If we look at the ground state and excited state electron configurations of a \(d^9\) ion, we find that the ground state configuration is \(t_{2g}^6 e_g^3\), which is doubly degenerate. On the other hand, the excited state has an electron configuration of \(t_{2g}^5 e_g^4\), and has triple degeneracy. In summary, in the case of \(d^9\), the \(^2D\) free ion term splits into a lower energy \(^2E_g\) term and a higher-energy \(^2T_{2g}\) term. This is exactly the opposite of \(d^1\)!
The \(d^1\) and \(d^9\) cases are opposite because they are related by what is said to be a "positive hole" concept. The \(d^9\) configuration could be derived from a \(d^{10}\) configuration with one positive "hole" (an electron removed). The positive hole is similar to the lone electron in \(d^1\) except that in the ground state, the hole is in \(e_g\), while the electron in \(d^1\) is in \(t_{2g}\); thus the two situations are exact opposites.
Just as \(d^1\) and \(d^9\) are related by the hole concept, so are \(d^4\) and \(d^6\). If you consider that \(d^1\) is the addition of one electron to the totally symmetric \(d^0\) case, then perhaps you can see how \(d^6\) is similar in that it is the addition of one electron to the totally symmetric \(d^5\) case. Thus, \(d^1\) and \(d^6\) have similar splittings under the octahedral field. Similarly, \(d^9\) is created by removing one electron from the totally symmetric case of \(d^{10}\) and \(d^4\) is created by removing one electron from \(d^5\). Thus \(d^4\) and \(d^9\) have identical splittings for their ground state free ion terms, which in these cases are a \(D\) term.
Due to the relationships between \(d^1, d^4, d^6,\) and \(d^9\), the same Orgel Diagram is used to show term splitting for these cases (Figure \(\PageIndex{2}\)). Orgel diagrams are yet another form of correlation diagrams.
Just as there are relationships between \(d^1,d^4,d^6,\) and \(d^9\), there are similar relationships between \(d^2,d^3,d^7,\) and \(d^8\), and there is an Orgel diagram that can represent the splitting of their relevant free-ion terms.
Tetrahedral splitting
Because tetrahedral field splitting has the opposite pattern to octahedral field splitting of the \(d\)-orbitals, there are relationships between tetrahedral and octahedral terms. In general, for a tetrahedral field with \(d^n\) electrons, the Tanabe-Sugano diagram of an octahedral diagram for \(d^{10-n}\) can be used to interpret the tetrahedral case. The Orgel diagrams are labeled in general terms for this reason. They can be applied to both tetrahedral and octahedral cases.
Jahn-Teller distortions
We can also see what would happen to the terms in the case of Jahn-Teller distortion. In the case of a Jahn-Teller distortion (most common for \(d^9\) and high-spin \(d^4\) where the \(e_g\) orbitals are asymmetrically occupied), we can use the degeneracy of orbital electron configurations to identify term labels. Let's walk through an example using the most simple case: a \(d^1\) metal ion (Figure \(\PageIndex{3}\)).
Jahn-teller usually causes a tetragonal distortion of an octahedron. This would be a change from \(O_h\) to \(D_{4h}\) symmetry.
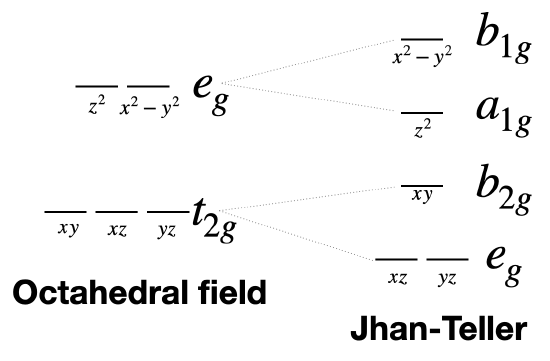
The \(t_{2g}\) orbitals (the set \(d_{xy}, d_{xz}, d_{yz}\) are split into \(e_g\) (\(d_{xz},d_{yz}\)) and \(b_{2g}\) (\(d_{xy}\)) by this symmetry change. Thus, we can expect any \(T_{2g}\) terms to be split similarly into \(E_g\) and \(B_{2g}\) terms by Jahn-Teller distortion. The \(e_g\) orbitals under \(O_h\) are split into \(a_1g\) (\(d^{z^2}\)) and \(b_1g\) (\(d_{x^2-y^2}\)) under \(D_{4h}\). Thus, we can expect \(E_g\) terms to be split into \(B_{1g}\) and \(A_{1g}\) terms by Jahn-Teller distortion (Figure \(\PageIndex{4}\)).
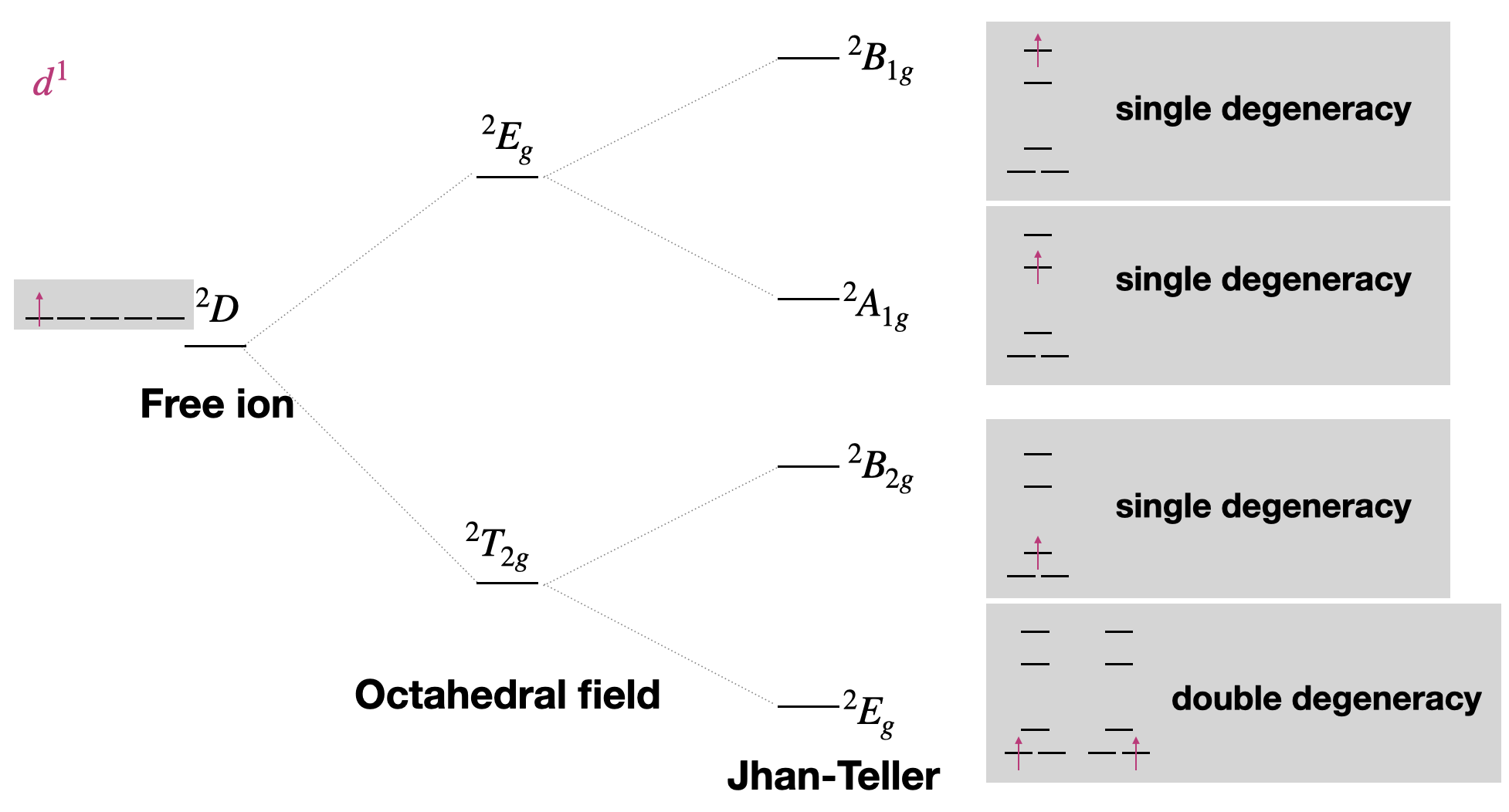
Just as \(d^1\) and \(d^9\) gave opposite order of their terms under an octahedral field, they also give opposite order of terms in the Jahn-Teller distortion.