8.7.1: The Group 14 Elements and the Many Allotropes of Carbon
- Page ID
- 199705
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As an element, carbon's ability to form strong multiple bonds enables it to form many allotropes, while the remaining elements in this group are network covalent or metallic solids.
Selected properties of the Group 14 elements are given in Table \(\sf{\PageIndex{1}}\).
| Property | Carbon | Silicon | Germanium | Tin | Lead |
|---|---|---|---|---|---|
| *The configuration shown does not include filled d and f subshells. | |||||
| †The values cited are for six-coordinate +4 ions in the most common oxidation state, except for C4+ and Si4+, for which values for the four-coordinate ion are estimated. | |||||
| ‡X is Cl, Br, or I. Reaction with F2 gives the tetrafluorides (EF4) for all group 14 elements, where E represents any group 14 element. | |||||
| atomic symbol | C | Si | Ge | Sn | Pb |
| atomic number | 6 | 14 | 32 | 50 | 82 |
| atomic mass (amu) | 12.01 | 28.09 | 72.64 | 118.71 | 207.2 |
| valence electron configuration* | 2s22p2 | 3s23p2 | 4s24p2 | 5s25p2 | 6s26p2 |
| melting point/boiling point (°C) | 4489 (at 10.3 MPa)/3825 | 1414/3265 | 938/2833 | 232/2586 | 327/1749 |
| density (g/cm3) at 25°C | 2.2 (graphite), 3.51 (diamond) | 2.33 | 5.32 | 7.27(white) | 11.30 |
| atomic radius (Å) | 1.70 | 2.10 | 2.11 | 2.17 | 2.02 |
| covalent radius (Å) | 0.75 | 1.14 | 1.20 | 1.40 | 1.45 |
| first ionization energy (kJ/mol) | 1086 | 787 | 762 | 709 | 716 |
| electron affinity (kJ/mol) | −122 | −134 | −119 | −107 | −35 |
| Pauling electronegativity | 2.55 | 1.90 | 2.01 | 1.96 | 1.8 |
| product of reaction with O2 | CO2, CO | SiO2 | GeO2 | SnO2 | PbO |
| type of oxide | acidic (CO2) | acidic neutral (CO) | amphoteric | amphoteric | amphoteric |
| product of reaction with N2 | none | Si3N4 | none | Sn3N4 | none |
| product of reaction with X2‡ | CX4 | SiX4 | GeX4 | SnX4 | PbX2 |
| product of reaction with H2 | CH4 | none | none | none | none |
As may be seen from the data in Table \(\sf{\PageIndex{1}}\), consistent with general atomic property trends, atomic radii increase down the group while electron affinities, ionization energies, and electronegativities generally decrease. The trends are not always monotonic, however, likely due to the impact of the d-block contraction on the atomic properties of Ge and also the lanthanide and actinide contractions on those of Sn and Pb.
From the common elemental forms of the group 14 elements in Table \(\sf{\PageIndex{1}}\) two trends are apparent:
- In keeping with the second row uniqueness principle, carbon forms a wider variety of allotropes than the other group 14 elements. Specifically, carbon's ability to form strong \(\pi\) bonds enables it to form delocalized sheet-like structures in the form of graphite and graphene (planar sheets) and nanotubes and fullerenes, which may be considered as sheets wrapped over to form tubes and ball-like structures, respectively.
- There is a decreasing tendency towards covalency down the group. While C, Si, and Ge form network covalent structures and Pb a metallic one, tin forms both network covalent and metallic structures, which differ so slightly in their stability that the metallic form interconverts to the network covalent one above 13\(^{\circ}\)C.
Carbon's ability to form strong multiple bonds enables it to form a host of molecular and network covalent allotropes
Carbon's ability to form strong multiple bonds enables it to form a host of molecular and network covalent allotropes. Some of these allotropes have been known since ancient times; some are a focus of much active research. The major classes of allotropes include:
1. \(\alpha\)- and \(\beta\)-Graphite. The \(\alpha\) form of graphite is the most stable carbon allotrope. It is formed naturally through the decomposition of carbonaceous material in sediments but may also be made synthetically by vaporizing the Si out of SiC.
\[\sf{SiC~~\overset{\Delta}{\longrightarrow}~~~C(s)~~+~~Si(g)} \nonumber \]
The structure of \(\alpha\)-graphite consists of hexagonal layers of interconnected rings of graphene sheets, the structure of which is shown in Scheme \(\sf{\PageIndex{I}}\).
Scheme \(\sf{\PageIndex{I}}\). One resonance structure depiction of part of a graphene sheet.
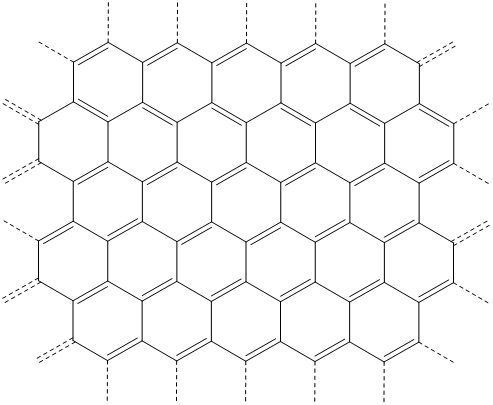
All the carbons in the graphene sheet are trigonal planar and connected by a network of covalent bonds that may be adequately described as involving sigma overlaps between sp2 -orbitals and a delocalized \(\pi\) bond network. This delocalized \(\pi\) bonding system involves a half-filled valence band of \(\pi\) type orbitals and is responsible for graphite's good electrical conductivity.
In terms of the impact of the delocalized \(pi\) bonds on graphite's structure, it ensures that the graphene sheets are planar with delocalized \(\pi\) clouds above and below the carbon plane. Because of this, the sheets may be stacked together in various arrangements in which the carbons in adjacent layers may be eclipsed or staggered with respect to one another, as shown in Figure \(\sf{\PageIndex{1}}\). The stable \(\alpha\)-graphite form possesses staggered layers alternating an AB pattern, while in the slightly less stable \(\beta\)-graphite, the layers are staggered in an ABC arrangement (Figure \(\sf{\PageIndex{1b}}\)).
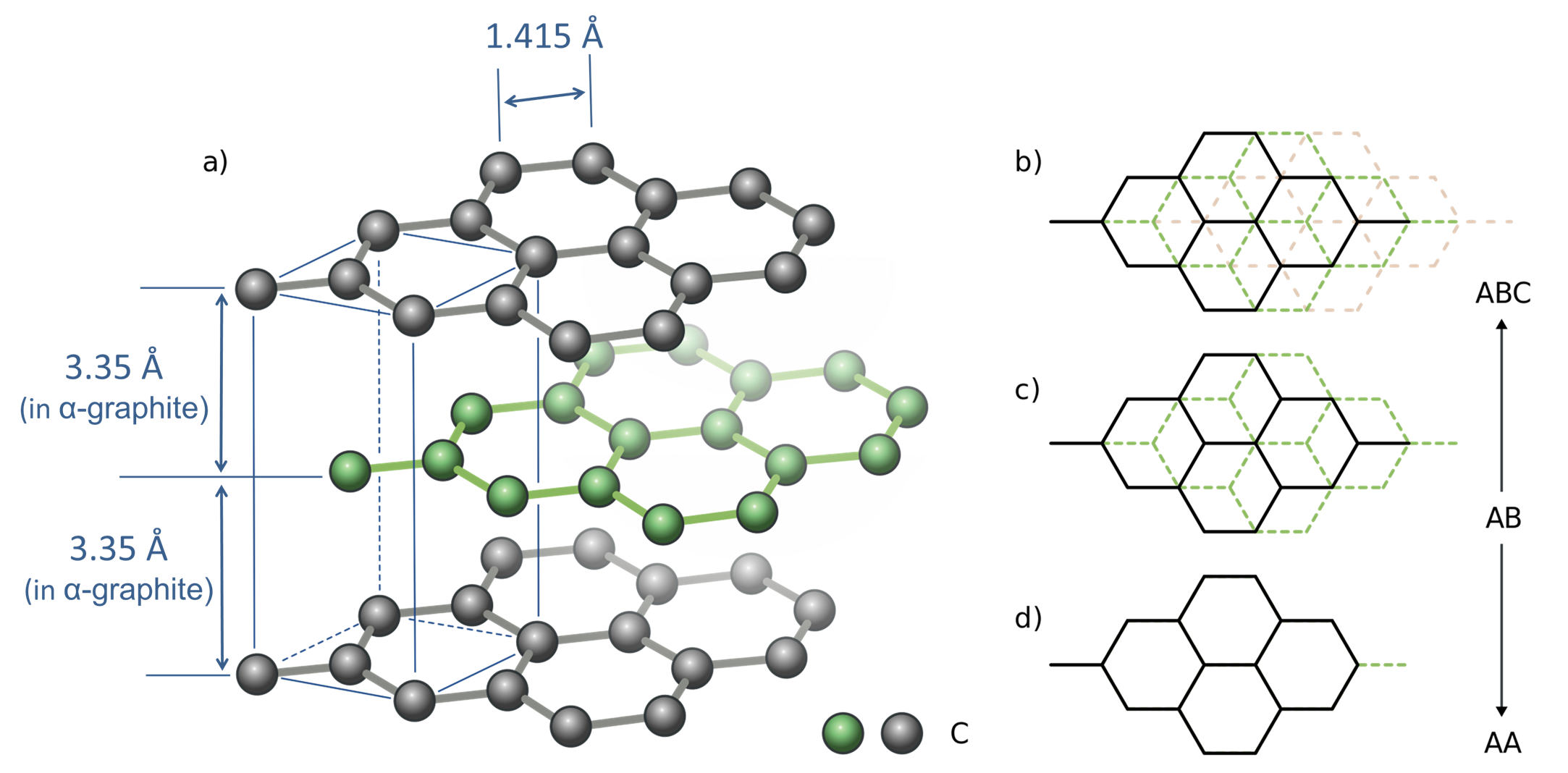
Since the forces between the graphene layers do not vary much as the sheets move past one another, it is relatively easy for layer slip to occur; graphite thus functions effectively as a lubricant. In addition, it is possible to exfoliate individual graphene sheets using scotch tape and chemical exfoliation methods.
2. Graphene. Individual graphene sheets like that depicted in Scheme \(\sf{\PageIndex{I}}\) have been the subject of intense experimental and theoretical investigation as a 2D nanomaterial. Owing to the strong carbon-carbon bonds that hold the sheet together, defect-free graphene is the strongest material known, albeit a brittle one; it also has a band structure that makes it a good conductor of electricity and leads to unusual optical properties. Among the latter, even a single graphene layer is visible to the naked eye, as shown in Figure \(\sf{\PageIndex{2}}\).

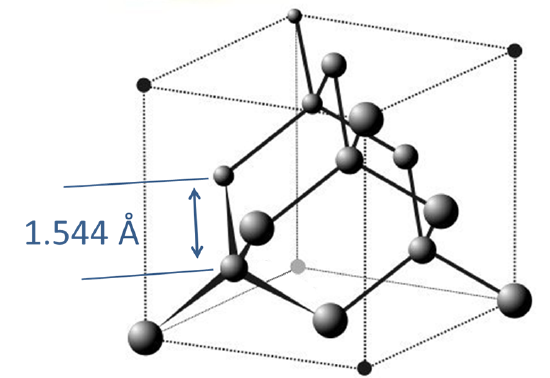
3. Diamond and Lonsdaleite. When subjected to extremes of heat and pressure, graphite converts to its more dense diamond allotrope, in which all the carbons are tetrahedral and held together by sigma bonds, as shown in Figure \(\sf{\PageIndex{3}}\). In this structure, all the carbons are tetrahedral and connected in chair conformation rings. As might be expected from such a tightly interconnected structure, diamond is extremely hard, although analogous structures which also possess chair form rings, specifically Wurtzite-like hexagonal BN and its all-carbon analogue Lonsdaleite, are even harder. As might be expected from diamond's all-\(\sigma\) structure, it is a poor electrical conductor, and the 1.544 Å C-C bond length in diamond is longer than the 1.415 Å C-C bond length in graphite (1.415 Å).
4. Fullerenes. Since the late 1980s discovery of the sixty-carbon European football (soccer ball) shaped buckminsterfullerene shown in Figure \(\sf{\PageIndex{4A}}\), it has been recognized that such molecules have long been present in soot, carbon black, and related materials. Produced today by electrolytic or laser ablation or pyrolysis, a large number of such structures have been produced, some of which are shown in Figure \(\sf{\PageIndex{4B}}\).
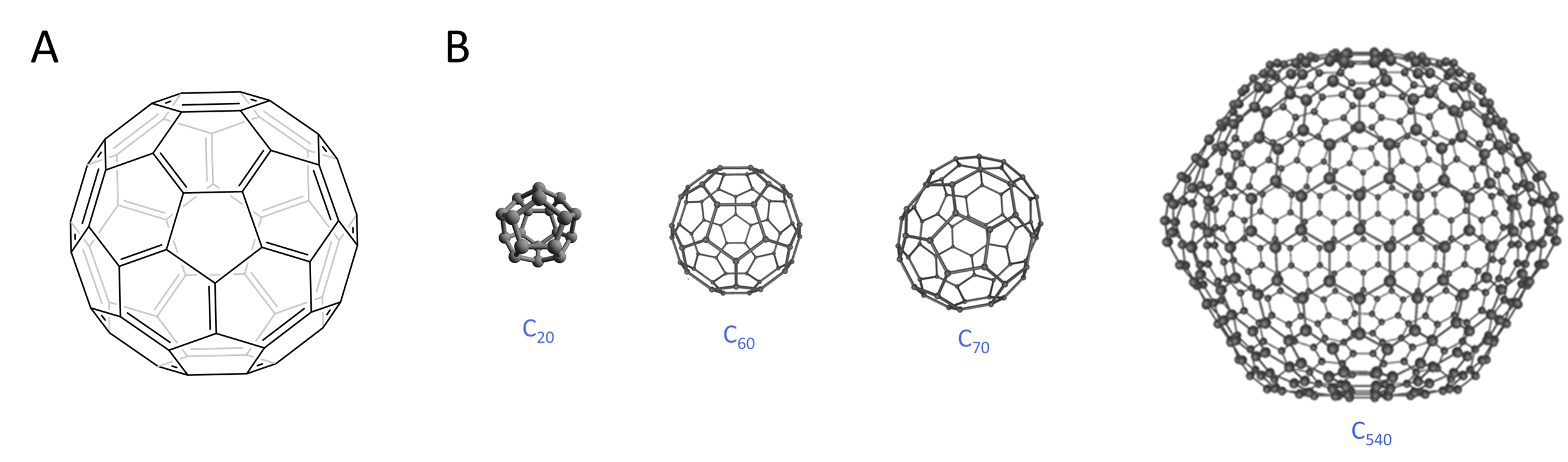 Figure \(\sf{\PageIndex{4}}\). Structures of several fullerenes: (A) buckminsterfullerene, C60, named after the American architect Buckminster Fuller, who popularized the use of geodesic domes; (B) C70, and (C) C540 The image of C20 is taken from By Perditax - Own work, CC0, commons.wikimedia.org/w/inde...curid=15480223; the 3D images of C60, C70, and C540 are remixed from the image Created by Michael Ströck (mstroeck) - Created by Michael Ströck (mstroeck), CC BY-SA 3.0, commons.wikimedia.org/w/inde...p?curid=584786
Figure \(\sf{\PageIndex{4}}\). Structures of several fullerenes: (A) buckminsterfullerene, C60, named after the American architect Buckminster Fuller, who popularized the use of geodesic domes; (B) C70, and (C) C540 The image of C20 is taken from By Perditax - Own work, CC0, commons.wikimedia.org/w/inde...curid=15480223; the 3D images of C60, C70, and C540 are remixed from the image Created by Michael Ströck (mstroeck) - Created by Michael Ströck (mstroeck), CC BY-SA 3.0, commons.wikimedia.org/w/inde...p?curid=584786
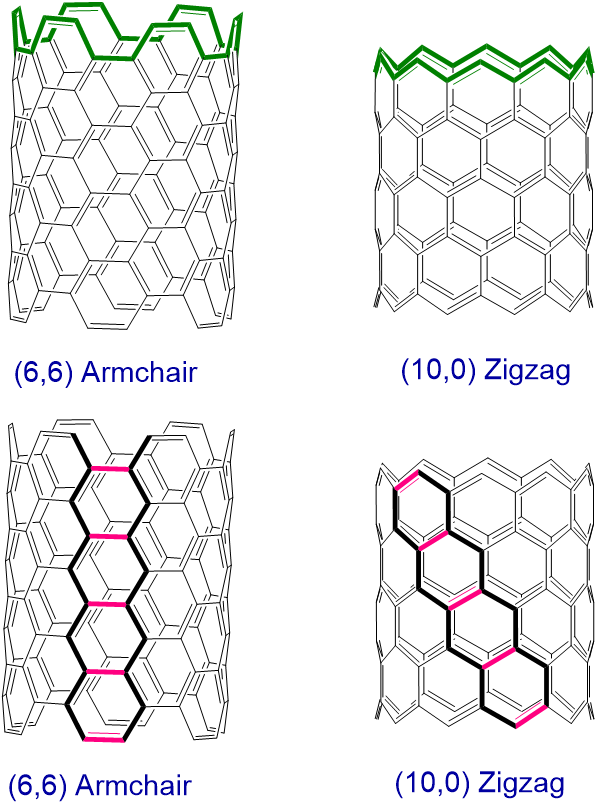
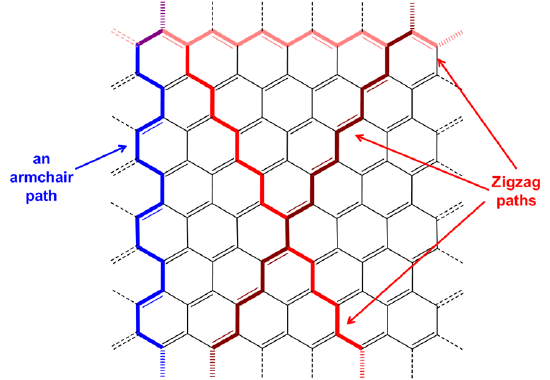
As shown in Figure \(\sf{\PageIndex{6}}\), the overall linear chains of connected carbon atoms within a graphene sheet can be classified as taking on either a zigzag or armchair arrangement. Nanotubes then are classified as armchair or zigzag based on the arrangement of the bonds perpendicular to the tube axis (Figure \(\sf{\PageIndex{7}}\), top). Alternatively, armchair nanotubes may be envisioned as formed by connecting the zigzag path ends of a graphene sheet in which the direction of the zigzag path is oriented along the nanotube axis, while in zigzag nanotubes the connected zigzag paths are angled relative to the helix axis (Figure \(\sf{\PageIndex{7}}\), bottom).
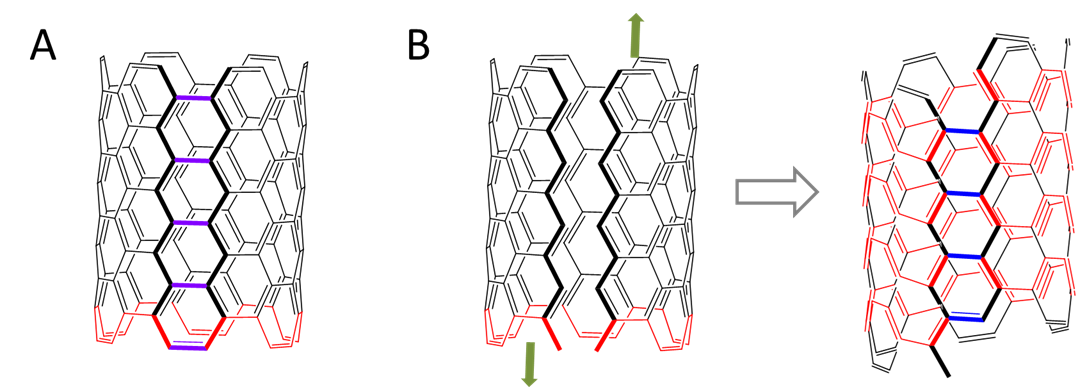
In ordinary carbon nanotubes the armchair or zigzag path around the tube forms a closed loop. Such carbon nanotubes are relatively linear. In helical nanotubes like that shown in Figure \(\sf{\PageIndex{7}}\), the armchair or zigzag paths form a helical spiral around the nanotube surface instead. In order for this to take place, the carbon rings cannot be perfectly hexagonal but are instead twisted, and to relieve the resulting strain helical nanotubes take on a coiled shape.
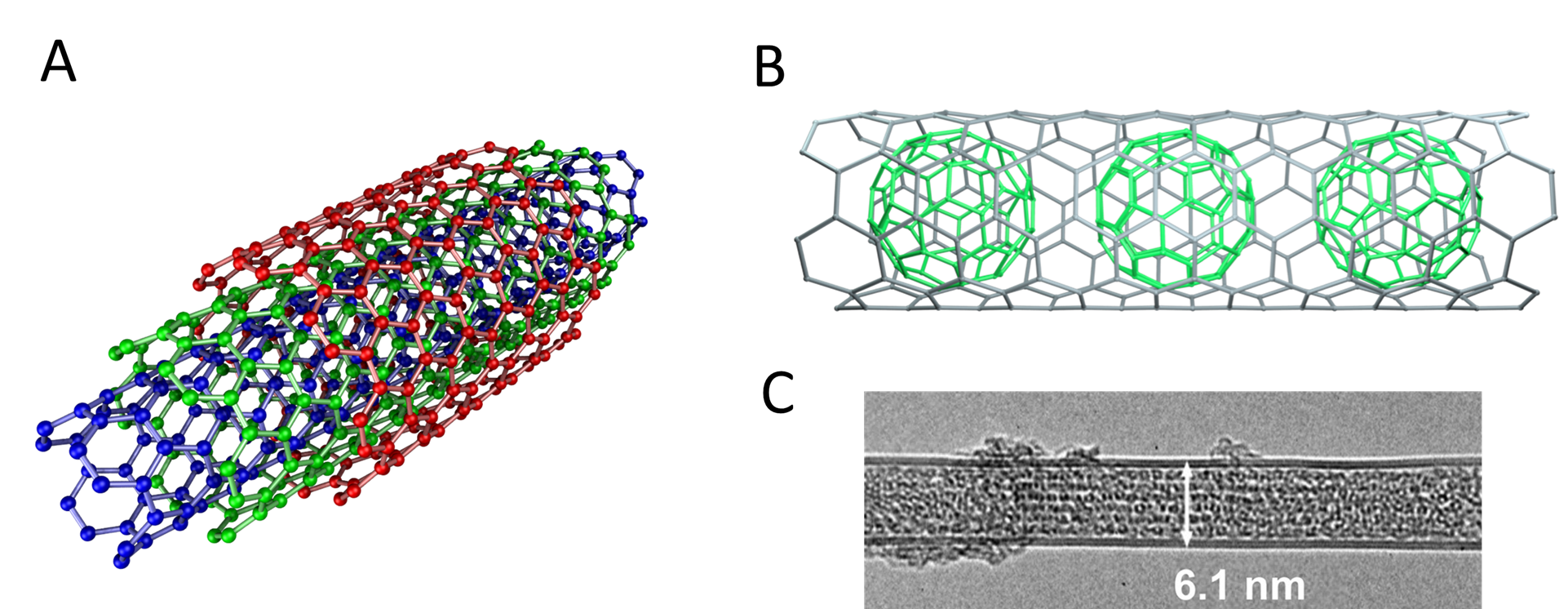
Depending on the size of the nanotube, it is sometimes even possible to nest multiple nanotubes inside one another, to "bud" fullerenes off the side of a nanotube, or even to fit fullerenes inside to give a "carbon peapod". Some of the possibilities are depicted in Figure \(\sf{\PageIndex{8}}\).
The chemical properties of fullerenes and nanotubes reflect their structure in the following ways:
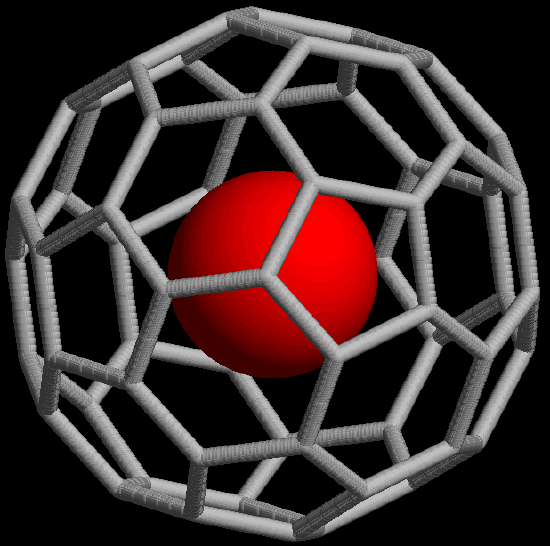
- They possess a delocalized \(\pi\) structure and so can undergo facile oxidation and reduction reactions. For instance, buckminsterfullerene can be electrochemically reduced in six successive one-electron steps to give C606-. Similar reductions can occur by reacting a fullerene with an active metal. In many cases this simply results in a salt of a fulleride anion, but in some cases the metal goes inside the fullerene cage to give an endohedral fullerene, designated M@C60. A model of such a fullerene is given in Figure \(\sf{\PageIndex{9}}\).
- The carbons in these systems are all quaternary and so generally only undergo addition reactions, not substitutions.
- While the planar sheets of graphite contain trigonal planar carbons, the carbons in fullerenes and nanotubes must be slightly bent into a pyramidal shape in order to accommodate the concavity of those structures. This results in considerable steric strain that can be relieved when addition occurs at a carbon to render it tetrahedral. Because of this, fullerenes undergo a variety of nucleophilic and cycloaddition reactions, primarily at the C=C bonds joining two six-membered rings.
Readers desiring a more thorough presentation of the chemistry of fullerenes are invited to read this summary of carbon nanomaterials by Andrew Barron of Rice University.
6. Vitreous carbon. Glass-like carbon, commonly referred to as glassy or vitreous carbon, is believed to consist of a mixture of concave graphene-like sheets, similar to those in nanotubes and fullerenes but not completely wrapped to form closed balls or tubes. Such forms of carbon are commonly used in electrode materials in electrochemistry (e.g., glassy carbon electrodes).
7. High-carbon content amorphous materials. These are technically not a single form or a pure allotrope but rather a family of high-carbon content materials that include amorphous carbon, carbon black, soot, pyrolyzed coal, coal, and charcoal. These contain varying amounts of hydrocarbons (particularly polycyclic aromatic hydrocarbons) and other organic material. Many of these materials contain small crystallites of diamond and graphite-like regions interconnected by an amorphous matrix of carbon-rich material. Some representative structures are given in Figure \(\sf{\PageIndex{10}}\).
8. Graphyne - a possible future carbon allotrope? The discovery of fullerene and carbon nanotube structures held together exclusively by interconnected C-C and C=C bonds raises the issue of whether it might be possible to construct forms of carbon that include or are even primarily comprised of C≡C bonds. These materials, called graphynes, by analogy with the double bonded structure of graphene, are predicted to be theoretically stable but as yet have been neither observed in nature nor made experimentally. A selection of proposed graphyne structures is given in Figure \(\sf{\PageIndex{11}}\).

A number of group 14 isotopes find use in analytical applications. These include:
13C, a spin 1/2 NMR active isotope comprising 1% of natural carbon. It is widely used in carbon-13 NMR to structurally characterize organic and organometallic compounds. For more information on carbon 13 NMR and its use in organic chemistry see this page.
14C, an unstable isotope that occurs at ~ 1 parts per trillion in the atmosphere and undergoes radioactive decay with a half-life of 5730 years. Since the level of 14C in organisms is approximately equal to atmospheric levels at their time of death and decays thereafter, the ratio of 14C to 12C in a biologically-derived sample may be used to estimate the age of objects ~60,000 years old or less. For more information on radiocarbon dating see this chem libre texts page.
29Si, a spin 1/2 NMR active isotope comprising ~5% of naturally occurring silicon. Silicon-29 NMR is useful as a structural tool for characterizing silicon compounds ranging from glasses to organosilanes. Although there is not yet a Chem Libre texts page describing the technique, a brief introduction may be found here.
73Ge, a spin 9/2 nucleus, and spin 1/2 115Sn, 117Sn, 119Sn, and 207Pb are also NMR active isotopes that can be used to structurally characterize compounds of these elements. Their use is beyond the scope of this introductory text but for those interested, more information about the use of these nuclei in NMR is available for Ge, Sn, and Pb. In addition 73Ge is Mössbauer active, although relatively few examples of its use in the characterization of Ge in Ge-containing materials exist.
References
1. Atomic and physical property data are taken from those listed by the Royal Society of Chemistry at https://www.rsc.org/periodic-table. Many are rounded to a smaller number of significant figures. The structure images are taken from
2. Lee, C.; Wei, X.; Kysar, J. W.; Hone, J., Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321 (5887), 385-388.
3. Barzegar, H. R.; Gracia-Espino, E.; Yan, A.; Ojeda-Aristizabal, C.; Dunn, G.; Wågberg, T.; Zettl, A., C60/Collapsed Carbon Nanotube Hybrids: A Variant of Peapods. Nano Letters 2015, 15 (2), 829-834.
Contributors and Attributions
Stephen Contakes, Westmont College

