Semiconductors, as we noted above, are somewhat arbitrarily defined as insulators with band gap energy < 3.0 eV (~290 kJ/mol). This cutoff is chosen because, as we will see, the conductivity of undoped semiconductors drops off exponentially with the band gap energy and at 3.0 eV it is very low. Also, materials with wider band gaps (e.g. SrTiO3, Egap = 3.2 eV) do not absorb light in the visible part of the spectrum
There are a number of places where we find semiconductors in the periodic table:
- Early transition metal oxides and nitrides, especially those with d0 electron counts such as TiO2, TaON, and WO3
- Oxides of later 3d elements such as Fe2O3, NiO, and Cu2O
- Layered transition metal chalcogenides with d0, d2 and d6 electron counts including TiS2, ZrS2, MoS2, WSe2, and PtS2
- d10 copper and sliver halides, e.g., CuI, AgBr, and AgI
- Zincblende- and wurtzite-structure compounds of the p-block elements, especially those that are isoelectronic with Si or Ge, such as GaAs and CdTe. While these are most common, there are other p-block semiconductors that are not isoelectronic and have different structures, including GaS, PbS, and Se.
|

A 2" wafer cut from a GaAs single crystal. GaAs, like many p-block semiconductors, has the zincblende structure.
|
The p-block octet semiconductors are by far the most studied and important for technological applications, and are the ones that we will discuss in detail.
Zincblende- and wurtzite-structure semiconductors have 8 valence electrons per 2 atoms. These combinations include 4-4 (Si, Ge, SiC,…), 3-5 (GaAs, AlSb, InP,…), 2-6 (CdSe, HgTe, ZnO,…), and 1-7 (AgCl, CuBr,…) semiconductors. Other variations that add up to an octet configuration are also possible, such as CuIInIIISe2, which has the chalcopyrite structure, shown at the right.
|
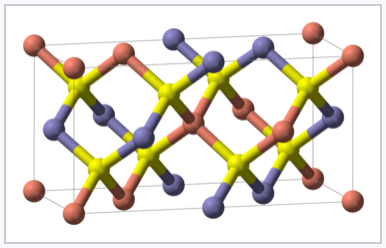
The chalcopyrite structure is adopted by ABX2 octet semiconductors such as CuIInIIISe2 and CdIISnIVP2. The unit cell is doubled relative to the parent zincblende structure because of the ordered arrangement of cations. Each anion (yellow) is coordinated by two cations of each type (blue and red).
|
How does the band gap energy vary with composition? There are two important trends
(1) Going down a group in the periodic table, the gap decreases:
-
-
- C (diamond) > Si > Ge > α-Sn
Egap (eV): 5.4 1.1 0.7 0.0
This trend can be understood by recalling that Egap is related to the energy splitting between bonding and antibonding orbitals. This difference decreases (and bonds become weaker) as the principal quantum number increases.
(2) For isoelectronic compounds, increasing ionicity results in a larger band gap.
-
-
- Ge < GaAs < ZnSe
- 0.7 1.4 2.8 eV
-
-
- Sn < InSb < CdTe < AgI
- 0.0 0.2 1.6 2.8 eV
This trend can also be understood from a simple MO picture, as we discussed in Ch. 2. As the electronegativity difference Δχ increases, so does the energy difference between bonding and antibonding orbitals.
The band gap is a very important property of a semiconductor because it determines its color and conductivity. Many of the applications of semiconductors are related to band gaps:
- Narrow gap materials (HgxCd1-xTe, VO2, InSb, Bi2Te3) are used as infrared photodetectors and thermoelectrics (which convert heat to electricity).
- Wider gap materials (Si, GaAs, GaP, GaN, CdTe, CuInxGa1-xSe2) are used in electronics, light-emitting diodes, and solar cells.
|
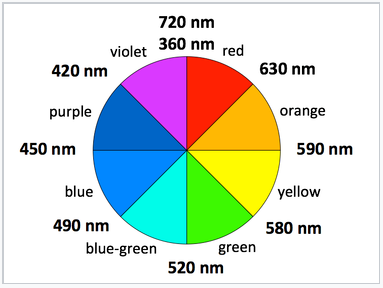
Color wheel showing the colors and wavelengths of emitted light.
|
Semiconductor solid solutions such as GaAs1-xPx have band gaps that are intermediate between the end member compounds, in this case GaAs and GaP (both zincblende structure). Often, there is a linear relation between composition and band gap, which is referred to as Vegard's Law. This "law" is often violated in real materials, but nevertheless offers useful guidance for designing materials with specific band gaps. For example, red and orange light-emitting diodes (LED's) are made from solid solutions with compositions of GaP0.40As0.60 and GaP0.65As0.35, respectively. Increasing the mole fraction of the lighter element (P) results in a larger band gap, and thus a higher energy of emitted photons.
Colors of semiconductors
The color of absorbed and emitted light both depend on the band gap of the semiconductor. Visible light covers the range of approximately 390-700 nm, or 1.8-3.1 eV. The color of emitted light from an LED or semiconductor laser corresponds to the band gap energy and can be read off the color wheel shown at the right.
|

Fe2O3 powder is reddish orange because of its 2.2 eV band gap
|
The color of absorbed light includes the band gap energy, but also all colors of higher energy (shorter wavelength), because electrons can be excited from the valence band to a range of energies in the conduction band. Thus semiconductors with band gaps in the infrared (e.g., Si, 1.1 eV and GaAs, 1.4 eV) appear black because they absorb all colors of visible light. Wide band gap semiconductors such as TiO2 (3.0 eV) are white because they absorb only in the UV. Fe2O3 has a band gap of 2.2 eV and thus absorbs light with λ < 560 nm. It thus appears reddish-orange (the colors of light reflected from Fe2O3) because it absorbs green, blue, and violet light. Similarly, CdS (Egap = 2.6 eV) is yellow because it absorbs blue and violet light.
Electrons and holes in semiconductors
Pure (undoped) semiconductors can conduct electricity when electrons are promoted, either by heat or light, from the valence band to the conduction band. The promotion of an electron (e-) leaves behind a hole (h+) in the valence band. The hole, which is the absence of an electron in a bonding orbital, is also a mobile charge carrier, but with a positive charge. The motion of holes in the lattice can be pictured as analogous to the movement of an empty seat in a crowded theater. An empty seat in the middle of a row can move to the end of the row (to accommodate a person arriving late to the movie) if everyone moves over by one seat. Because the movement of the hole is in the opposite direction of electron movement, it acts as a positive charge carrier in an electric field.
The opposite process of excitation, which creates an electron-hole pair, is their recombination. When a conduction band electron drops down to recombine with a valence band hole, both are annihilated and energy is released. This release of energy is responsible for the emission of light in LEDs.
|
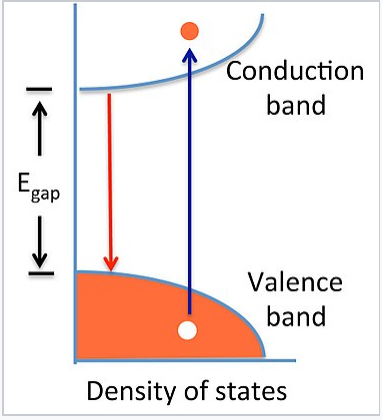
An electron-hole pair is created by adding heat or light energy E > Egap to a semiconductor (blue arrow). The electron-hole pair recombines to release energy equal to Egap (red arrow).
|
At equilibrium, the creation and annihilation of electron-hole pairs proceed at equal rates. This dynamic equilibrium is analogous to the dissociation-association equilibrium of H+ and OH- ions in water. We can write a mass action expression:
\(n \times p = K_{eq} = n_{i}^{2}\)
where n and p represent the number density of electrons and holes, respectively, in units of cm-3. The intrinsic carrier concentration, ni, is equal to the number density of electrons or holes in an undoped semiconductor, where n = p = ni.
Note the similarity to the equation for water autodissociation:
\([H^{+}][OH^{-}] = K_{w}\)
By analogy, we will see that when we increase n (e.g., by doping), p will decrease, and vice-versa, but their product will remain constant at a given temperature.
Temperature dependence of the carrier concentration. Using the equations \(K_{eq} = e^{(\frac{- \Delta G^{o}}{RT})} \) and \(\Delta G^{o} = \Delta H^{o} - T \Delta S^{o}\), we can write:
\[ n \times p = n_{i}^{2} = e^{(\frac{\Delta S^{o}} {R})} e^{(\frac{- \Delta H^{o}}{RT})}\]
The entropy change for creating electron hole pairs is given by:
\[\Delta S^{o} = R ln (N_{V}) + R ln (N_{V}) = R ln (N_{C}N_{V})\]
where NV and NC are the effective density of states in the valence and conduction bands, respectively.
and thus we obtain
\[n_{i}^{2} = N_{C}N_{V} e^{({- \Delta H^{o}}{RT})}\]
Since the volume change is negligible, \(\Delta H^{o} \approx \Delta E^{o}\), and therefore \(\frac {\Delta H^{o}}{R} \approx \frac{E_{gap}}{k}\), from which we obtain
\[n_{i}^{2} = N_{C}N_{V} e^{(\frac{-E_{gap}}{kT})}\]
and finally
\[\mathbf{n= p = n_{i} = (N_{C}N_{V})^{\frac{1}{2}} e^{(\frac{-E_{gap}}{2kT})}}\]
For pure Si (Egap = 1.1 eV) with N ≈ 1022/cm3, we can calculate from this equation a carrier density ni of approximately 1010/cm3 at 300 K. This is about 12 orders of magnitude lower than the valence electron density of Al, the element just to the left of Si in the periodic table. Thus we expect the conductivity of pure semiconductors to be many orders of magnitude lower than those of metals.
Conductivity of intrinsic semiconductors
The conductivity (σ) is the product of the number density of carriers (n or p), their charge (e), and their mobility (µ). Recall from Chapter 6 that µ is the ratio of the carrier drift velocity to the electric field and has units of cm2/Volt-second. Typically electrons and holes have somewhat different mobilities (µe and µh, respectively) so the conductivity is given by:
\[\sigma = ne\mu_{e} + pe\mu_{h}\]
For either type of charge carrier, we recall from Ch. 6 that the mobility μ is given by:
\[\mu = \frac{v_{drift}}{E} = \frac{e\tau}{m}\]
where e is the fundamental unit of charge, τ is the scattering time, and m is the effective mass of the charge carrier.
Taking an average of the electron and hole mobilities, and using n = p, we obtain
\[\mathbf{\sigma= \sigma_{o} e^{(\frac{-E_{gap}}{2kT})}}, \: where \: \sigma_{o} = 2(N_{C}N_{V})^{\frac{1}{2}}e\mu\]
By measuring the conductivity as a function of temperature, it is possible to obtain the activation energy for conduction, which is Egap/2. This kind of plot, which resembles an Arrhenius plot, is shown at the right for three different undoped semiconductors. The slope of the line in each case is -Egap/2k.
|
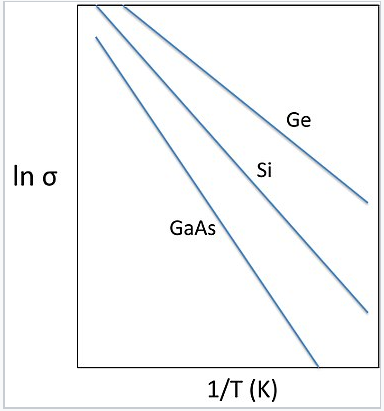
Plots of ln(σ) vs. inverse temperature for intrinsic semiconductors Ge (Egap = 0.7 eV), Si (1.1 eV) and GaAs (1.4 eV). The slope of the line is -Egap/2k.
|
Doping of semiconductors. Almost all applications of semiconductors involve controlled doping, which is the substitution of impurity atoms, into the lattice. Very small amounts of dopants (in the parts-per-million range) dramatically affect the conductivity of semiconductors. For this reason, very pure semiconductor materials that are carefully doped - both in terms of the concentration and spatial distribution of impurity atoms - are needed.
n- and p-type doping. In crystalline Si, each atom has four valence electrons and makes four bonds to its neighbors. This is exactly the right number of electrons to completely fill the valence band of the semiconductor. Introducing a phosphorus atom into the lattice (the positively charged atom in the figure at the right) adds an extra electron, because P has five valence electrons and only needs four to make bonds to its neighbors. The extra electron, at low temperature, is bound to the phosphorus atom in a hydrogen-like molecular orbital that is much larger than the 3s orbital of an isolated P atom because of the high dielectric constant of the semiconductor. In silicon, this "expanded" Bohr radius is about 42 Å, i.e., 80 times larger than in the hydrogen atom. The energy needed to ionize this electron – to allow it to move freely in the lattice - is only about 40–50 meV, which is not much larger the thermal energy (26 meV) at room temperature. Therefore the Fermi level lies just below the conduction band edge, and a large fraction of these extra electrons are promoted to the conduction band at room temperature, leaving behind fixed positive charges on the P atom sites. The crystal is n-doped, meaning that the majority carrier (electron) is negatively charged.
Alternatively, boron can be substituted for silicon in the lattice, resulting in p-type doping, in which the majority carrier (hole) is positively charged. Boron has only three valence electrons, and "borrows" one from the Si lattice, creating a positively charged hole that exists in a large hydrogen-like orbital around the B atom. This hole can become delocalized by promoting an electron from the valence band to fill the localized hole state. Again, this process requires only 40–50 meV, and so at room temperature a large fraction of the holes introduced by boron doping exist in delocalized valence band states. The Fermi level (the electron energy level that has a 50% probability of occupancy at zero temperature) lies just above the valence band edge in a p-type semiconductor.
|
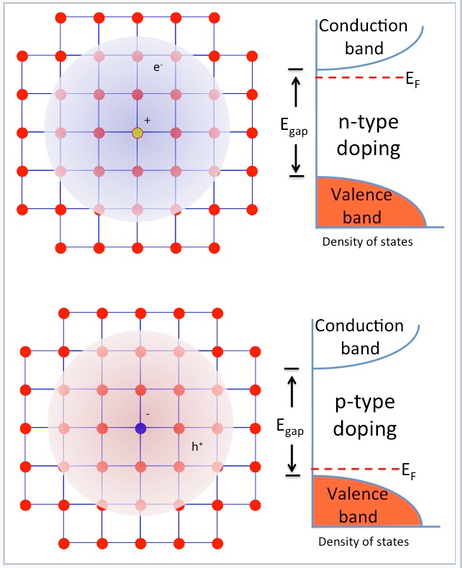
n- and p-type doping of semiconductors involves substitution of electron donor atoms (light orange) or acceptor atoms (blue) into the lattice. These substitutions introduce extra electrons or holes, respectively, which are easily ionized by thermal energy to become free carriers. The Fermi level of a doped semiconductor is a few tens of mV below the conduction band (n-type) or above the valence band (p-type).
|
As noted above, the doping of semiconductors dramatically changes their conductivity. For example, the intrinsic carrier concentration in Si at 300 K is about 1010 cm-3. The mass action equilibrium for electrons and holes also applies to doped semiconductors, so we can write:
\[n \times p = n_{i}^{2} = 10^{20} cm^{-6} \: at \: 300K\]
If we substitute P for Si at the level of one part-per-million, the concentration of electrons is about 1016 cm-3, since there are approximately 1022 Si atoms/cm3 in the crystal. According to the mass action equation, if n = 1016, then p = 104 cm-3. There are three consequences of this calculation:
- The density of carriers in the doped semiconductor (1016 cm-3) is much higher than in the undoped material (~1010 cm-3), so the conductivity is also many orders of magnitude higher.
- The activation energy for conduction is only 40–50 meV, so the conductivity does not change much with temperature (unlike in the intrinsic semiconductor)
- The minority carriers (in this case holes) do not contribute to the conductivity, because their concentration is so much lower than that of the majority carrier (electrons).
Similarly, for p-type materials, the conductivity is dominated by holes, and is also much higher than that of the intrinsic semiconductor.
Chemistry of semiconductor doping. Sometimes it is not immediately obvious what kind of doping (n- or p-type) is induced by "messing up" a semiconductor crystal lattice. In addition to substitution of impurity atoms on normal lattice sites (the examples given above for Si), it is also possible to dope with vacancies - missing atoms - and with interstitials - extra atoms on sites that are not ordinarily occupied. Some simple rules are as follows:
- For substitutions, adding an atom to the right in the periodic table results in n-type doping, and an atom to the left in p-type doping.
For example, when TiO2 is doped with Nb on some of the Ti sites, or with F on O sites, the result is n-type doping. In both cases, the impurity atom has one more valence electron than the atom for which it was substituted. Similarly, substituting a small amount of Zn for Ga in GaAs, or a small amount of Li for Ni in NiO, results in p-type doping.
- Anion vacancies result in n-type doping, and cation vacancies in p-type doping.
Examples are anion vacancies in CdS1-x and WO3-x, both of which give n-type semiconductors, and copper vacancies in Cu1-xO, which gives a p-type semiconductor.
- Interstitial cations (e.g. Li) donate electrons to the lattice resulting in n-type doping. Interstitial anions are rather rare but would result in p-type doping.
Sometimes, there can be both p- and n-type dopants in the same crystal, for example B and P impurities in a Si lattice, or cation and anion vacancies in a metal oxide lattice. In this case, the two kinds of doping compensate each other, and the doping type is determined by the one that is in higher concentration. A dopant can also be present on more than one site. For example, Si can occupy both the Ga and As sites in GaAs, and the two substitutions compensate each other. Si has a slight preference for the Ga site, however, resulting in n-type doping.








