6.3.4: Brønsted-Lowry Superacids and the Hammett Acidity Function
- Page ID
- 154234
Acids with an acidity greater than that of sulfuric acid are termed superacids.
Superacids are able to dissociate completely because when they do so they give an extremely stable anion in which the residual negative charge is distributed among multiple electronegative atoms. For example, in mixtures of \(\ce{HF}\) and antimony pentaflouride the dissociation of a hydrogen ion from the \(\ce{HF}\) is promoted by the formation of a Lewis acid-base adduct between the \(\ce{HF}\) flouride and \(\ce{SbF_5}\).

This gives extremely stable anions like \(\ce{SbF_6^{-}}\) and \(\ce{Sb_2F_{11}^{-}}\), in which a single negative charge is delocalized among many electronegative groups and atoms; of these, \(CF_3\) and F are particularly common.

Superacids are able to protonate species that would otherwise act as neutral or even acidic species in water or aprotic media. Phosphoric, nitric, carboxylic, and other ordinary acids are all protonated when dissolved in superacids:
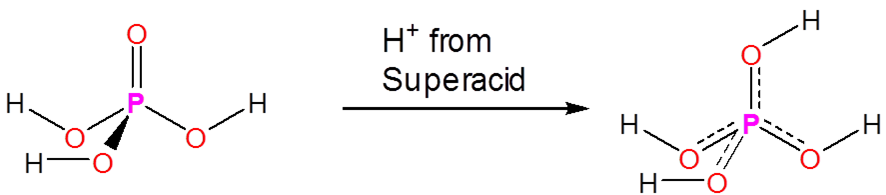
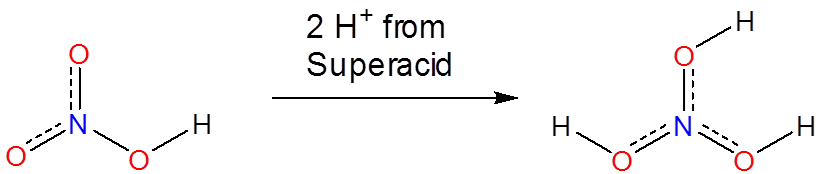
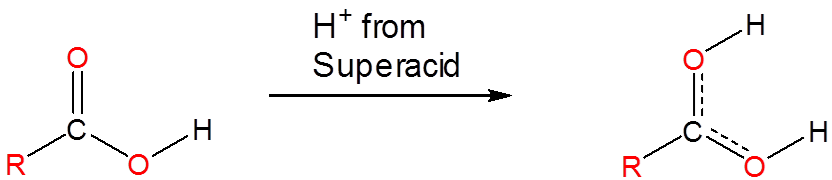
However, superacids also protonate many species that are not usually considered to have acid base properties. Even alkanes can be protonated and, in fact, superacids are used to generate carbocations in a variety of synthetic applications. They do this by protonating alkanes to give unstable species which then decompose to carbocations in further reactions. For example, mixtures of \(\ce{SbF_5}\) and \(\ce{FSO_3H}\) called Magic Acid can even protonate methane, which gives a \(\ce{CH_5^{+}}\) cation:
\[\ce{F_5Sb + FSO_3H + CH_4 -> F_5Sb-OSO_2F^{-} + CH_5^{+}} \nonumber \]
which subsequently decomposes to give an ordinary carbocation
\[\ce{CH_5^{+} -> CH_3^{+} + H_2}\nonumber \]
Since liquid superacids are extremely corrosive and can be costly to separate from reaction mixtures, solid superacids are used industrially instead. The main use for these solid superacids is to generate carbocations for use in hydrocarbon isomerization and alkylation chemistry. Many solid superacids consist of sulfuric acid/sulfates attached to a metal oxide surface to give structures similar to that shown below:
 \[]\
\[]\
These structures exhibit Hammett acidity parameters in the superacid range. However, the mechanism by which these solid superacids generate carbocations isn't entirely clear since they contain both Brønsted acid sites (at OH) and Lewis acid sites (at M) that could be involved in the carbocation generation process.
The Hammett Acidity Function
The acid ionization constants typically used to measure weak acids' acidity are only valid in dilute aqueous solutions. A more general measure of acidity that in principle is valid for any acid is the Hammett acidity function. The Hammett acidity function, \(H_o\), is analogous to the pH used to describe the acidity of aqueous solutions but instead refers to the pure acid:
\[pH = -\log(A_{\ce{H^{+}}}) \tag{for dilute aqueous solutions} \]
\[H_o = -\log (A_{\ce{H^{+}}}) \tag{for pure acids} \]
where \(\ce{A_{H^{+}}}\) is the activity of \(\ce{H^{+}}\), which in many dilute solutions is approximately equal to the hydrogen ion concentration (that is why the pH is often defined in terms of [H+].
At first glance it may seem that the Hammett acidity function is simply a generalization of the pH concept for use in nonaqueous solutions. This is especially so since in water the the pH and \(H_o\) do refer to the same quantity. However, the hydrogen ion of the Hammett acidity function is more than a generalization of the pH concept. Its real genius lies in that \(A_{H^+}\) does not necessarily represent an actual chemical species of identity \(H^+\) but rather an acid's ability to protonate weak indicator bases, B, specifically via the reaction:
\[\ce{H^{+} + B <=> BH^{+}}\nonumber \]
This reaction gives the weak acid \(BH^+\) which can ionize in the reaction that is the reverse of that above:
\[\ce{BH^{+} <=> B + H^{+}}\nonumber \]
The extent of this ionization will depend on \(A_{H^+}\) according to
\[K_{ion} = \dfrac{[\ce{BH^{+}}]}{A_{\ce{H^{+}}}[B]}\nonumber \]
Taking the negative logarithm of both sides and rearranging gives the Henderson-Hasselbach equation for the indicator base, \(\ce{B}\):
\[-K_{ion} = -\log{A_{\ce{H^{+}}}} -\log{\dfrac{[\ce{BH^{+}}]}{[\ce{B}]}}\nonumber \]
which can be rearranged to give
\[pK_{ion} = H_o -\log{\dfrac{[\ce{BH^{+}}]}{[\ce{B}]}}\nonumber \]
or
\[H_o= pK_{ion} -\log{\dfrac{[\ce{BH^{+}}]}{[\ce{B}]}}\nonumber \]
From this it is apparent that \(H_o\) represents an acid's ability to donate a hydrogen ion, as measured in terms of its ability to shift the equilibrium between \(\ce{B}\) and \(\ce{BH^{+}}\) towards \(\ce{BH^{+}}\). More negative values of \(H_o\) correspond to stronger Brønsted acids with a greater hydrogen ion transfer ability while less negative ones indicate weaker Brønsted acidity.
The value of \(H_o\) has been experimentally determined for a number of strong acids by measuring the ratio of \(\ce{BH^{+}}\) to \(\ce{B}\) using weakly basic aromatics like 2,4,6-trinitroaniline, various nitrotoluenes, and triflouromethylbenzene as the indicator base, B. Some of these Hammett acidity parameters are shown in Table \(\PageIndex{1}\).
As can be seen from table \(\PageIndex{1}\), sulfuric acid has a Hammett acidity of -12. Since superacids are defined as acids with greater Brønsted acidity than pure sulfuric acid this means that superacids have \((H_o<-12)\).
| Acid | \(H_o\) |
|---|---|
| Sulfuric acid, \(H_2SO_4\) | -12 |
| Perchloric Acid, \(HClO_4\) | -13.0 |
| Triflic acid (triflouromethanesulfonic acid), \(CF_3SO_3H\) | -14.6 |
| Flourosulfonic acid, \(FSO_3H\) | -15.6 |
| Magic Acid, \(F_5Sb---FSO_3H\) | -24 to -21\(^a\) |
| Fluoroantimonic acid, \(SbF_5---FH\) | -24 to -21\(^{a,b}\) |
a. Difficult to estimate reliably.
b. Depends on the \(SF_5\) to \(FSO_3H\) ratio.
References
- Gillespie, R. J.; T. E. Peel, T. E.; Robinson, E.A. J. Am. Chem. Soc. 1971, 93(20), 5083-5087.
- Gillespie, R. J.; T. E. Peel, T. E. J. Am. Chem. Soc., 1973, 95(16), 5173-5178.3.
- Olah, George A. Superacid chemistry, 2nd ed. Hoboken, N.J.: Wiley. 2009.

