6.3.5: Thermodynamics of Solution-Phase Brønsted Acidity and Basicity
- Page ID
- 157370
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The behavior of Brønsted-Lowry acids and bases in solution is heavily influenced by solvation
This is particularly true in aqueous systems in which the energies and entropies of hydration can be quite significant. Consider the enthalpy and entropy changes for the dissociation of a number of acids in dilute aqueous solution at 25°C as given in Table \( \PageIndex{1}\).
| Acid |
\( \Delta S^°\) (J/mol-K) |
\(-T \times \Delta S^°\) (kJ/mol) |
\( \Delta H^°\) (kJ/mol) |
\( \Delta G^°\) (kJ/mol) |
\(K_a\) (calcd. from \( \Delta G^°\) ) |
|---|---|---|---|---|---|
| HF | -102 | 30 | -16 | 14 | \(6.8 \times 10^{-4}\) |
| HCl | -35 | 10 | -57 | -47 | \(10^8\) |
| HBr | -13 | 4 | -65 | -61 | \(10^{10}\) |
| HI | 11 | -3 | -62 | -65 | \(10^{11}\) |
| HClO | -95.4 | 28.4 | 13.9 | 42.3 | \(4 \times 10^{-8}\) |
| HClO2 | -86.6 | 25.8 | -14.6 | 11.2 | \(1.1 \times 10^{-2}\) |
| H3PO4 → H+ + H2PO4- | -66.9 | 20.0 | -7.9 | 12.1 | \(7.9 \times 10^{-3}\) |
| CH3CO2H → H+ + CH3CO2- | -92.4 | 27.5 | -0.4 | 27.1 | \(1.8 \times 10^{-5}\) |
As can be seen from the data in Table \( \PageIndex{1}\), the major driving force for dissociation of inorganic acids is the enthalpy of dissociation, which is exothermic for all of the acids listed except very weakly acidic HClO. In contrast, the entropy term usually disfavors dissociation since it is negative for all acids except weakly polar HI (for which it contributes little to the overall free energy of dissociation). The situation is exactly reversed in the case of acetic acid, \(CH_3CO_2H\), for which the enthalphly of dissociation is small and the entropy is the dominant contributor to the free energy.
Further insight into the factors which govern Brønsted acid strength in aqueous solution may be gained by examining the relative contributions of heterolytic H-A bond breaking and hydration to the enthalpy of dissociation. This is done using the thermodynamic cycle depicted in Figure \(\PageIndex{1}\).
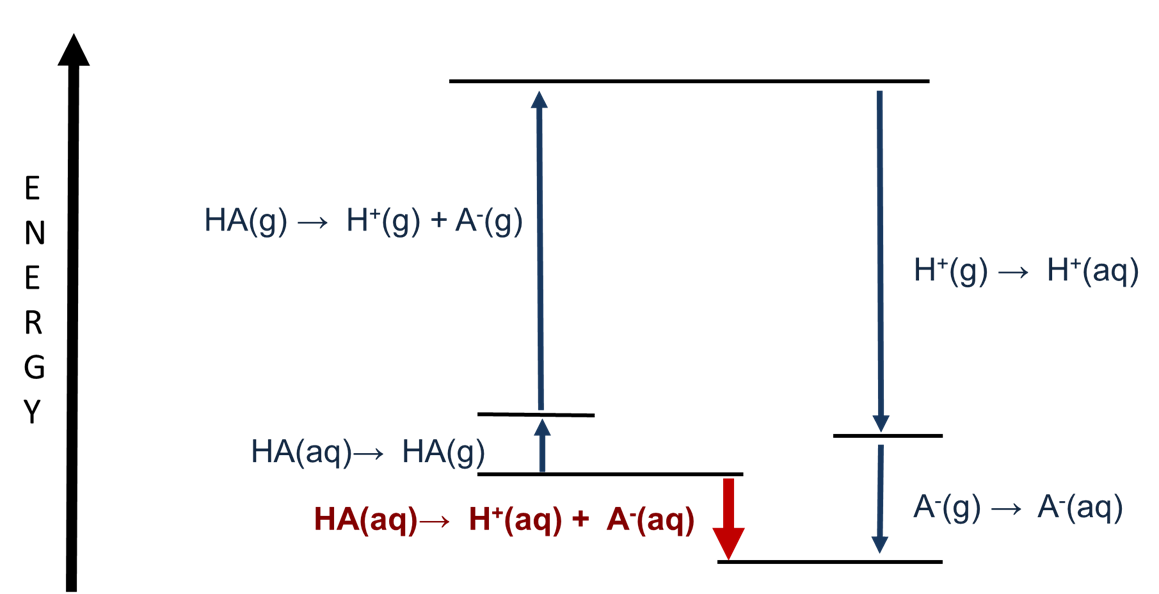
As can be seen from Figure \(\PageIndex{1}\), while most of the process involves solvation energies, the heterolytic bond dissociation enthalpy is also a major factor in determining the acid dissociation enthalpy. The heterolytic bond dissociation energy step is a gas phase Brønsted acid base reaction:
\[\ce{HA(g) → H^{+}(g) + A^{-}(g)} \nonumber \]
Consequently it will be important to consider gas phase acidity before examining the thermodynamics of acid ionization further.
References
- The data for inorganic acids is compiled from or calculated from data compiled in Dasent, W. E. Inorganic Energetics: An Introduction, 2nd ed. Cambridge University Press, 1982, pp. 168-170.
- The data for acetic acid is calculated from the data given in Meissler, G.L.; Fischer, P.J.; Tarr, D.A. Inorganic Chemistry, 5th ed. Pearson, 2014, pg. 175.

