5.4.1: Bifluoride anion
- Page ID
- 172981
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Finding SALCs and drawing the MO diagram for [F-H-F]\(^-\)
The linear anion [F-H-F]\(^-\) is a good place to start as an example to illustrate the process of generating pendant atom SALCs and then constructing a molecular orbital diagram for a polyatomic molecule. We will proceed using the steps outlined on the previous page for generating SALCs and a molecular orbital diagram.
Step 1. Find the point group of the molecule and assign Cartesian coordinates so that z is the principal axis.
We begin by assigning the appropriate point group for this molecule: \(D_{\infty h}\) (Figure \(\PageIndex{1}\)). As mentioned in the previous page, it is useful to substitute \(D_{2h}\) for \(D_{\infty h}\) when generating SALCs and molecular orbital diagrams. The \(z\) axis is assigned to be colinear with the principal axis, and in this case is the same as the \(C_\infty\) axis (Figure \(\PageIndex{1}\)).
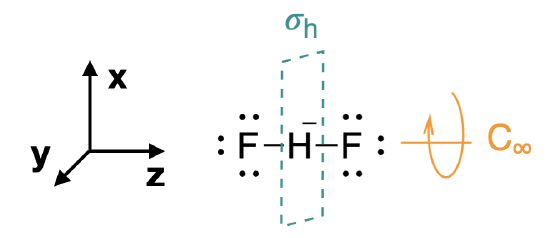
Step 2. Identify and count the pendant atoms' valence orbitals.
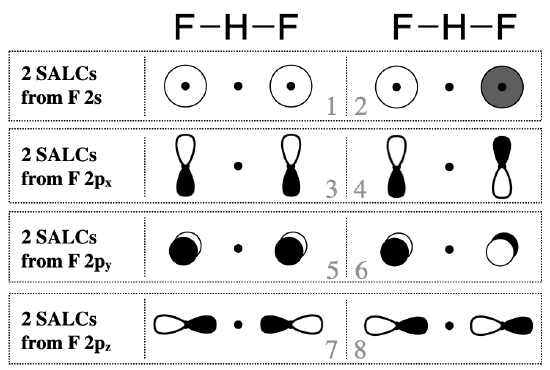
The next step is to identify the valence orbitals on the pendant F atoms that will form SALCs. In most cases, you should consider all of the valence orbitals. In this case, each of the fluorine atoms has four valence orbitals (\(2s\), \(2p_x\), \(2p_y\), and \(2p_z\)). From these eight fluorine valence orbitals, we should expect eight group orbitals (SALCs).
3. - 5. Generate SALCS (shortcut)
To draw these SALCs for this molecule is rather simple, and we don't need to follow all the steps of finding the \(\Gamma\)'s and reducing them. Rather, you can proceed as if you are creating bonding and antibonding molecular orbitals between the two F atoms, except that the F orbitals are separated by the H atom. Approximate sketches of the eight SALCs from F valence orbitals are shown in Figure \(\PageIndex{2}\).
6. Draw the MO diagram by combining SALCs with AO’s of like symmetry.
SALCs can productively interact with the central atom only when symmetry is compatible. Just some of the groups of orbitals in Figure \(\PageIndex{2}\) possess appropriate symmetry to combine with the hydrogen atom valence orbital (the H \(1s\)). In this simple case, you can decide whether orbitals have compatible symmetry by visually inspecting the shapes of the group orbitals. The F \(2p_y\) and \(2p_x\) orbitals do not have appropriate symmetry to bond to the H \(1s\) orbital because the nodes of these orbitals run through the center of the H \(1s\) orbital, thus we can eliminate all SALCs composed from F \(2p_x\) and \(2p_y\) (these are SALCs numbered 3-6 in Figure \(\PageIndex{2}\)). On the other hand, the F \(2s\) and \(2p_z\) orbitals individually do have appropriate shape and direction in space for productive interaction with an H \(1s\) orbital. However only SALCs where the entire group has appropriate symmetry will combine with H \(1s\) to produce bonding or antibonding molecular orbitals. Only the SALCs labeled with numbers 1 and 7 can combine with an \(s\) orbital in the center of the group. The ways in which these SALCs are able to combine with H \(1s\) are illustrated in Figure \(\PageIndex{3}\).

Before we assume that both SALC-1 and SALC-7 will combine with the H \(1s\) orbital, we must consider the energies of all atomic orbitals. The F \(2p_z\) orbital has a potential energy of \(-18.7\) eV (see Table 5.3.1). This is a good match for the H \(1s\) orbital (-13.6 eV). However, the F \(2s\) orbital has a much lower energy of \(-46.37\) eV and would have weak interaction with the H \(1s\).
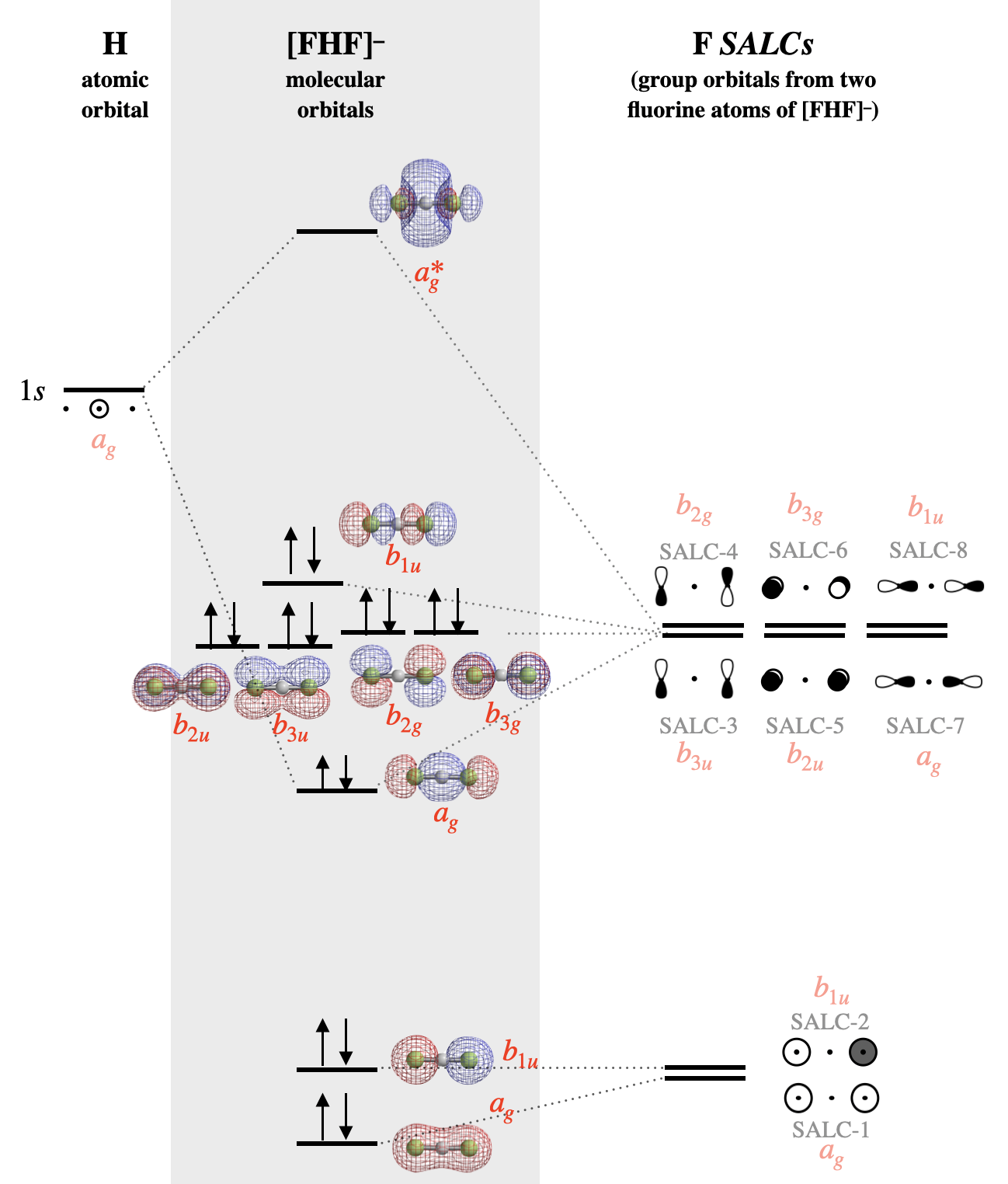
The molecular orbital diagram for [F-H-F]\(^-\) is shown in Figure \(\PageIndex{4}\). Notice that all atomic orbitals, group orbitals (SALCs), and molecular orbitals in Figure \(\PageIndex{4}\) are assigned a symmetry label that corresponds to each element's symmetry under the \(D_{2h}\) point group. The molecular orbital labels correspond to lower-case Mulliken Labels of individual reducible representations from the \(D_{2h}\) character table. Upper-case symbols are used to indicate symmetry and irreducible representations, while lower-case symbols are used to indicate the identity of an orbital with that symmetry. The labeling methods described for simple diatomic linear molecules (\(\sigma, \pi\)) are not sufficient to indicate the more complex symmetries of the molecular orbitals in polyatomic molecules. The use of lower-case Mulliken symbols is the most rigorous way to label the orbitals. Refer to your instructor for how you should label orbitals for any graded work.
- Click here for a version of Figure \(\PageIndex{4}\) using \(D_{\infty h}\) labeling:
-
For high-symmetry groups, a shortcut is to use a lower-symmetry group that maintains the critical symmetry elements. In the case of the \(D_{\infty h}\) point group, it is often sufficient to use the approximation of the \(D_{2h}\) point group and character table. This is the same MO diagram as shown above, but using the symmetry labels appropriate for the \(D_{2h}\) approximation.
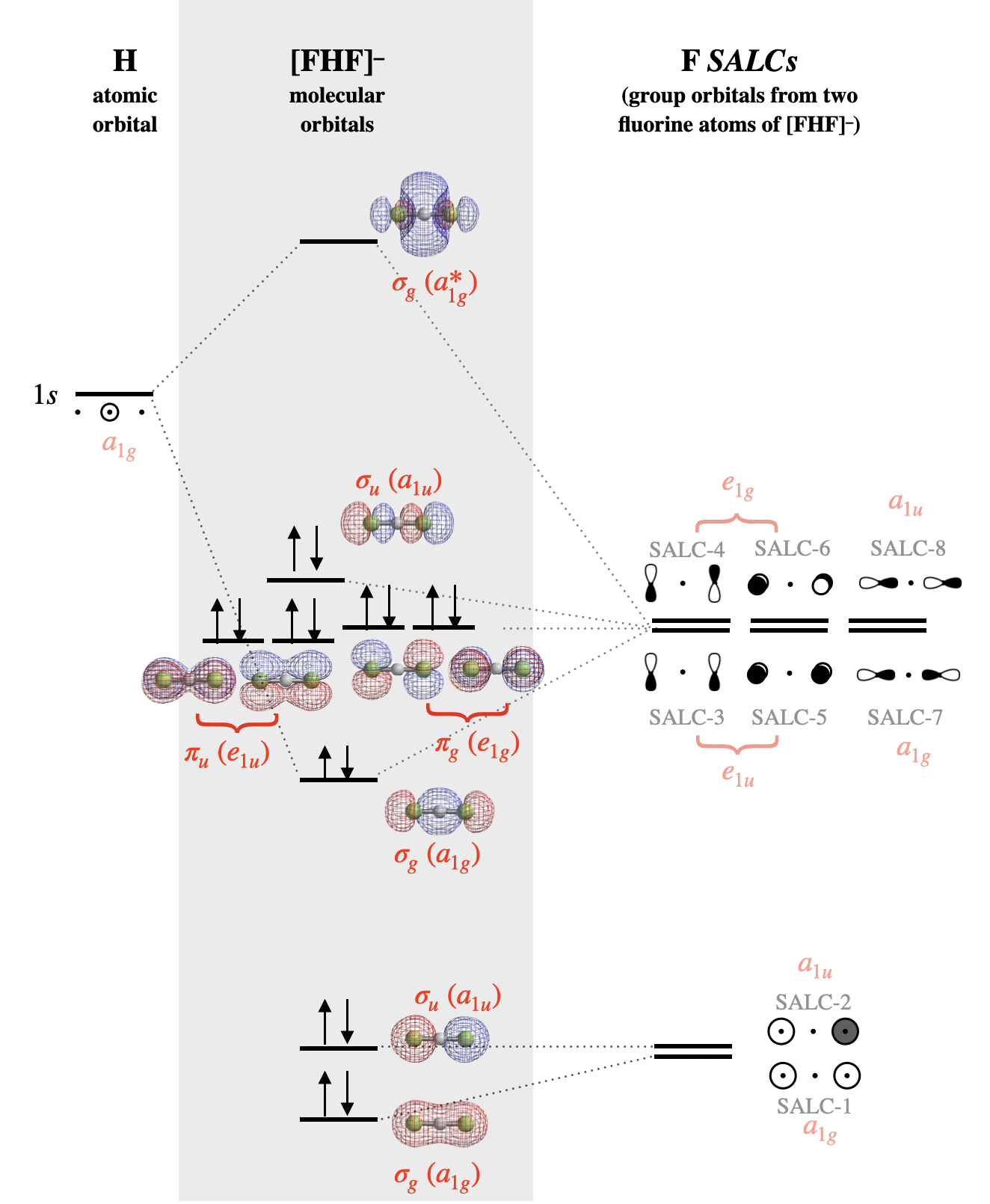
Alternate Figure \(\PageIndex{4}\): The molecular orbital diagram for [F-H-F]\(^-\). The molecular orbital surfaces and relative energy levels were calculated using Spartan software. SALCs are labeled according to numbers assigned in Figure \(\PageIndex{2}\). The symmetry of each SALC and orbital under the \(D_{2h}\) point group is shown in red font. (CC-BY-NC-SA; Kathryn Haas)
Constructing the MO diagram
After identifying the atomic orbitals and constructing SALCs, place the atomic orbitals of H on one side of the diagram and all SALCs from F on the other side. Molecular orbitals are in the center.
The lowest-energy fluorine SALCs will be those composed of the lowest-energy atomic orbitals of fluorine; these would be SALC-1 (\(a_{1g}\)) and SALC-2 (\(a_{1u}\)) that are constructed from fluorine \(s\) atomic orbitals. Of these two orbitals, the one with zero nodes would be slightly lower in energy than the one with one node. When these two orbitals form molecular orbitals, the completely symmetric SALC-1 will be mostly non-bonding with slight bonding character from minor combination with the hydrogen \(1s\) orbital. SALC-2, however is symmetrically incompatible with hydrogen \(1s\) and will be a truly non-bonding orbital distributed over both F atoms.
The six SALCs constructed of fluorine \(p\) orbitals will have higher energy since the fluorine \(p\) atomic orbitals are higher in energy than the \(s\) orbitals (SALC-3 through SALC-8). Again, we expect SALCs with more nodes (SALC-4, -6, -8) to have slightly higher energy than those with fewer nodes (SALC-3, -5, -7). SALC-7 will form a bonding and antibonding interaction with the hydrogen \(1s\) orbital. All other SALCS are truly non-bonding, but are non-degenerate non-bonding orbitals.
In bifluoride, there is an important distinction between the Lewis structure and molecular orbital description of lone pairs. In Lewis theory, the lone pairs are localized to individual fluorine atoms, while in the molecular orbital description each lone pair is distributed over both fluorine atoms at once (see surface depiction of each molecular orbital in Figure \(\PageIndex{4}\)).

