5.2.3: Diatomic Molecules of the First and Second Periods
- Page ID
- 238687
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)First Period Homonuclear Diatomic Molecules
In the first row of the periodic table, the valence atomic orbitals are \(1s\). There are two possible homonuclear diatomic molecules of the first period:
Dihydrogen, H2 \([\sigma_g^2(1s)]\): This is the simplest diatomic molecule. It has only two molecular orbitals (\(\sigma_g\) and \(\sigma_u^{*}\)), two electrons, a bond order of 1, and is diamagnetic. Its bond length is 74 pm. MO theory would lead us to expect bond order to decrease and bond length to increase if we either add or subtract one electron. The calculated bond length for the \(\ce{H_2^{+}}\) ion is approximately 105 pm.1
Dihelium, He2 \([\sigma_g^2\sigma_u^{*2}(1s)]\): This molecule has a bond order of zero due to equal number of electrons in bonding and antibonding orbitals. Like other nobel gases, He exists in the atomic form and does not form bonds at ordinary temperatures and pressures.
Draw the complete molecular orbital diagrams for \(\ce{H2}\) and for \(\ce{He2}\). Include sketches of the atomic and molecular orbitals.
- Answer
-
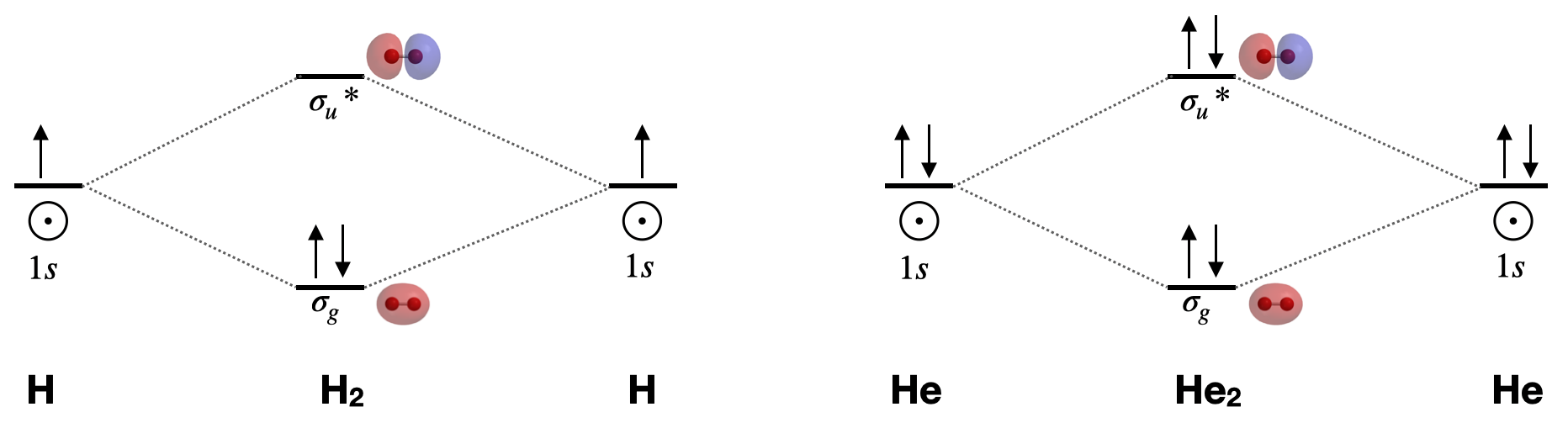
Figure for Exercise \(\PageIndex{1}\): Molecular orbital diagrams for dihydrogen and dihelium. Molecular orbital surfaces calculated using Spartan software. (CC-BY-NC-SA; Kathryn Haas) A complete molecular orbital diagram includes all atomic orbitals and molecular orbitals, their symmetry labels, and electron filling.
Second Period Homonuclear Diatomic Molecules
The second period elements span from Li to Ne. The valence orbitals are 2s and 2p. In their molecular orbital diagrams, non-valence orbitals (1s in this case) are often disregarded in molecular orbital diagrams.
Orbital mixing has significant consequences for the magnetic and spectroscopic properties of second period homonuclear diatomic molecules because it affects the order of filling of the \(\sigma_g(2p)\) and \(\pi_u(2p)\) orbitals. Early in period 2 (up to and including nitrogen), the \(\pi_u(2p)\) orbitals are lower in energy than the \(\sigma_g(2p)\) (see Figure \(\PageIndex{1})\). However, later in period 2, the \(\sigma_g(2p)\) orbitals are pulled to a lower energy. This lowering in energy of \(\sigma_g(2p)\) is not unique; all of the \(\sigma\) orbitals in the molecule are pulled to lower energy due to the increasing positive charge of the nucleus. The \(\pi\) orbitals in the molecule are also affected, but to a much lesser extent than \(\sigma\) orbitals. The reason has to do with the high penetration of \(s\) atomic orbitals compared to \(p\) atomic orbitals (recall our previous discussion on penetration and shielding, and its effect on periodic trends). The \(\sigma\) molecular orbitals have more \(s\) character and thus their energy is more influenced by increasing nuclear charge. As nuclear charge increases, the energy of the \(\sigma_g(2p)\) orbital is lowered significantly more than the energy of the \(\pi_u(2p)\) orbitals (Figure \(\PageIndex{1})\).
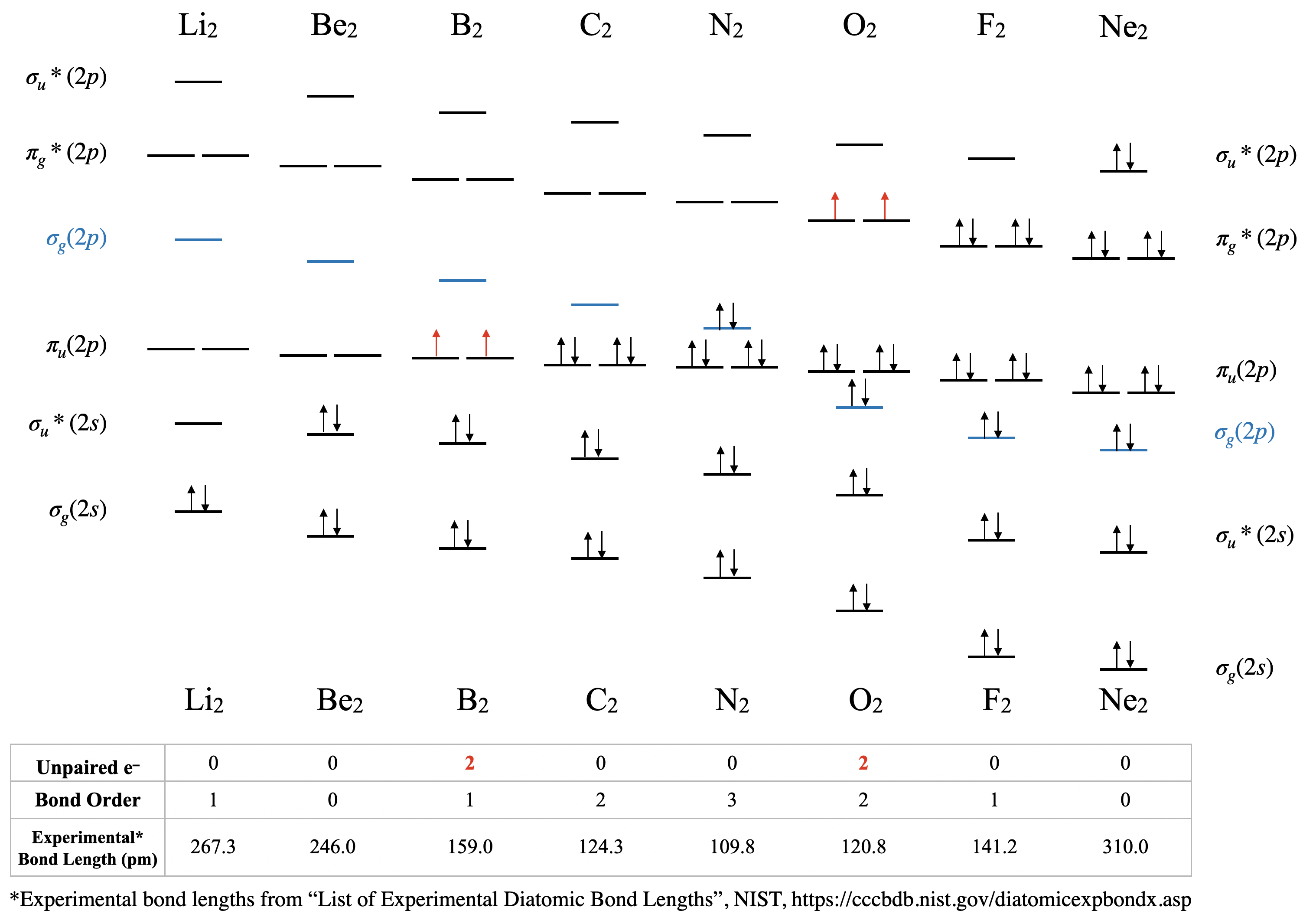
Dilithium, Li2 \([\sigma_g^2(2s)]\): This molecule has a bond order of one and is observed experimentally in the gas phase to have one Li-Li bond.
Diberylium, Be2 \([\sigma_g^2\sigma_u^{*2}(2s)]\): This molecule has a bond order of zero due to the equal number of electrons in bonding and antibonding orbitals. Although Be2 does not exist under ordinary conditions, it can be produced in a laboratory and its bond length measured (Figure \(\PageIndex{2}\)). Although the bond is very weak, its bond length is surprisingly ordinary for a covalent bond of the second period elements.2
Diboron, B2 \([\sigma_g^2\sigma_u^{*2}(2s)\pi_u^1\pi_u^1(2p)]\): The case of diboron is one that is much better described by molecular orbital theory than by Lewis structures or valence bond theory. This molecule has a bond order of one. The molecular orbital description of diboron also predicts, accurately, that diboron is paramagnetic. The paramagnetism is a consequence of orbital mixing, resulting in the \(\sigma_g\) orbital's being at a higher energy than the two degenerate \(\pi_u^*\) orbitals.
Dicarbon, C2 \([\sigma_g^2\sigma_u^{*2}(2s)\pi_u^2\pi_u^2(2p)]\): This molecule has a bond order of two. Molecular orbital theory predicts two bonds with \(\pi\) symmetry, and no \(\sigma\) bonding. C2 is rare in nature because its allotrope, diamond, is much more stable.
Dinitrogen, N2 \([\sigma_g^2\sigma_u^{*2}(2s)\pi_u^2\pi_u^2\sigma_g^2(2p)]\): This molecule is predicted to have a triple bond. This prediction is consistent with its short bond length and bond dissociation energy. The energies of the \(\sigma_g(2p)\) and \(\pi_u(2p)\) orbitals are very close, and their relative energy levels have been a subject of some debate (see next section for discussion).
Dioxygen, O2 \([\sigma_g^2\sigma_u^{*2}(2s)\sigma_g^2\pi_u^2\pi_u^2\pi_g^{*1}\pi_g^{*1}(2p)]\): This is another case where valence bond theory fails to predict actual properties. Molecular orbital theory correctly predicts that dioxygen is paramagnetic, with a bond order of two. Here, the molecular orbital diagram returns to its "normal" order of orbitals where orbital mixing could be somewhat ignored, and where \(\sigma_g(2p)\) is lower in energy than \(\pi_u(2p)\).
Difluorine, F2 \([\sigma_g^2\sigma_u^{*2}(2s)\sigma_g^2\pi_u^2\pi_u^2\pi_g^{*2}\pi_g^{*2}(2p)]\): This molecule has a bond order of one and like oxygen, the \(\sigma_g(2p)\) is lower in energy than \(\pi_u(2p)\).
Dineon, Ne2 \([\sigma_g^2\sigma_u^{*2}(2s)\sigma_g^2\pi_u^2\pi_u^2\pi_g^{*2}\pi_g^{*2}\sigma_u^{*2}(2p)]\): Like other noble gases, Ne exists in the atomic form and does not form bonds at ordinary temperatures and pressures. Like Be2, Ne2 is an unstable species that has been created in extreme laboratory conditions and its bond length has been measured (Figure \(\PageIndex{2}\))
Draw the complete molecular orbital diagram for O2. Show calculation of its bond order and tell whether it is diamagnetic or paramagnetic.
- Answer
-
O2 is paramagnetic with a bond order of 2. Its \(\sigma_g(2p)\) molecular orbital is lower in energy that the set of \(\pi_{u}(2p)\) orbitals.
Bond order \(=\frac{1}{2}\left[\left(\begin{array}{c}\text { 8 electrons in} \\ \text { valence bonding orbitals }\end{array}\right)-\left(\begin{array}{c}\text {4 electrons in} \\ \text { valence antibonding orbitals }\end{array}\right)\right]\)

Figure for Exercise \(\PageIndex{2}\). Molecular orbital diagram of O2. (CC-BY-NC-SA, Kathryn Haas)
Use a qualitative molecular orbital energy-level diagram to predict the electron configuration, the bond order, and the number of unpaired electrons in the peroxide ion (O22−).
- Answer
-
This diagram looks similar to that of \(\ce{O2}\), except that there are two additional electrons.
\( \left ( \sigma _{g}(2s) \right )^{2}\left ( \sigma_u ^{\star }(2s) \right )^{2}\left ( \sigma _g(2p) \right )^{2}\left ( \pi _{u}(2p) \right )^{4}\left ( \pi _g(2p) \right )^{4} \); bond order of 1; no unpaired electrons.
Bond Lengths in Homonuclear Diatomic Molecules
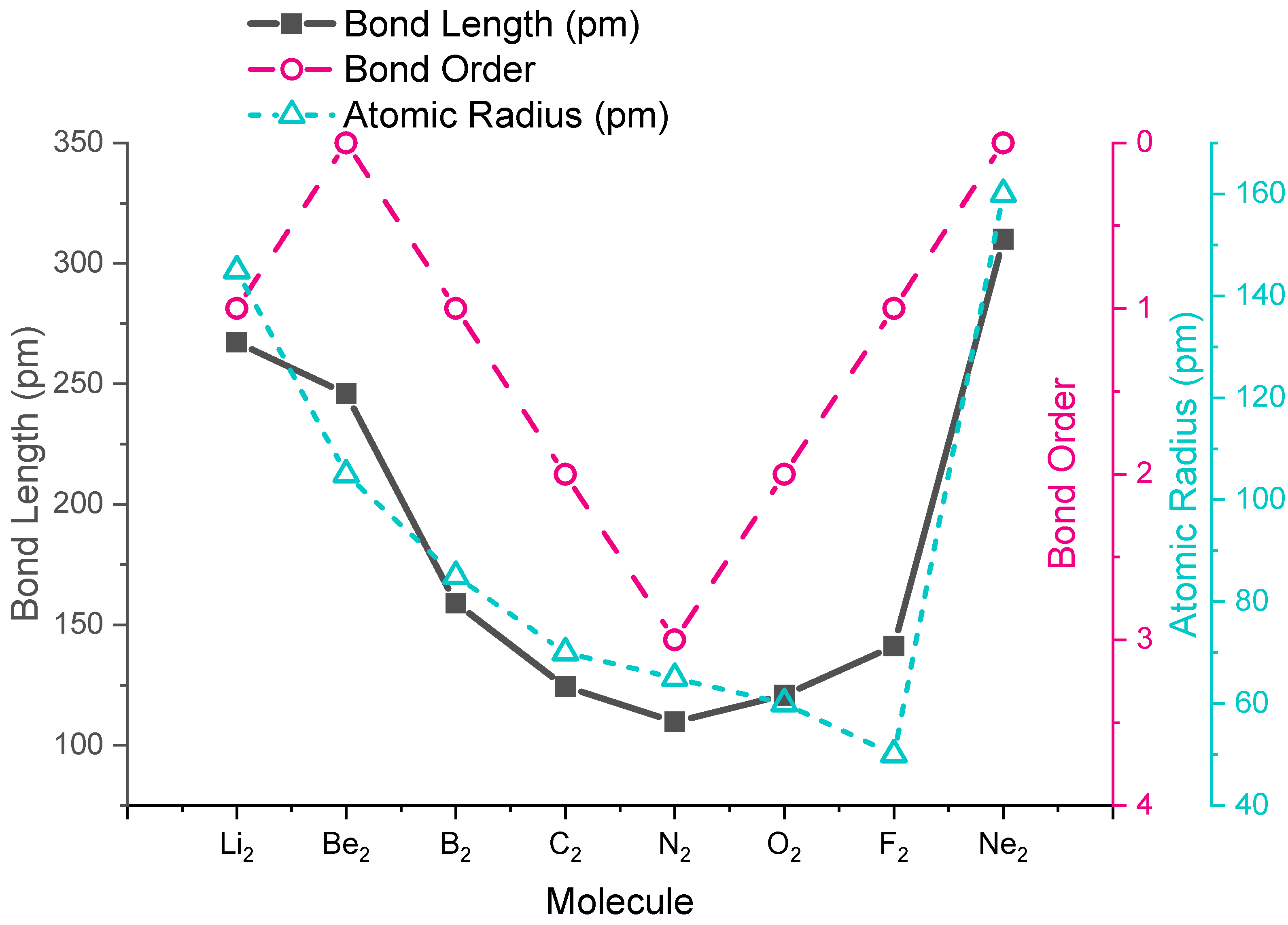
The trends in experimental bond lengths are predicted by molecular orbital theory, specifically by the calculated bond order. The values of bond order and experimental bond lengths for the second period diatomic molecules are given in Figure \(\PageIndex{1}\), and shown in graphical format on the plot in Figure \(\PageIndex{2}\). From the plot, we can see that bond length correlates well with bond order, with a minimum bond length occurring where the bond order is greatest (\(\ce{N2}\)). The shortest bond distance is at \(\ce{N2}\) due to its high bond order of 3. From \(\ce{N2}\) to \(\ce{F2}\) the bond distance increases despite the fact that atomic radius decreases.
References
- NIST, Calculated Geometries available for H2+ (Hydrogen cation) 2Σg+ D∞h, available at https://cccbdb.nist.gov/diatomicexpbondx.asp
- Merritt, J. M.; Bondybey, V. E.; Heaven, M. C., Beryllium Dimer-Caught in the Act of Bonding. Science 2009, 324 (5934), 1548-1551.


