2.2.3: Aufbau Principle
- Page ID
- 166239
Introduction
The Aufbau Principle (also called the building-up principle or the Aufbau rule) states that, in the ground state of an atom or ion, electrons fill atomic orbitals of the lowest available energy level before occupying higher-energy levels. In general, an electron will occupy an atomic orbital with the lowest value of \(n, l, m_l\), in that order of priority. The value of \(m_s\) for an unpaired electron is conventionally assigned a value of \(+\frac{1}{2}\). Each electron in an atom/ion must have a unique set of values for all four quantum numbers.
The Ground State of Hydrogenic Atoms/Ions
In a hydrogenic atom/ion, there is only one electron. In this case, the only factor determining energy is the value of \(n\). The ground state will always be the 1s orbital (\(n=1, l=0, m_l=0, m_s=+\frac{1}{2}\)).
The Ground State of Multi-electron Atoms/Ions
In atoms/ions with two or more electrons, the ground state electron configuration (1) minimizes the total energy of the electrons, (2) obeys the Pauli exclusion principle, (3) obeys Hunds rule of maximum multiplicity, and (4) considers the exchange interaction. These "rules" are described below.
| (1) Electrons will occupy the lowest energy orbitals in order to minimize the total energy. The two quantum numbers that are related to energy in multi-electron atoms are \(n\), and \(l\). Thus, orbitals with the lowest values of \(n\) and \(l\) will fill first. |

|
|
(2) Hund's rule of maximum multiplicity states that for a given electron configuration, the lowest energy arrangement of electrons in degenerate orbitals is the one with the greatest "multiplicity," where multiplicity is the number of unpaired electrons (n) plus 1 (multiplicity = n + 1). This rule is used to predict the ground state of an atom or molecule with one or more open electronic shells. Hund's rule is based on empirical observation of atomic spectra, and it is a consequence of the energy required to pair two electrons in the same orbital. This energy of repulsion between two electrons in the same orbitals is a Coulombic energy of repulsion, \(\Pi_c\), caused by two electrons with like charge sharing the same area of space (an orbital). When more than one electron occupies a set of degenerate orbitals, the most favorable arrangement is one where the number of paired electrons is minimized. A simplified definition of Hund's rule is that the lowest energy arrangement is the one with the greatest number of unpaired electrons. This implies that if two or more orbitals of equal energy are available, electrons will occupy them singly before filling them in pairs. Examples of ground state arrangements of electrons in three degenerate p-orbitals is given in the figure shown here. |
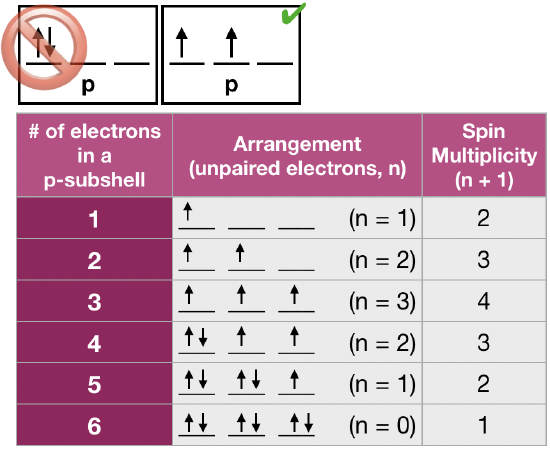 Figure \(\PageIndex{2}\). Hund's rule is that spin multiplicity must be maximized in the ground state. (Kathryn Haas; CC-NC-BY-SA) Figure \(\PageIndex{2}\). Hund's rule is that spin multiplicity must be maximized in the ground state. (Kathryn Haas; CC-NC-BY-SA) |
| (3) The Pauli exclusion principle states that it is impossible for two electrons of a multi-electron atom to have the same set of values for all four quantum numbers. Two electrons in different orbitals will have a different set of \(n, l\), and \(m_l\) values. When two electrons reside in the same orbital, they posses the same \(n, l\), and \(m_l\) values, therefore their ms must be different. Thus, two electrons in the same orbital must have opposite half-integer spin projections of \(+\frac{1}{2}\) and \(-\frac{1}{2}\). | 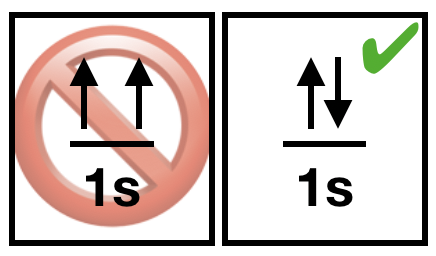 Figure \(\PageIndex{3}\). Pauli's principle tells us that paired electrons must have opposite spin. (Kathryn Haas; CC-NC-BY-SA) Figure \(\PageIndex{3}\). Pauli's principle tells us that paired electrons must have opposite spin. (Kathryn Haas; CC-NC-BY-SA) |
| (4) The exchange interaction is sometimes called the exchange energy or exchange force. However, it is not a true energy or force. Rather, it is a quantum mechanical effect that takes place between identical particles. The exchange interaction results in a ground state electron configuration with unpaired electrons all being of the same spin. Unpaired electrons are conventionally written in the "spin up" direction. | 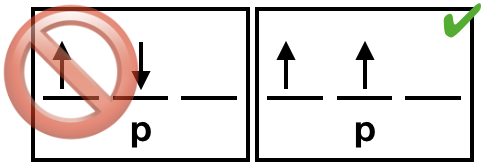 Figure \(\PageIndex{4}\). Unpaired electrons should have identical spins due to the exchange interaction. (Kathryn Haas; CC-NC-BY-SA) Figure \(\PageIndex{4}\). Unpaired electrons should have identical spins due to the exchange interaction. (Kathryn Haas; CC-NC-BY-SA) |
Trends in Expected Electron Configuration
The four "rules" above can be used as guidelines to predict the ground state electron configuration of atoms, the filling of subshells, and the configuration of electrons in degenerate orbitals. However, the utility of these guidelines for predicting actual electron configurations requires more nuanced knowledge of the relative energy levels of orbitals.
Generally, orbital energy levels directly correspond to their shell number. Additionally, orbitals within a shell generally follow the energetic trend where s<p<d<f. Although these general trends for relative orbital energy levels hold true for most of the main block elements (the s - and p-blocks), there are important exceptions in the orbital energy levels of transition metal atoms and ions of the d- and f-blocks.
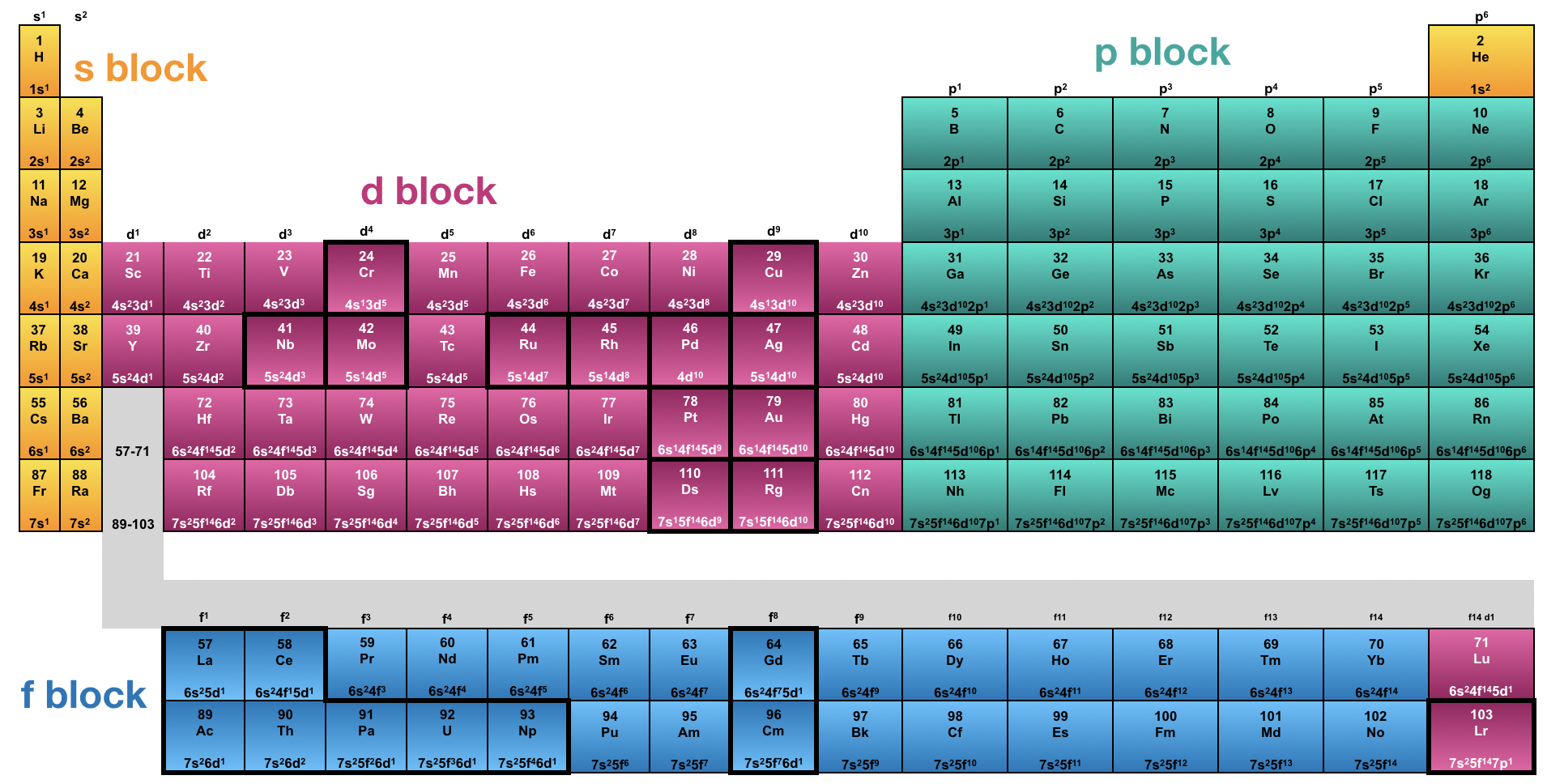
Elements that violate general trends in electron configuration are outlined with a dark line in Figure \(\PageIndex{5}\). All of the exceptions are within the d- and f- blocks, and the violations are caused by an unexpected order of the orbital energy levels.
In the next section you will learn why the orbital energy levels correlate with shell number and why subshells within a shell usually follow the trend that s<p<d<f. You will also learn why there are occasional exceptions to this trend and how these exceptions influence elemental properties.
References
- Miessler, Gary L., and Donald A. Tarr. Inorganic Chemistry. Upper Saddle River, NJ: Pearson Prentice Hall, 2010. Print.
-
Brown, Ian David. The Chemical Bond in Inorganic Chemistry the Bond Valence Model. Oxford: Oxford UP, 2006. Print.


