2.3.1: Ionization energy
- Page ID
- 198183
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ionization energy (IE) is the energy required to remove an electron from a neutral atom or cation in its gaseous phase. IE is also known as ionization potential.
\[A^{n+}_{(g)} \longrightarrow A^{(n+1)+}_{(g)} + e^- \hspace{1cm} IE = \Delta U \nonumber \]
Conceptually, ionization energy is the affinity of an element for its outermost electron (an electron it already has in its valence shell).
1st, 2nd, and 3rd Ionization Energies
The symbol \(I_1\) stands for the first ionization energy (energy required to take away an electron from a neutral atom, where \(n=0\)). The symbol \(I_2\) stands for the second ionization energy (energy required to take away an electron from an atom with a +1 charge, \(n=2\).)
- First Ionization Energy, \(I_1\) (general element, A): \[ A_{(g)} \rightarrow A^{1+}_{(g)} + e^- \nonumber\]
- Second Ionization Energy, \(I_2\) (general element, A): \[ A^{1+}_{(g)} \rightarrow A^{2+}_{(g)} + e^- \nonumber\]
- Third Ionization Energy, \(I_3\) (general element, A): \[ A^{2+}_{(g)} \rightarrow A^{3+}_{(g)} + e^- \nonumber\]
Each succeeding ionization energy is larger than the preceding energy. This means that \(I_1 < I_2 < I_3 < ... < I_n\) will always be true. For example, ionization energy increases as succeeding electrons are taken away from \(\ce{Mg}\).
\[ Mg \,_{(g)} \rightarrow Mg^+\,_{(g)} + e^- \;\;\; I_1= 738\, kJ/mol \nonumber \]
\[Mg^+ \,_{(g)} \rightarrow Mg^{2+}\,_{(g)} + e^- \;\;\; I_2= 1451\, kJ/mol \nonumber \]
Ionization energy is correlated with the strength of attraction between the positively-charged nucleus and the negatively-charged valence electrons. The higher the ionization energy, the stronger the attractive force between nucleus and valence electrons, and the more energy is required to remove a valence electron. The lower the ionization energy, the weaker the attractive force between nucleus and valence electrons, and the less energy required to remove a valence electron.
General periodic trends in electron affinity
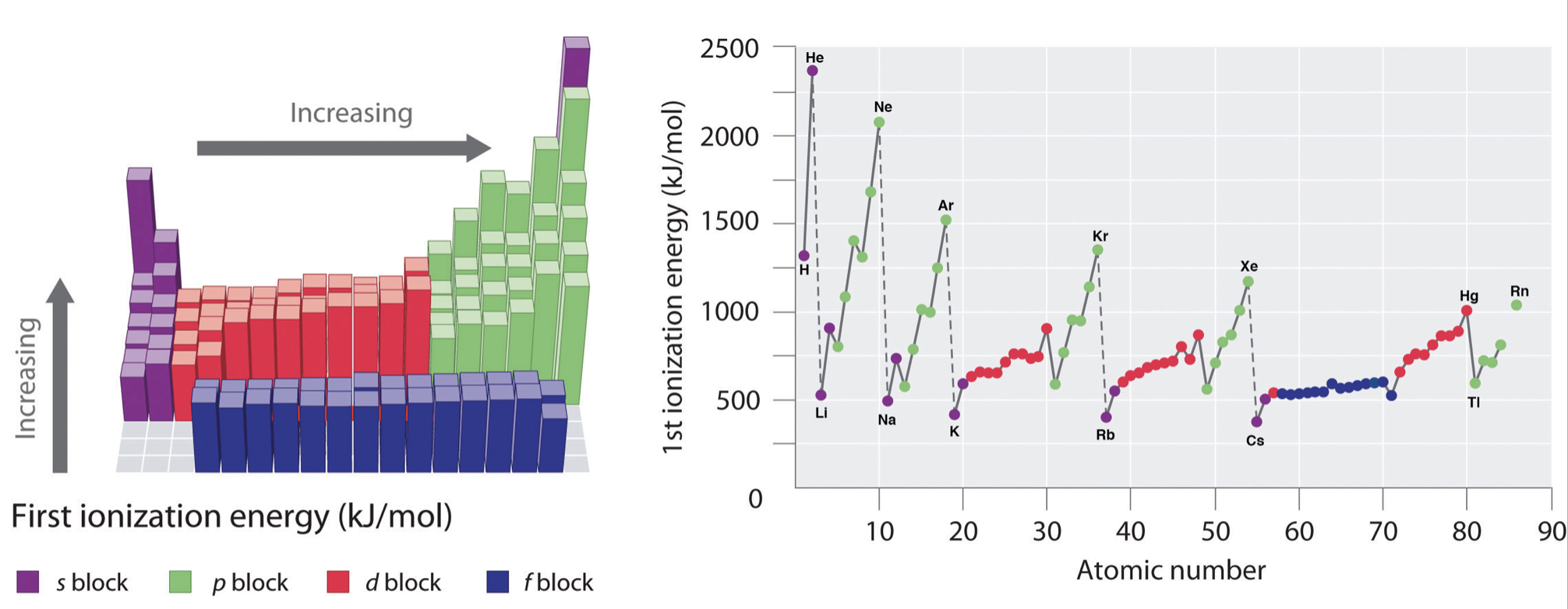
In general, ionization energies increase from left to right and decrease down a group; however, there are variations in these trends that would be expected from the effects of penetration and shielding. The trends in first ionization energy are shown in Figure \(\PageIndex{1}\) and are summarized below.
- Across a period: As Z* increases across a period, the ionization energy of the elements generally increases from left to right. However there are breaks or variation in the trends in the following cases:
- IE is especially low when removal of an electron creates a newly empty p subshell (examples include \(I_1\) of B, Al, Sc)
- IE energy is especially low where removal of an electron results in a half-filled p or d subshell (examples include \(I_1\) of O, S)
- IE increases more gradually across the d- and f-subshells compared to s- and p- subshells. This is because d- and f- electrons are weakly penetrating and experience especially low Z*.
- From one period to the next: There is an especially large decrease in IE with the start of every new period (from He to Li or from Ne to Na for example). This is consistent with the idea that IE is especially low when removal of an electron creates a newly empty s-subshell.
- Noble gases: The noble gases posses very high ionization energies. Note that helium has the highest ionization energy of all the elements.
- Down a group: Although Z* increases going down a group, there is no reliable trend in IE going down any group; in some cases IE increases going down a group, while in other cases IE decreases going down a group.
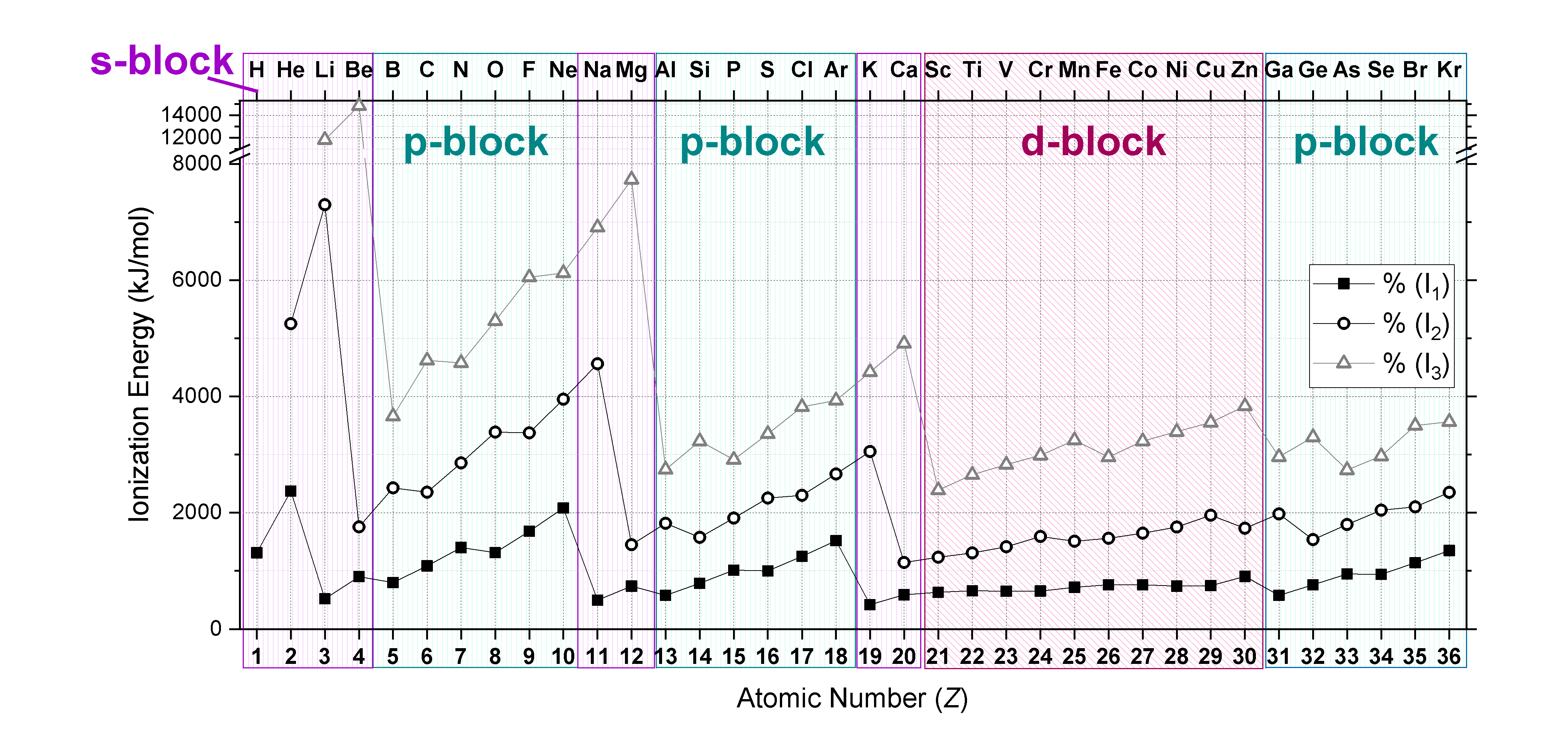
Plots of the \(I_1, I_2,\) and \(I_3\) of elements from hydrogen to krypton (first four periods) are shown in Figure \(\PageIndex{2}\). Notice that \(I_3>I_2>I_1\). Also notice that trends mentioned above for \(I_1\) hold true for subsequent ionizations when electron configurations are considered!